Three-Phase Half-Wave Uncontrolled Rectifiers

AC to DC Conversion in Power Electronics

Introduction to Rectifiers

What is Rectification?

Definition

Rectification converts alternating current (AC) to direct current (DC) using semiconductor devices such as diodes or thyristors.

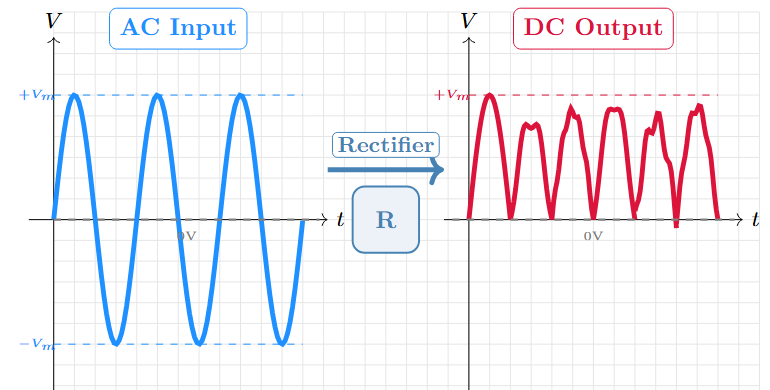
Rectification of AC to DC waveform
Rectification of AC to DC waveform

  • Essential component in DC power supplies

  • Used in applications requiring DC power from AC mains

Types of Rectifiers and Need for Three-Phases

Types of Rectifiers

  • Uncontrolled: Diodes only (fixed output)

  • Controlled: Thyristors/SCRs (variable output)

  • Half-Wave: Uses one half of AC cycle

  • Full-Wave: Uses both halves of AC cycle

Why Three-Phase?

  • Higher power capability

  • Smoother DC output (lower ripple)

  • Common in industrial applications

  • Better transformer utilization

Three-Phase System Advantages

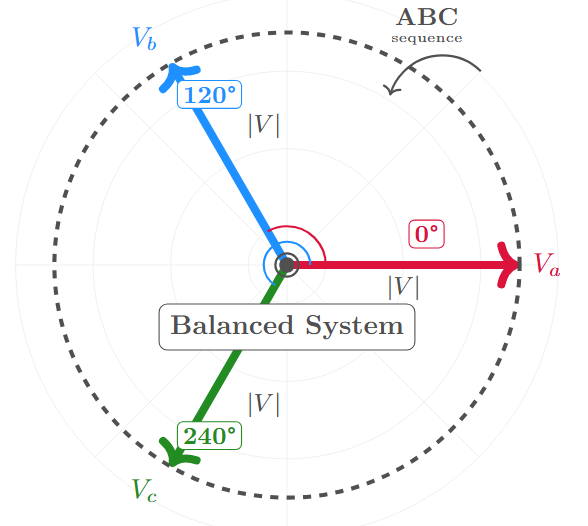
Three-phase balanced phasor diagram
Three-phase balanced phasor diagram

Benefits:

  • Constant power flow

  • Balanced system

  • Higher efficiency

  • Reduced harmonics

  • Better regulation

Key Insight

Three-phase systems provide approximately \(\sqrt{3}\) times more power than single-phase for the same conductor material, making them ideal for industrial applications.

Why Three-Phase Rectifiers?

Advantages over Single-Phase:

  • Better transformer utilization factor

  • Lower ripple factor in output

  • Higher power handling capability

  • Better efficiency

  • Reduced harmonic content

Applications:

  • High-power DC motor drives

  • Battery chargers for large systems

  • DC power supplies for industrial applications

  • Electroplating and electrochemical processes

Three-Phase Half-Wave Uncontrolled Rectifier

Circuit Configuration

Basic Circuit Components:

  • Three-phase transformer (star-connected secondary)

  • Three diodes (one per phase)

  • Load resistance \(R\)

  • Common neutral point required

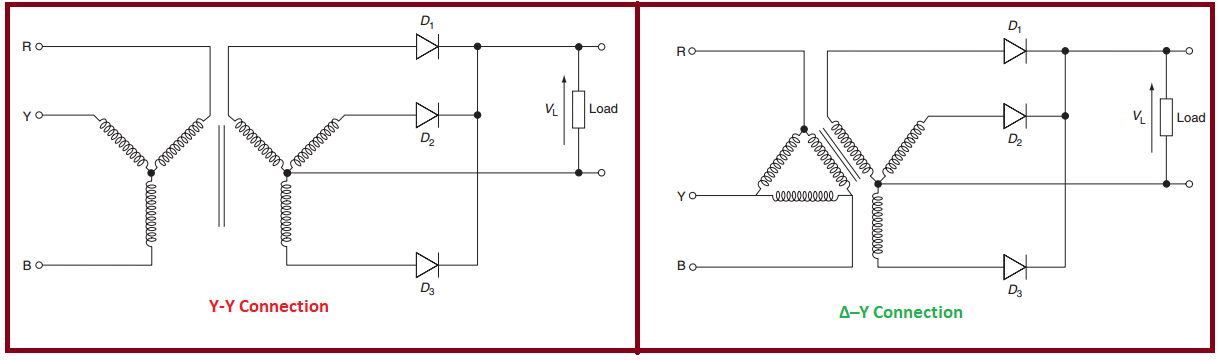
Three-phase half-wave uncontrolled rectifier circuit diagram
Three-phase half-wave uncontrolled rectifier circuit diagram

Key Features:

  • Simplest three-phase rectifier configuration

  • Uses only three diodes

  • Natural commutation

  • Unidirectional current flow

Circuit Operation Principle

Operating Principle:

  • At any instant, the diode connected to the most positive phase conducts

  • Only one diode conducts at a time

  • Current flows through the conducting diode and load

  • Non-conducting diodes are reverse-biased

Conduction Sequence:

  • Phase R: \(30^{\circ} \leq \omega t \leq 150^{\circ}\)

  • Phase Y: \(150^{\circ} \leq \omega t \leq 270^{\circ}\)

  • Phase B: \(270^{\circ} \leq \omega t \leq 390^{\circ}\) (next cycle)

Each diode conducts for \(120^{\circ}\) in each cycle.

Voltage and Current Waveforms

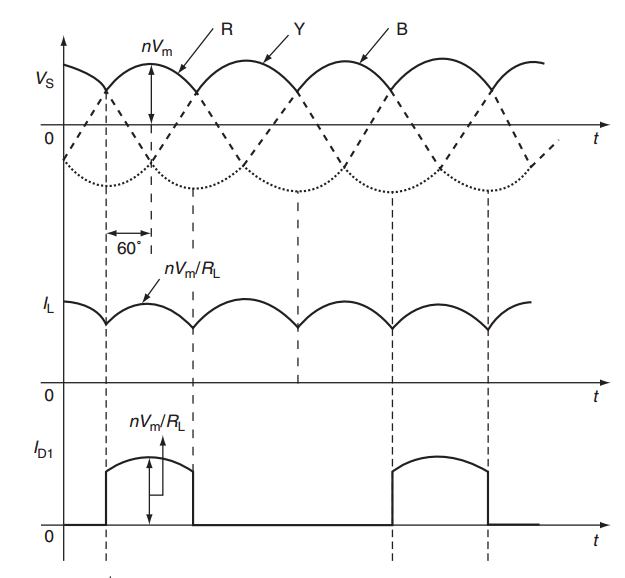
Load voltage and current waveforms for half-wave rectifier configurations
Load voltage and current waveforms for half-wave rectifier configurations

Key Observations:

  • Output voltage is pulsating DC

  • Three pulses per cycle (ripple frequency = \(3f\))

  • Continuous current through load (for resistive load)

Mathematical Analysis

Input Phase Voltages

For a balanced three-phase system with star-connected secondary:

\[\begin{aligned} v_R &= V_m n(\omega t) \\ v_Y &= V_m n(\omega t - 120^{\circ}) \\ v_B &= V_m n(\omega t - 240^{\circ}) = V_m n(\omega t + 120^{\circ}) \end{aligned}\]

Where:

  • \(V_m\): Peak value of phase voltage

  • \(\omega\): Angular frequency ( \(2\pi f\))

  • \(f\): Supply frequency

RMS Phase Voltage:

\[V_{ph} = \frac{V_m}{\sqrt{2}}\]

Output Voltage Analysis

The output voltage \(v_o\) follows the most positive input voltage:

\[\text{For } 30^{\circ} \leq \omega t \leq 150^{\circ}: \quad v_o = v_R = V_m n(\omega t)\]

Average Output Voltage:

\[V_{dc} = \frac{3}{2\pi} \int_{30^{\circ}}^{150^{\circ}} V_m n(\omega t) \, d(\omega t)\]
\[V_{dc} = \frac{3V_m}{2\pi} \left[ -\cos(\omega t) \right]_{30^{\circ}}^{150^{\circ}}\]
\[V_{dc} = \frac{3V_m}{2\pi} \left[ -\cos(150^{\circ}) + \cos(30^{\circ}) \right]\]
\[V_{dc} = \frac{3V_m}{2\pi} \left[ \frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} \right] = \frac{3\sqrt{3}V_m}{2\pi}\]

Average Output Voltage (continued)

Since \(V_m = \sqrt{2} V_{ph}\), where \(V_{ph}\) is the RMS phase voltage:

\[V_{dc} = \frac{3\sqrt{3}}{2\pi} \times \sqrt{2} V_{ph} = \frac{3\sqrt{6}}{2\pi} V_{ph} \approx 1.654 V_{ph}\]

For line voltage \(V_L = \sqrt{3} V_{ph}\) (star connection):

\[V_{dc} = \frac{3\sqrt{6}}{2\pi\sqrt{3}} V_L = \frac{3\sqrt{2}}{2\pi} V_L \approx 0.675 V_L\]

Alternative Expression:

\[V_{dc} = \frac{3\sqrt{3}V_m}{2\pi} \approx 0.827 V_m\]

RMS Output Voltage

The RMS value of output voltage:

\[V_{rms}^2 = \frac{3}{2\pi} \int_{30^{\circ}}^{150^{\circ}} V_m^2 n^2(\omega t) \, d(\omega t)\]

Using the identity \(n^2(\omega t) = \frac{1 - \cos(2\omega t)}{2}\):

\[V_{rms}^2 = \frac{3V_m^2}{4\pi} \int_{30^{\circ}}^{150^{\circ}} [1 - \cos(2\omega t)] \, d(\omega t)\]

After integration:

\[V_{rms} = V_m \sqrt{\frac{3}{4\pi} \left[ 120^{\circ} - \frac{n(300^{\circ}) - n(60^{\circ})}{2} \right]}\]
\[V_{rms} = V_m \sqrt{\frac{3}{4\pi} \left[ \frac{2\pi}{3} + \frac{\sqrt{3}}{2} \right]} \approx 0.84 V_m\]

Load Current Analysis

For resistive load \(R\):

Average Load Current:

\[I_{dc} = \frac{V_{dc}}{R} = \frac{3\sqrt{3}V_m}{2\pi R} \approx \frac{0.827 V_m}{R}\]

RMS Load Current:

\[I_{rms} = \frac{V_{rms}}{R} \approx \frac{0.84 V_m}{R}\]

Peak Load Current:

\[I_m = \frac{V_m}{R}\]

Average Diode Current:

\[I_{D(avg)} = \frac{I_{dc}}{3} = \frac{V_{dc}}{3R}\]

Performance Parameters

Ripple Factor

Ripple factor quantifies the AC content in DC output:

\[RF = \frac{V_{ac}}{V_{dc}} = \sqrt{\left( \frac{V_{rms}}{V_{dc}} \right)^2 - 1}\]

For three-phase half-wave rectifier:

\[RF = \sqrt{\left( \frac{0.84}{0.827} \right)^2 - 1} = \sqrt{(1.016)^2 - 1} \approx 0.183\]

Therefore, \(RF \approx 18.3\%\)

This is significantly lower than single-phase rectifiers (\(RF = 121\%\) for half-wave).

Form Factor and Peak Factor

Form Factor (FF):

\[FF = \frac{V_{rms}}{V_{dc}} = \frac{0.84}{0.827} \approx 1.016\]

Peak Factor (Crest Factor):

\[CF = \frac{V_m}{V_{rms}} = \frac{V_m}{0.84 V_m} \approx 1.19\]

Comparison with Ideal DC:

  • Ideal DC: \(FF = 1\), \(CF = 1\)

  • Three-phase half-wave: \(FF = 1.016\), \(CF = 1.19\)

  • Indicates very good DC characteristics

Transformer Utilization Factor

TUF measures how effectively the transformer is utilized:

\[TUF = \frac{P_{dc}}{VA \text{ rating of transformer}}\]

For three-phase half-wave rectifier:

\[P_{dc} = V_{dc} \times I_{dc}\]
\[VA_{rating} = 3 \times V_{ph} \times I_{ph(rms)}\]

Where \(I_{ph(rms)} = \frac{I_{rms}}{\sqrt{3}}\) (since each phase conducts for 120°)

\[TUF = \frac{V_{dc} \times I_{dc}}{3 \times V_{ph} \times \frac{I_{rms}}{\sqrt{3}}} = \frac{\sqrt{3} V_{dc}}{3 V_{ph}} \times \frac{I_{dc}}{I_{rms}}\]
\[TUF \approx 0.675\]

Efficiency

Rectification Efficiency:

\[\eta = \frac{P_{dc}}{P_{ac}} = \frac{V_{dc}^2/R}{V_{rms}^2/R} = \left( \frac{V_{dc}}{V_{rms}} \right)^2\]
\[\eta = \left( \frac{0.827}{0.84} \right)^2 \approx 0.969 \text{ or } 96.9\%\]

Contributing Factors:

  • No power loss in ideal diodes

  • Purely resistive load

  • Good waveform quality

Practical Considerations:

  • Diode forward voltage drop reduces efficiency

  • Transformer losses

  • Winding resistance

Practical Considerations

Diode Selection Criteria

Peak Inverse Voltage (PIV): Maximum reverse voltage across non-conducting diode occurs when one phase is at positive peak and others are at negative peaks.

\[PIV = V_m + \frac{V_m}{2} = \frac{3V_m}{2} = 1.5 V_m\]

In terms of line voltage: \(PIV = \frac{3}{\sqrt{2}} V_{ph} = \frac{3\sqrt{2}}{2} V_{ph} \approx 2.12 V_{ph}\)

Average Forward Current:

\[I_{F(avg)} = \frac{I_{dc}}{3}\]

RMS Forward Current:

\[I_{F(rms)} = \frac{I_{rms}}{\sqrt{3}}\]

Transformer Design Considerations

Secondary Winding:

  • Must be star-connected for neutral point

  • Each phase carries current for \(120^{\circ}\) per cycle

  • RMS current in each phase: \(I_{ph} = \frac{I_{rms}}{\sqrt{3}}\)

Primary Winding:

  • Can be star or delta connected

  • Carries discontinuous current

  • Contains harmonics due to non-sinusoidal secondary current

Transformer Rating:

\[S_{transformer} = 3 \times V_{ph} \times I_{ph(rms)} = 3 \times V_{ph} \times \frac{I_{rms}}{\sqrt{3}} = \sqrt{3} V_{ph} I_{rms}\]

Harmonic Analysis

The output voltage contains harmonics at frequencies \(3nf\) (where \(n = 1, 2, 3, \dots\)):

Fourier Series:

\[v_o(t) = V_{dc} + \sum_{n=1}^{\infty} V_n \cos(3n\omega t + \phi_n)\]

Dominant Harmonics:

  • 3rd harmonic (150Hz for 50Hz supply)

  • 6th harmonic (300Hz for 50Hz supply)

  • 9th harmonic (450Hz for 50Hz supply)

Filtering Requirements:

  • Low-pass filter with cutoff below 150Hz

  • Inductor-capacitor (LC) filters commonly used

  • Filter design based on acceptable ripple level

Load Types and Effects

Resistive Load (R):

  • Continuous current flow

  • Current waveform follows voltage waveform

  • Simple analysis

Inductive Load (R-L):

  • Current more continuous

  • Reduced ripple in current

  • Freewheeling diodes may be needed

  • Complex analysis required

Capacitive Load (R-C):

  • Capacitor provides filtering action

  • Discontinuous diode currents

  • Higher peak currents

  • Better voltage regulation

Advantages and Disadvantages

Advantages

  • Simple Circuit: Only three diodes required

  • Low Ripple: 18.3% vs 121% for single-phase

  • High Efficiency: Theoretical efficiency of 96.9%

  • Good TUF: Better transformer utilization than single-phase

  • Natural Commutation: No external switching control needed

  • Cost Effective: Fewer components than full-wave rectifiers

  • Reliable: Simple design enhances reliability

Disadvantages

  • Neutral Point Required: Transformer secondary must be star-connected

  • Transformer Utilization: TUF could be better

  • Unbalanced Transformer: Secondary neutral carries current

  • PIV Rating: Diodes need reasonable reverse voltage rating

  • Harmonics: Input current contains harmonics

  • Limited Power: Lower power capability than full-wave

  • DC Magnetization: Transformer core may saturate due to DC component

Applications

Typical Applications

Industrial Applications:

  • Battery charging systems

  • DC motor drives (low to medium power)

  • Electroplating processes

  • DC welding power supplies

Commercial Applications:

  • UPS systems (charging circuit)

  • LED lighting drivers

  • Telecommunications power supplies

  • Electric vehicle charging stations

Laboratory Applications:

  • Variable DC power supplies

  • Electronic equipment testing

  • Research and development projects

Design Example

Design Problem: Design a three-phase half-wave rectifier with:

  • Input: 3-phase, 415V line voltage, 50Hz

  • Output: 200V DC, 10A DC current

  • Load: Resistive

Solution Steps:

  1. Calculate required transformer secondary line voltage

  2. Determine diode ratings (PIV, current)

  3. Calculate transformer ratings

  4. Design output filter (if required)

  5. Verify performance parameters

Design Example - Solution

Given: \(V_L = {415}{\mathrm{V}}\), \(V_{dc} = {200}{\mathrm{V}}\), \(I_{dc} = {10}{\mathrm{A}}\)

Step 1: Check if given line voltage is suitable

\[V_{dc} = 0.675 \times V_L = 0.675 \times 415 \approx {280}{\mathrm{V}}\]
This is too high! A step-down transformer is needed.

Required Secondary Line Voltage:

\[V_{L(sec)} = \frac{V_{dc}}{0.675} = \frac{200}{0.675} \approx {296}{\mathrm{V}}\]

Step 2: Transformer turns ratio

\[n = \frac{V_{L(pri)}}{V_{L(sec)}} = \frac{415}{296} \approx 1.40\]

Step 3: Diode ratings

  • Average forward current: \(I_{F(avg)} = \frac{I_{dc}}{3} = \frac{10}{3} \approx {3.33}{\mathrm{A}}\)

  • Phase voltage: \(V_{ph} = \frac{296}{\sqrt{3}} \approx {171}{\mathrm{V}}\)

  • Peak inverse voltage: \(PIV = 2.12 \times 171 \approx {362}{\mathrm{V}}\)

  • Select diodes: \(I_F \geq {5}{\mathrm{A}}\), \(V_R \geq {400}{\mathrm{V}}\)

Step 4: Load resistance

\[R = \frac{V_{dc}}{I_{dc}} = \frac{200}{10} = {20}{\Omega}\]

Step 5: Performance verification

  • Ripple factor: 18.3%

  • Efficiency: 96.9%

  • Form factor: 1.016

Comparison with Other Rectifiers

Comparison Table

Comparison of rectifier types
Parameter 1-\(\phi\) Half 3-\(\phi\) Half 3-\(\phi\) Full
No. of diodes 1 3 6
Ripple factor (%) 121 18.3 4.2
Efficiency (%) 40.6 96.9 99.5
TUF 0.287 0.675 0.955
PIV \(V_m\) \(1.5 V_m\) \(V_m\)
\(V_{dc}/V_m\) 0.318 0.827 0.955
Transformer neutral Not required Required Not required

Key Observations:

  • Three-phase half-wave significantly outperforms single-phase

  • Three-phase full-wave offers better performance but at higher cost

  • Choice depends on application requirements and cost constraints

Conclusion

Summary

Key Points Covered:

  • Circuit configuration and operation principle

  • Mathematical analysis of voltages and currents

  • Performance parameters (ripple factor, efficiency, TUF)

  • Practical design considerations

  • Advantages and disadvantages

  • Applications and design example

Learning Outcomes:

  • Understand three-phase rectification principles

  • Analyze and design three-phase half-wave rectifiers

  • Evaluate performance parameters

  • Apply to practical scenarios