Single-phase half-wave rectifier with RLE load

Single-Phase Diode Rectifier with RE-Load

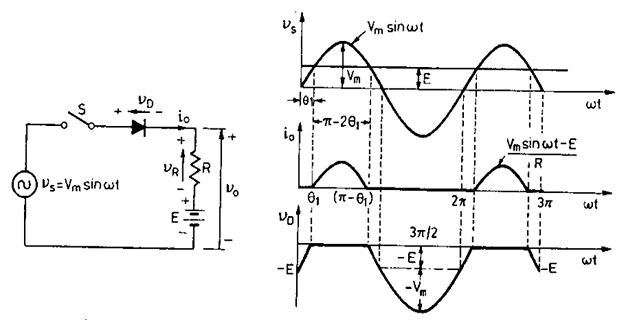
• After closing the switch, the diode is reverse biased (not conduct) until source voltage \(v_s\) equals the load counter emf \(E\)

• \[\theta_1 = \sin^{-1}\left(\dfrac{E}{V_m}\right)\]
  is given by , diode starts conducting and the turn-on angle When

• The diode conducts from \(\omega t = \theta_1\) to \(\omega t = (\pi-\theta_1)\) i.e. conduction angle for diode is \((\pi-2\theta_1)\)

• \[\begin{aligned}V_{m}\sin\omega t&=E+i_{0}R\\i_{0}&=\frac{V_{m}\sin\omega t-E}{R}\end{aligned}\]
  During diode conduction period:
• \[\begin{aligned} I_0 & =\frac{1}{2 \pi R}\left[\int_{\theta_1}^{\pi-\theta_1}\left(V_m \sin \omega t-E\right) d(\omega t)\right] \\ & =\frac{1}{2 \pi R}\left[2 V_m \cos \theta_1-E\left(\pi-2 \theta_1\right)\right] \end{aligned}\]
  Average value of this current is given by

• \[\begin{aligned} I_{o r} & =\left[\frac{1}{2 \pi} \int_{\theta_1}^{\pi-\theta_1}\left(\frac{V_m \sin \omega t-E}{R}\right) \cdot d(\omega t)\right]^{1 / 2} \\ & =\left[\frac{1}{2 \pi R^2} \int_{\theta_1}^{\pi-\theta_1}\left(V_m^2 \sin ^2 \omega t+E^2-2 V_m E \sin \omega t\right) d(\omega t)\right]^{1 / 2} \\ & =\left[\frac{1}{2 \pi R^2}\left\{\left(V_s^2+E^2\right)\left(\pi-2 \theta_1\right)+V_s^2 \sin 2 \theta_1-4 V_m E \cos \theta_1\right\}\right]^{1 / 2} \end{aligned}\]
  Rms value of the load current is
• \[P =E I_0+I_{o r}^2 R \text { watts }\]
  Power delivered to load,

• \[\begin{aligned} & =\frac{\text { Power delivered to load }}{\text { (Source voltage) (rms value of source current) }} \\ & =\frac{E I_0+I_{o r}^2 R}{V_s \cdot I_{o r}} \end{aligned}\]
  Supply pf
• \[\begin{aligned} \omega t = 0 & \quad v_D = -E \\ \omega t = \theta_1 & \quad v_D = 0 \\ \text{period diode conducts} & \quad v_D = 0 \\ \omega t = 3\pi/2 & \quad v_s = -V_m, ~~ v_D = -(V_m+E) \\ \end{aligned}\]
  Diode voltage:

• Thus, PIV for diode is \((V_m+E)\)

Single-Phase Diode Rectifier with RL-Load

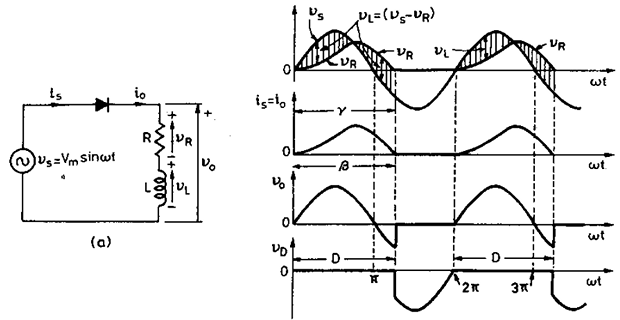
• Current \(i_o\) continues to flow even after source voltage \(v_s\) has become negative, because of the presence of \(L\) in the load.

• Inductor voltage \(v_L = v_s-v_R\), where \(v_R=i_oR\).

• \(i_o\) flows till the area \(A\) representing the energy stored by \(L\) is equal to area \(B\) representing energy released by \(L\).

• \[\begin{aligned} V_m\sin(\omega t) &=Ri(t)+L\frac{di(t)}{dt} \quad \text{for forced response}\\ 0 & =Ri(t)+L\frac{di(t)}{dt} \quad \text{for natural response} \end{aligned}\]
  Applying KVL equation:
• \[\begin{aligned} i(t) &= i_f(t)+i_n(t) \\ & = \text{Forced response} + \text{Natural response}\\ i_f(t) &=\frac{V_m}{Z}\sin(\omega t-\theta)\\ \mathrm{where}\quad Z &=\sqrt{R^2+(\omega L)^2}\quad\mathrm{and}\quad\theta=\tan^{-1}\biggl(\frac{\omega L}{R}\biggr) \\ i_n(t) & =Ae^{-t/\tau} \\ \end{aligned}\]
  Solution:

• \[i(t)=i_f(t)+i_n(t)=\frac{V_m}{Z}\sin(\omega t-\theta)+Ae^{-t/\tau}\]
  Total response:
• \[\begin{aligned} i(0) & =\frac{V_{m}}{Z}\sin(0-\theta)+Ae^{0}=0\\ A & =-\frac{V_{m}}{Z}\sin(-\theta)=\frac{V_{m}}{Z}\sin\theta \end{aligned}\]
  Using initial condition to evaluate
• \[\begin{gathered} i(t) =\frac{V_{m}}{Z}\sin\left(\omega t-\theta\right)+\frac{V_{m}}{Z}\sin\left(\theta\right)e^{-t/\tau} \\ =\frac{V_{m}}{Z}\Big[\sin\left(\omega t-\theta\right)+\sin\left(\theta\right)e^{-t/\tau}\Big] \end{gathered}\]
  Substituting

• \[i(\omega t)=\frac{V_m}{Z}\Big[\sin{(\omega t-\theta)}+\sin{(\theta)}e^{-\omega t/\omega\tau}\Big]\]
  , thus rather than time It is often convenient to write the function in terms of the angle
• \[\begin{aligned} i(\beta) & =\frac{V_m}{Z}\Big[\sin{(\beta-\theta)}+\sin{(\theta)}e^{-\beta/\omega\tau}\Big]=0 \end{aligned}\]
  \[\boxed{\sin(\beta-\theta)+\sin(\theta)e^{-\beta/\omega\tau}=0}\]
  , can be found by , where the The extinction angle

• There is no closed-form solution for \(\beta\), and some numerical method is required

• \[\boxed{i(\omega t)=\begin{cases}\dfrac{V_m}{Z}\Big[\sin{(\omega t-\theta)}+\sin{(\theta)}e^{-\omega t/\omega\tau}\Big]&\quad\mathrm{for}\:0\leq\omega t\leq\beta\\\\0&\quad\mathrm{for}\:\beta\leq\omega t\leq2\pi\end{cases}}\]
  \(\tan ^{- 1}\left ( \dfrac {\omega L}R\right ) ~\text{and}~\tau = \dfrac LR\)\(Z= \sqrt {R^{2}+ ( \omega L) ^{2}} \quad \theta =\)Summary:
• \[I_{\mathrm{rms}}=\sqrt{\frac{1}{2\pi}\int\limits_{0}^{2\pi}i^{2}(\omega t)d(\omega t)}=\sqrt{\frac{1}{2\pi}\int\limits_{0}^{\beta}i^{2}(\omega t)d(\omega t)}\]
  RMS current:
• \[I_o=\frac{1}{2\pi}\int\limits_0^{\beta}i(\omega t)d(\omega t)\]
  Average current: