Single-Phase Diode Rectifier with L-Load
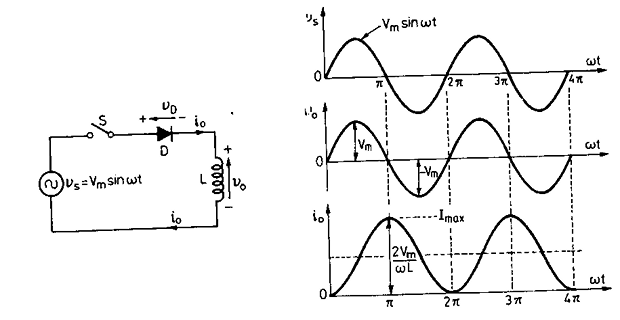
When switch \(S\) closed at \(\omega t = 0\), the diode starts conducting
- \[\begin{gathered} v_{s}=v_{0}=L\frac{di_{o}}{dt}=V_{m}\sin\omega t \\ i_{0}=\frac{V_{m}}{L}\int\sin\omega t\cdot dt \\ =-\frac{V_{m}}{\omega L}\cos\omega t+A \\ \text{At}~\omega t = 0, \quad i_0 = 0 \Rightarrow 0=-\dfrac{V_m}{\omega L}+A\\ \Rightarrow~A=\dfrac{V_m}{\omega L}\\ \end{gathered}\]Applying KVL in the circuit:
- \[i_{0}=\frac{V_{m}}{\omega L}\left(1-\cos\omega t\right)\]gives: Substituting the value of
- \[v_{0}=L\frac{di_{o}}{dt}=L\frac{V_{m}}{\omega L}[\sin\omega t]\omega=V_{m}\sin\omega t=v_{s}\]Output voltage:
Average value of the output voltage \(v_0=0\)
The output current \(i_0\) consists of dc component and fundamental frequency component of frequency \(\omega\)
- \[I_{\max } =\frac{V_m}{\omega L}(1+1)=\frac{2 V_m}{\omega L}\]occurs at Peak value of current
- \[\begin{aligned} I_0 & =\frac{1}{2 \pi} \int_0^{2 \pi} \frac{V_m}{\omega L}(1 - \cos \omega t) d(\omega t) \\ & =\frac{V_m}{\omega L}=\frac{1}{2} I_{\max } \end{aligned}\]Average value of the current:
Rms value of fundamental current, \(I_{1 r}\) is given by
\[\begin{aligned} I_{1 r} & =\left[\frac{1}{2 \pi}\left(\frac{V_m}{\omega L}\right)^2 \int_0^{2 \pi}(\cos \omega t)^2 d(\omega t)\right]^{1 / 2} \\ & =\frac{V_m}{\sqrt{2} \cdot \omega L}=\frac{V_s}{\omega L}=\frac{I_0}{\sqrt{2}} \\ \end{aligned}\]- \[\begin{aligned} & =\left[I_0^2+I_{1 r}^2\right]^{1 / 2} \\ & =\left[I_0^2+\frac{I_0^2}{2}\right]^{1 / 2}=1.225 I_0 \end{aligned}\]RMS value of the rectified current:
Voltage cross diode \(v_D =0\)
Single-Phase Diode Rectifier with C-Load
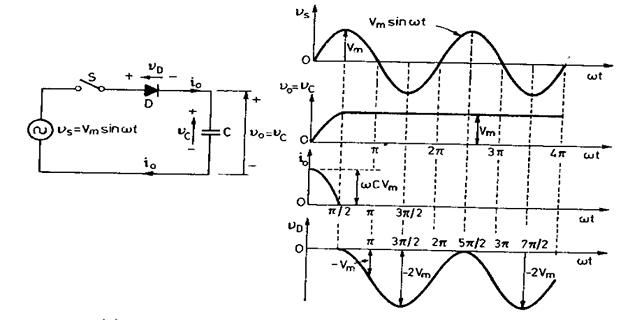
- \[i_{0}=C\frac{dv_{s}}{dt}=C\frac{d}{dt}(V_{s}\sin\omega t) = \omega C V_m \cos \omega t\], then When switch is closed at
- \[v_{0}=\frac{1}{C}\int idt=V_{m}\sin\omega t=v_{s}=v_{C}\]Output voltage:
Capacitor is charged to voltage \(V_m\) at \(\omega t = \dfrac{\pi}{2}\) and subsequently this voltage remains constant at \(V_m\)
Capacitor current or load current is maximum at \(\omega t = 0\) and its value is \(\omega C V_m\)
The diode conducts for \(\dfrac{\pi}{2\omega}\) from \(\omega t = 0\) to \(\omega t = \dfrac{\pi}{2}\) and in this interval diode voltage is zero
- \[\begin{aligned} v_{D}=-v_{0}+v_{s}&=-V_{m}+V_{m}\sin\omega t\\&=V(\sin\omega t-1) ~ \Leftarrow \text{time origin redefined at }~\omega t = \pi/2 \end{aligned}\]is given by: , the diode voltage After
After \(\omega t = \pi/2\) the diode voltage is obtained and at \(\omega t = 3\pi/2,~v_D = -2V_m\)
- \[\begin{aligned} V_D & =\frac{1}{2 \pi} \int_0^{2 \pi} V_m(\sin \omega t-1) d(\omega t) \\ & =V_m=\sqrt{2} V_s \end{aligned}\]Average value of voltage across diode,
- \[V_{1 r}=\left[\frac{1}{2 \pi} \int_0^{2 \pi} V_m^2 \sin ^2 \omega t d(\omega t)\right]^{1 / 2}=\frac{V_m}{\sqrt{2}}\]Rms value of fundamental component of voltage across diode,
- \[=\sqrt{V_D^2+V_{1 r}^2}=1.225 V_m\]Rms value of voltage across diode