Single-Phase Half-Controlled Rectifiers with Resistive and Resistive-Inductive Loads (RE & RLE)

Analysis and Performance Characteristics

Firing Angle Analysis for Transient Current

Firing Angle to Ensure No Transient Current

Key Formula

The firing angle to ensure no transient current is:

\[\boxed{\alpha = \tan^{-1}\left(\frac{\omega L}{R}\right)}\]

  • Where:

    • \(\omega = 2\pi f\) is the angular frequency (rad/s)

    • \(L\) is the inductance (H)

    • \(R\) is the resistance (\(\Omega\))

  • This angle corresponds to the load impedance angle

  • At this firing angle, the transient component becomes zero

Maximum Transient Current Condition

Maximum Transient Condition

For maximum transient current:

\[\begin{aligned} \sin(\alpha - \phi) &= 1 = \sin 90^\circ\\ \therefore \quad \alpha &= 90^\circ + \phi \end{aligned}\]

  • Where \(\phi = \tan^{-1}\left(\frac{\omega L}{R}\right)\) is the load impedance angle

  • This represents the worst-case scenario for transient current

  • Practical implication: Avoid firing at this angle for smooth operation

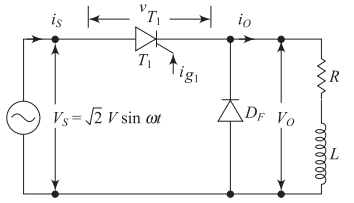
Half-Controlled Converters with RL Load and Freewheeling Diode

Circuit Configuration

  • Components:

    • Single-phase AC source

    • Thyristor (\(T_1\))

    • RL load (R, L)

    • Freewheeling diode (\(D_f\))

  • Purpose of freewheeling diode:

    • Provides path for inductive current

    • Improves converter performance

    • Reduces voltage stress on thyristor

Single-phase half-controlled converter with RL load and freewheeling diode
Single-phase half-controlled converter with RL load and freewheeling diode

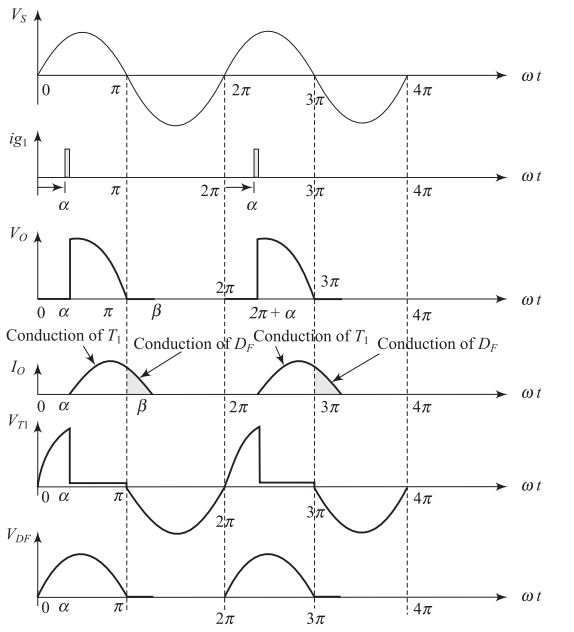
Discontinuous Mode Operation

Discontinuous Mode: Operating Principle

Mode I: Thyristor Conduction (\(\alpha < \omega t < \pi\))

  • Thyristor \(T_1\) is forward biased during positive half-cycle

  • Triggering pulse applied at \(\omega t = \alpha\)

  • Current flows: Source \(\rightarrow\) \(T_1\) \(\rightarrow\) Load

Mode II: Freewheeling Diode Conduction (\(\pi < \omega t < \pi + \beta\))

  • Input polarity reverses at \(\omega t = \pi\)

  • Inductive current continues through \(D_f\)

  • Current flows: \(D_f\) \(\rightarrow\) Load (decaying)

  • Current becomes zero at \(\omega t = \pi + \beta\)

Waveforms of a single-phase half-controlled converter with RL load and freewheeling diode (Discontinuous Mode)
Waveforms of a single-phase half-controlled converter with RL load and freewheeling diode (Discontinuous Mode)

Discontinuous Mode: Performance Analysis

Average Output Voltage

\[\boxed{V_o = V_{dc} = \frac{V_m}{2\pi} (1 + \cos \alpha)}\]

Average Output Current

\[\boxed{I_o = I_{dc} = \frac{V_m}{2\pi R} (1 + \cos \alpha)}\]

  • Note: \(V_m = \sqrt{2}V\) is the peak input voltage

  • Output voltage is higher compared to without freewheeling diode

  • Current ripple is reduced due to freewheeling action

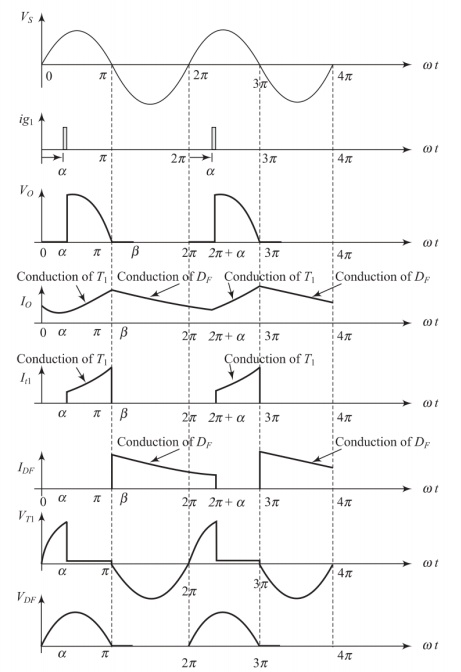
Continuous Mode Operation

Continuous Mode: Mode I Analysis

Mode I: Thyristor \(T_1\) Conduction (\(\alpha < \omega t < \pi\))

Voltage equation:

\[\sqrt{2} V \sin \omega t = L \frac{di_o}{dt} + Ri_o\]

Output current solution:

\[\boxed{i_o(t) = \frac{\sqrt{2} V}{Z} \sin(\omega t - \phi) + \left[I_o - \frac{\sqrt{2} V}{Z} \sin(\alpha - \phi)\right] e^{-\frac{R}{L}(\omega t - \alpha)}}\]

  • Where: \(Z = \sqrt{R^2 + (\omega L)^2}\) and \(\phi = \tan^{-1}\left(\frac{\omega L}{R}\right)\)

  • \(I_o\) is the initial current at \(\omega t = \alpha\)

Continuous Mode: Mode II Analysis

Mode II: Freewheeling Diode \(D_f\) Conduction (\(\pi < \omega t < 2\pi + \alpha\))

Voltage equation:

\[0 = L \frac{di_o}{dt} + Ri_o\]

Output current solution:

\[\boxed{i_o(t) = I_\pi e^{-\frac{R}{L}(\omega t - \pi)}}\]

  • \(I_\pi\) is the current at \(\omega t = \pi\) (end of Mode I)

  • Current decays exponentially with time constant \(\tau = \frac{L}{R}\)

  • Mode II continues until the next firing pulse at \(\omega t = 2\pi + \alpha\)

Waveforms of a single-phase half-controlled converter with RL load and freewheeling diode (Continuous Mode)
Waveforms of a single-phase half-controlled converter with RL load and freewheeling diode (Continuous Mode)

Advantages of Freewheeling Diode

Performance Improvements

  1. Higher output voltage: Better voltage utilization

  2. Improved power factor: Reduced reactive power demand

  3. Better current waveform: Reduced current ripple

  4. Enhanced efficiency: Energy stored in inductance is transferred to load resistance

  5. Reduced voltage stress: Lower reverse voltage across thyristor

Key Benefit

The stored magnetic energy in inductance \(L\) is efficiently transferred to the resistive load \(R\) during freewheeling, improving overall converter efficiency.

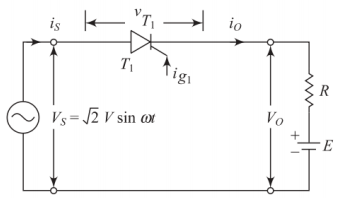
Half-Wave Controlled Converters with RE Load

RE Load Configuration

  • Applications:

    • Battery charging systems

    • DC motor drives

    • Electroplating processes

  • Load components:

    • Resistance (R): Internal resistance

    • EMF source (E): Battery voltage

  • Operation principle:

    • Thyristor conducts when \(V_s > E\)

    • Current flows only during charging

Single-phase half-wave controlled rectifier with RE load
Single-phase half-wave controlled rectifier with RE load

RE Load: Operating Conditions

Conduction Conditions

Thyristor conducts when:

  • Input voltage \(V_s > E\) (forward bias condition)

  • Gate pulse is applied at \(\omega t = \alpha\)

Natural conduction angle:

\[\boxed{\beta_1 = \sin^{-1}\left(\frac{E}{\sqrt{2} V}\right)}\]

  • When \(V_s < E\): Thyristor is reverse biased and turns OFF

  • Extinction angle \(\beta_2 = \pi - \beta_1\) (due to symmetry)

  • Condition for conduction: \(\alpha \leq \beta_1\) for natural conduction

RE Load: Current and Power Analysis

Charging Current

During conduction period \(\beta_1 < \omega t < \beta_2\):

\[\boxed{i_o = \frac{\sqrt{2} V \sin \omega t - E}{R}}\]

Average Charging Current

\[\boxed{I_{dc} = \frac{1}{2\pi R} \int_{\beta_1}^{\beta_2} (\sqrt{2} V \sin \omega t - E) \, d(\omega t)}\]

  • Power delivered to battery: \(P_b = E I_{dc}\)

  • Power loss in resistance: \(P_R = I_{rms}^2 R\)

  • Rectifier efficiency: \(\eta = \frac{P_b}{P_b + P_R}\)

RE Load: Controlled Operation (\(\alpha > \beta_1\))

Modified Operating Range

When firing angle \(\alpha > \beta_1\):

  • Conduction period: \(\alpha < \omega t < \beta_2\)

  • Reduced charging time

  • Lower average charging current

Performance equations

Average charging current:

\[I_{dc} = \frac{1}{2\pi R} \int_{\alpha}^{\beta_2} (\sqrt{2} V \sin \omega t - E) \, d(\omega t)\]

RMS current:

\[I_{rms} = \sqrt{\frac{1}{2\pi R^2} \int_{\alpha}^{\beta_2} (\sqrt{2} V \sin \omega t - E)^2 \, d(\omega t)}\]

Half-Wave Controlled Converters with RLE Load

RLE Load: Introduction and Applications

Load Components

  • R: Armature resistance / Internal resistance

  • L: Armature inductance / Circuit inductance

  • E: Back EMF / Counter EMF

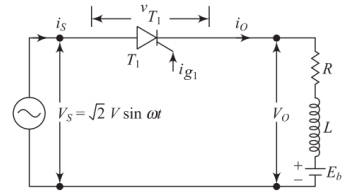
Single-phase half-wave controlled rectifier with RLE load
Single-phase half-wave controlled rectifier with RLE load

Primary Applications

  • DC Motor Control: Armature circuit modeling

  • Battery Charging: With series inductance

  • Electrochemical Processes: Industrial applications

Key Characteristic

RLE load makes the most comprehensive load model for practical applications.

RLE Load: Operating Constraints

Minimum Firing Angle

\[\boxed{\delta_0 = \sin^{-1}\left(\frac{E}{\sqrt{2}V}\right)}\]

  • Constraint: \(\alpha \geq \delta_0\) for thyristor conduction

  • When \(\alpha < \delta_0\): Input voltage \(< E\), thyristor remains OFF

Operating Range

  • Minimum firing angle: \(\alpha_{min} = \delta_0\)

  • Maximum firing angle: \(\alpha_{max} = \pi - \delta_0\)

  • Practical range: \(\delta_0 \leq \alpha \leq \pi - \delta_0\)

RLE Load: Circuit equation and Solution

Voltage equation

When thyristor conducts (\(\alpha < \omega t < \beta\)):

\[\boxed{\sqrt{2}V \sin \omega t = L\frac{di}{dt} + Ri + E}\]

Complete Current Solution

\[\boxed{i(t) = \frac{\sqrt{2}V}{Z}\left[\sin(\omega t - \phi) - \sin(\alpha - \phi)e^{-\frac{R}{L}(t-\frac{\alpha}{\omega})}\right] - \frac{E}{R}\left[1 - e^{-\frac{R}{L}(t-\frac{\alpha}{\omega})}\right]}\]

  • Where: \(Z = \sqrt{R^2 + (\omega L)^2}\) and \(\tan\phi = \frac{\omega L}{R}\)

  • Current has both steady-state and transient components

RLE Load: Performance Parameters

Average Charging Current

\[\boxed{I_{av} = \frac{\sqrt{2}V}{2\pi R}(\cos\alpha - \cos\beta) - \frac{E}{2\pi R}(\beta - \alpha)}\]

Average Output Voltage

\[\boxed{V_{av} = \frac{\sqrt{2}V}{2\pi}(\cos\alpha - \cos\beta) - \frac{E}{2\pi}(\beta - \alpha) + E}\]

  • \(\beta\) is the extinction angle (when current becomes zero)

  • Both voltage and current depend on the conduction angle \((\beta - \alpha)\)

  • Control strategy: Vary \(\alpha\) to control average values

Summary and Key Takeaways

Summary: Key Concepts

Firing Angle Considerations

  • No transient: \(\alpha = \tan^{-1}\left(\frac{\omega L}{R}\right)\)

  • Maximum transient: \(\alpha = 90° + \phi\)

Load Type Characteristics

  • RL Load + Freewheeling Diode: Improved performance, continuous current

  • RE Load: Battery charging, natural conduction constraints

  • RLE Load: DC motor control, combined effects of R, L, and E

Performance Enhancement

  • Freewheeling diode significantly improves converter performance

  • Proper firing angle selection minimizes transients

  • Load characteristics determine operating constraints