Single-Phase Half-Controlled Rectifiers with Resistive and Inductive Loads

Analysis and Performance Characteristics

Introduction to Controlled Rectifiers

Introduction to Controlled Rectifiers

Limitations of Uncontrolled Converters

  • Average output voltage is constant for given load and fixed input voltage

  • Variable output requires additional components:

    • Auto-transformer

    • VARIAC

    • Tap changing transformer

Disadvantages of Traditional Methods

  • Large size and heavy weight

  • High cost and complexity

  • Limited control range

Solution: Phase Controlled Converters

Provide better solutions with compact design and precise control

Applications of Controlled Rectifiers

Industrial Applications

Extensively used in various industrial sectors:

  • Electric traction systems

  • Steel rolling mills

  • Paper mills

  • Textile mills

  • Magnet power supply

  • Electro-mechanical devices

Power Semiconductor Devices

Power Diode Operation

  • ON: Forward biased and input voltage \(>\) cut-off voltage

  • OFF: When reverse biased

SCR Operation

  • ON: Forward biased + triggering pulse applied

  • OFF: Reverse bias or commutation voltage

Key Characteristic

Devices are turned ON and OFF sequentially and repetitively to control power flow

Commutation Methods for SCRs

Natural Commutation

(Line Commutation)

  • SCR turns OFF when applied AC voltage becomes zero

  • Commonly used in controlled rectifier circuits

  • Simple and reliable

Forced Commutation

(Artificial Commutation)

  • Uses specially designed circuit

  • Applies reverse voltage across SCR

  • Forces SCR to turn OFF

Classification of Single-Phase Controlled Rectifiers

Classification Overview

Basic Principle

When diodes are replaced by SCRs in uncontrolled converters:

  • Controllable output voltage obtained by controlling delay angle (\(\alpha\))

  • Variable voltage available at output terminals

Classification Based on Pulses

  • Single-phase half-wave (1-pulse) controlled converter

  • Single-phase full-wave (2-pulse) controlled converter

Detailed Classification

Single-Phase Controlled Converters

  • Half-wave or 1-pulse converters:

    • Without free wheeling diode

    • With free wheeling diode (\(D_F\))

  • Full-wave or 2-pulse converters:

    • Without free wheeling diode (\(D_F\)) - full-converter

    • With free wheeling diode (\(D_F\)) - semi-converter

Half-Controlled Converters with Resistive Load

Circuit Configuration - R Load

Circuit Components

  • Single-phase AC source

  • Thyristor \(T_1\) (controlled switch)

  • Resistive load (R)

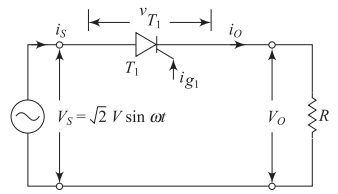
Single-phase half controlled converter with R load
Single-phase half controlled converter with R load

Thyristor Conduction Conditions

Thyristor \(T_1\) conducts only when:

  1. Anode is positive with respect to cathode

  2. Positive gate pulse is applied

Otherwise operates in forward blocking state

Operating Principle - R Load

Positive Half Cycle

  • Thyristor \(T_1\) is forward biased

  • Fired at \(\omega t = \alpha\)

  • Starts conduction

  • Continues up to \(\omega t = \pi\)

Negative Half Cycle

  • Thyristor \(T_1\) is reverse biased

  • Turns OFF at \(\omega t = \pi\)

  • Natural commutation occurs

  • Load current becomes zero

Control Mechanism

Average output voltage is controlled by varying firing angle \(\alpha\)

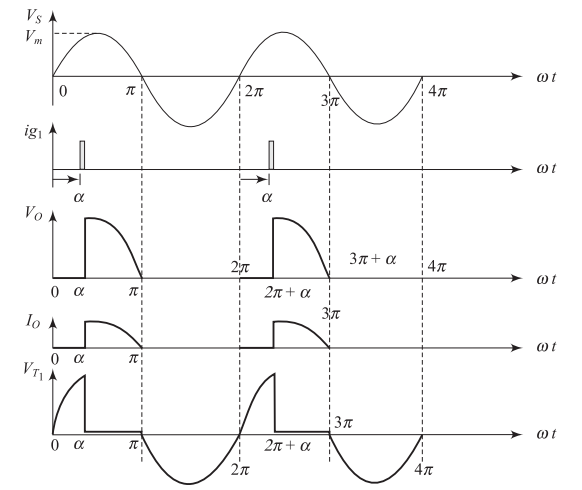
Voltage and current waveforms for Single-phase half controlled converter with R load
Voltage and current waveforms for Single-phase half controlled converter with R load

Key Characteristics - R Load

Waveform Properties

  • Output voltage waveform same as output current waveform

  • Zero phase difference in resistive load

  • DC output voltage always positive

  • Current also positive

Operation Quadrant

  • Operates in first quadrant only

  • Known as half-wave semi-converter

Mathematical Analysis - R Load

Output Voltage Expression

\[\begin{aligned} V_o &= \sqrt{2}V \sin \omega t \quad \text{for } \alpha < \omega t < \pi \\ V_o &= 0 \quad \text{for } 0 < \omega t < \alpha \text{ and } \pi < \omega t < 2\pi \end{aligned}\]

Average Output Voltage

\[\displaystyle V_{dc} = \frac{\sqrt{2}V}{\pi}(1 + \cos \alpha)\]

  • When \(\alpha = 0\): \(V_{dc} = \frac{2\sqrt{2}V}{\pi}\) (Maximum)

  • When \(\alpha = \pi\): \(V_{dc} = 0\) (Minimum)

Performance Parameters - R Load

Voltage and Current Parameters

RMS Output Voltage:

\[\displaystyle V_{rms} = V \sqrt{\frac{1}{2\pi} \left[ (\pi - \alpha) + \frac{\sin 2\alpha}{2} \right]}\]

Average and RMS Current:

\[\begin{aligned} I_{dc} &= \frac{V_{dc}}{R} = \frac{\sqrt{2}V}{\pi R}(1 + \cos \alpha) \\ I_{rms} &= \frac{V_{rms}}{R} \end{aligned}\]

Power Analysis - R Load

Power Calculations

DC Output Power:

\[\displaystyle P_{dc} = V_{dc} \times I_{dc} = \frac{2V^2}{\pi^2 R}(1 + \cos \alpha)^2\]

AC Output Power:

\[P_{ac} = V_{rms} \times I_{rms} = \frac{V^2}{2\pi R} \left[ (\pi - \alpha) + \frac{\sin 2\alpha}{2} \right]\]

Quality Factors - R Load

Form Factor

\[\displaystyle FF = \frac{I_{rms}}{I_{dc}} = \frac{\pi \sqrt{\frac{1}{2\pi} \left[ (\pi - \alpha) + \frac{\sin 2\alpha}{2} \right]}}{1 + \cos \alpha}\]

Ripple Factor

\[RF = \sqrt{FF^2 - 1}\]

Transformer Utilization Factor (TUF)

\[TUF = \frac{P_{dc}}{VA} = \frac{2(1 + \cos \alpha)^2}{\pi^2 \sqrt{\frac{1}{2\pi} \left[ (\pi - \alpha) + \frac{\sin 2\alpha}{2} \right]}}\]

Firing Angle Analysis - R Load

Key Operating Points

Maximum Average Output (50% condition):

  • Maximum average output voltage at \(\alpha = 0°\)

  • For 50% of maximum: \((1 + \cos\alpha) = 1\)

  • Result: \(\alpha = 90°\)

Control Range

DC output voltage varies from \(\frac{2\sqrt{2}V}{\pi}\) to \(0\) when firing angle varies from \(\alpha = 0\) to \(\alpha = \pi\)

Half-Controlled Converters with RL Load

Circuit Configuration - RL Load

Circuit Components

  • AC voltage source

  • Thyristor (controlled switch)

  • Resistive-inductive load (RL)

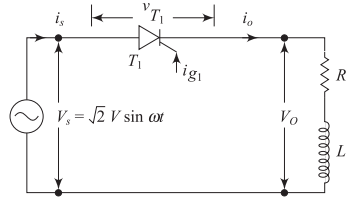
Single-phase half controlled converter with RL load
Single-phase half controlled converter with RL load

Key Difference

Operation differs significantly from pure resistive load due to inductance effects

Operating Principles - RL Load

Positive Half-Cycle Operation

  • Thyristor forward biased

  • Gate pulse applied at \(\omega t = \alpha\)

  • Thyristor turns ON

  • Input voltage applied across load

Inductive Load Effects

  • Current increases gradually from zero

  • Reaches maximum, then decreases

  • Current continues to flow even after input voltage reverses

Conduction Characteristics - RL Load

Conduction Period Definition

  • Thyristor starts conduction: \(\omega t = \alpha\) (firing angle)

  • Thyristor turns OFF: \(\omega t = \beta\) (extinction angle)

  • Conduction period: \(\beta - \alpha\) (conduction angle)

Important Note

Thyristor remains ON despite reverse bias due to inductive current continuation

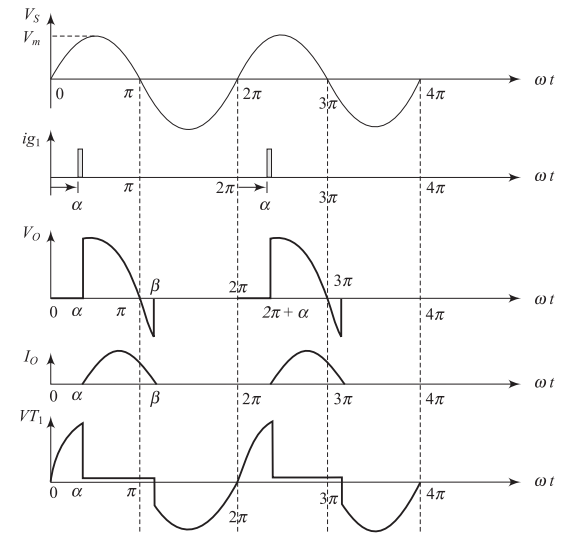
Voltage and current waveforms for Single-phase half controlled converter with RL load
Voltage and current waveforms for Single-phase half controlled converter with RL load

Output Voltage Expression - RL Load

Piecewise Voltage Expression

\[\begin{aligned} v_o &= V_m \sin \omega t \quad \text{for} \quad \alpha < \omega t < \beta \\ v_o &= 0 \quad \text{for} \quad 0 < \omega t < \alpha \text{ and } \beta < \omega t < 2\pi \end{aligned}\]

Two Operating Modes

  • Rectification mode (\(\alpha < \omega t < \pi\)): Power flows from supply to load

  • Inversion mode (\(\pi < \omega t < \beta\)): Power flows from load to supply

Current Analysis - RL Load

Circuit Voltage Equation

When thyristor is ON:

\[V_m \sin \omega t = L\frac{di_o}{dt} + Ri_o\]

Current Components

Steady-state: \(i_{ss}(t) = \frac{V_m}{Z} \sin(\omega t - \phi)\)
Transient: \(i_{tr}(t) = Ae^{-\frac{R}{L}t}\)

Where: \(Z = \sqrt{R^2 + (\omega L)^2}\) and \(\tan \phi = \frac{\omega L}{R}\)

Complete Current Expression - RL Load

Total Output Current

\[\displaystyle i_o(t) = \frac{V_m}{Z} \left[ \sin(\omega t - \phi) - \sin(\alpha - \phi)e^{-\frac{R}{L}(t-\frac{\alpha}{\omega})} \right]\]

Boundary Condition

At extinction angle: \(i_o = 0\) when \(\omega t = \beta\)

\[\sin(\beta - \phi) = \sin(\alpha - \phi)e^{-\frac{R}{\omega L}(\beta - \alpha)}\]
This equation determines the extinction angle \(\beta\)

Voltage Analysis - RL Load

Average Output Voltage

\[\displaystyle V_{av} = \frac{V_m}{2\pi} (\cos \alpha - \cos \beta)\]

  • Maximum when \(\beta = \pi\)

  • Decreases as \(\beta\) increases

RMS Output Voltage

\[V_{rms} = \frac{V_m}{\sqrt{2}} \sqrt{\frac{1}{2\pi} \left[ (\beta - \alpha) - \frac{1}{2}(\sin 2\beta - \sin 2\alpha) \right]}\]

Form Factor Analysis - RL Load

Form Factor Definition

\[\text{Form Factor} = \frac{V_{rms}}{V_{av}}\]

Simplified Expression

\[\displaystyle FF = \frac{\sqrt{\pi} \sqrt{(\beta - \alpha) - \frac{1}{2}(\sin 2\beta - \sin 2\alpha)}}{\cos \alpha - \cos \beta}\]

Form factor indicates the shape of the output waveform

Transient Analysis - RL Load

Transient Current Component

\[i_{tr}(t) = -\frac{V_m}{Z} \sin(\alpha - \phi)e^{-\frac{R}{L}(t-\frac{\alpha}{\omega})}\]

Special Cases

  • No transient current: when \(\sin(\alpha - \phi) = 0\)

  • Maximum transient: when \(\sin(\alpha - \phi) = \pm 1\)

These conditions are important for circuit design and protection

Quadrant Operation - RL Load

Two-Quadrant Operation

Single-phase half-wave controlled rectifier with RL load operates in:

  • First quadrant: Rectification mode

  • Fourth quadrant: Inversion mode

Key Features

  • Average output voltage can be positive or negative

  • Depends on firing angle

  • Bidirectional power flow capability

  • Makes it a "full converter"

Summary and Applications

Summary

Single-Phase Half-Wave Controlled Rectifiers

With R Load:

  • Simpler analysis

  • Current follows voltage

  • First quadrant operation

With RL Load:

  • Complex due to inductance

  • Two-quadrant operation

  • Bidirectional power flow

Key Control Parameters

  • Firing angle \(\alpha\) controls output

  • Extinction angle \(\beta\) depends on load characteristics

  • Conduction angle \(\beta - \alpha\) determines power transfer

Applications

Practical Applications

Power Supplies

  • DC power supplies

  • Variable voltage sources

Energy Storage

  • Battery charging

  • Energy recovery systems

Motor Control

  • DC motor control

  • Speed regulation

Advantages

  • Precise voltage control

  • High efficiency

  • Compact design

  • Cost-effective solution