Power Diodes & Complex Loads: Demystifying the Switched RLC Circuit

Diode Switched RLC Load:

\[\begin{aligned} & L\frac{di}{dt}+Ri+\frac{1}{C}\int idt+v_c(t=0)=V_s \\ & \frac{d^2i}{dt^2}+\frac{R}{L}\frac{di}{dt}+\frac{i}{LC}=0 \Rightarrow s^2+\frac{R}{L}s+\frac{1}{LC}=0 ~~ \Leftarrow \textbf{characteristic equation}\\ & s_{1,2}=-\dfrac{R}{2L}\pm\sqrt{\left(\dfrac{R}{2L}\right)^2-\dfrac{1}{LC}}\\ &\alpha=\frac{R}{2L} ~~\Leftarrow \textbf{Damping factor} \qquad \omega_0=\frac{1}{\sqrt{LC}}~~\Leftarrow \textbf{Resonant frequency}\\ & s_{1,2}=-\alpha\pm\sqrt{\alpha^2-\omega_0^2}~~ \Leftarrow \textbf{Roots of the characteristic equation}\\ \end{aligned}\]

\[i(t)=\left(A_1+A_2 t\right) e^{s_1 t}\]

, and the circuit is called critically damped. The solution takes the form , the roots are equal, If

\[i(t)=A_1 e^{s_1 t}+A_2 e^{s_2 t}\]

, the roots are real and the circuit is said to be overdamped. The solution takes the form If

\[s_{1,2}=-\alpha \pm j \omega_r\]

\[i(t)=e^{-\alpha t}\left(A_1 \cos \omega_r t+A_2 \sin \omega_r t\right)\]

\(\omega_r=\sqrt{\omega_0^2-\alpha^2}\)\(\omega_r\), the roots are complex and the circuit is said to be underdamped. The roots are If

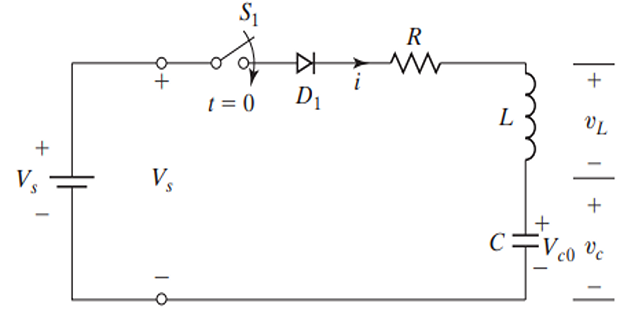
A switched underdamped \(RLC\) circuit is used to convert a dc supply voltage into an ac voltage at the damped resonant frequency.
The constants \(A_1\) and \(A_{2}\) can be determined from the initial conditions of the circuit.
Solving for these two constants requires two boundary equations at \(i(t=0)\) and \(di/dt(t=0)\) .
The ratio of \(\alpha/\omega_0\) is commonly known as the damping ratio, \(\delta=R/2\sqrt{C/L.}\)
Power electronic circuits are generally underdamped such that the circuit current becomes near sinusoidal, to cause a nearly sinusoidal ac output or to turn off a power semiconductor device.
For critical and underdamped conditions, the current \(i(t)\) will not oscillate and there is no need for the diode.
Equations are the general forms for the solution of any second-order differential equations. The particular form of the solution will depend on the values of \(R, L,\) and \(C.\)

Solved Problem:

The second-order \(RLC\) circuit has the dc source voltage \(V_s=220\mathbb{V}\), \(L= 2\)mH, \(C=0.05~\mu F\), and \(R=160\Omega\). The initial value of the capacitor voltage is \(v_c(t=0)=V_{c0}=0\) and inductor current \(i( t= 0) = 0.\) If switch \(S_1\) is closed at \(t=0\), determine:

an expression for the current \(i(t)\)

\[\begin{aligned} \alpha &=R / 2 L=160 \times 10^3 /(2 \times 2)=40,000 \mathrm{rad} / \mathrm{s} \\ \omega_0 & =1 / \sqrt{L C}=10^5 \mathrm{rad} / \mathrm{s}\\ \omega_r & =\sqrt{10^{10}-16 \times 10^8}=91,652 \mathrm{rad} / \mathrm{s} \\ \alpha&<\omega_0 \Leftarrow ~\text{under-damped circuit }\\ i(t) & =e^{-\alpha t}\left(A_1 \cos \omega_r t+A_2 \sin \omega_r t\right) \end{aligned}\]

\[i(t)=e^{-\alpha t} A_2 \sin \omega_r t\]
. The solution becomes and this gives At
\[\begin{aligned} \frac{d i}{d t} & =\omega_r \cos \omega_r t A_2 e^{-\alpha t}-\alpha \sin \omega_r t A_2 e^{-\alpha}\\ \left.\frac{d i}{d t}\right|_{t=0}&=\omega_r A_2=\frac{V_s}{L}\\ A_2 & =\frac{V_s}{\omega_r L}=\frac{220 \times 1,000}{91,652 \times 2}=1.2 \mathrm{~A}\\ i(t) & =1.2 \sin (91,652 t) e^{-40,000 t} \mathrm{~A} \end{aligned}\]
the conduction time of diode.

\[\omega_{\mathrm{r}} t_1=\pi \quad \text { or } \quad t_1=\frac{\pi}{91,652}=34.27 \mu \mathrm{s}\]
. That is, of the diode is obtained when The conduction time

Power diode switched RLC load

Diode Switched RLC Load:

Solved Problem: