Diode Switched RL Load:
\[\begin{aligned}
V_s & = v_L + v_R = L \dfrac{di}{dt}+Ri \\
\text{Solution} ~i(t) & = \dfrac{V_s}{R} (1-e^{-tR/L})
\qquad i(t=0)=0\\
\dfrac{di}{dt} & = \dfrac{V_s}{L}e^{-tR/L}\\
\left.\dfrac{di}{dt}\right|_{t=0} & = \dfrac{V_s}{L}\\
v_L(t) & = L\dfrac{di}{dt} = V_s e^{-tR/L}
\end{aligned}\]
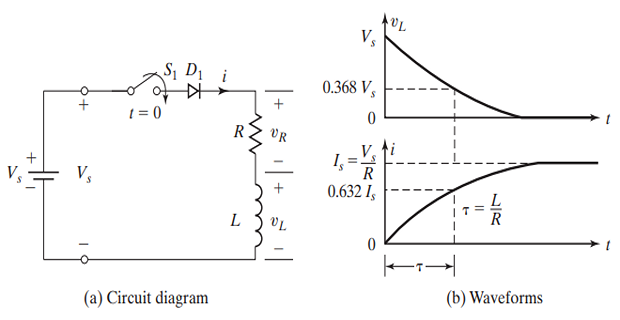
D1 prevents reverse current flow with AC, not DC.
Electronic switches - BJT, MOSFET, IGBT blocks reverse current.
D1 and switch mimic electronic switch behavior.
Energy dissipates as sparks across the switch, risking damage to diode.
To prevent this, a freewheeling diode is connected across an inductive load.
Solved Problem:
A diode \(RL\) circuit with \(V_{S}= 220V, R= 4\Omega,\) and \(L= 5\) mH.The inductor has no initial current. If switch is closed at \(t= 0\), determine
- \[I_P=\frac{V_S}{R}=\frac{220}{4}=55\mathrm{A}\]The steady-state diode current
- \[W=0.5\mathrm{LI}_{\mathrm{P}}^{2}=0.5\times5\times10^{-3} \times 55^{2}=7.563\mathrm{mJ}\]The energy stored in the inductor
- \[\frac{di}{dt}=\frac{V_S}{L}=\frac{220}{5\times10^{-3}}=44\text{A/ms}\]The initial
- \[i(t=1\mathrm{ms})=\frac{V_S}{R}\left(1-e^{-tR/L}\right)=\frac{220}{4}\times\left(1-e^{-1/1.25}\right)=30.287\mathrm{A}\]The inductor current at