Diode Switched RC Load:
An ideal diode with RC Load
- \[t_{rr} = 0 ~\text{and} ~ V_D = 0\]) are negligible ) and forward voltage drop (Ideal means reverse recovery time (
The source voltage (\(V_s\)) is a dc constant voltage
Switch \(S_1\) closed at \(t=0\), the charging current \(i\) flows
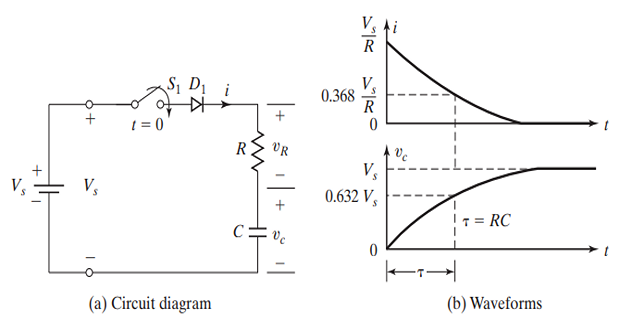
\[\begin{aligned}
& V_s=v_R+v_c=v_R+\frac{1}{C} \int_{t_0}^t i d t+v_c(t=0) \\
& v_R=R i
\end{aligned}\]
\[i(t)=\frac{V_s}{R} e^{-t / R C}\]
as , gives the charging current
With initial condition
- \[v_c(t)=\frac{1}{C} \int_0^t i d t=V_s\left(1-e^{-t / R C}\right)=V_s\left(1-e^{-t / \tau}\right)\]is The capacitor voltage
\(\tau=R C\) is the time constant of an \(R C\) load.
- \[\frac{d v_c}{d t}=\frac{V_s}{R C} e^{-t / R C}\]The rate of change of the capacitor voltage is
- \[\left.\frac{d v_c}{d t}\right|_{t=0}=\frac{V_s}{R C}\]) is The initial rate of change of the capacitor voltage (at
The current \(i\) is unidirectional and does not tend to change its polarity, the diode has no effect on circuit operation.
Problem:
A diode circuit with \(R=44 \Omega\) and \(C=0.1 \mu \mathrm{F}\) load has initial capacitor voltage, \(V_{c 0}=V_c(t=0)=220 \mathrm{~V}\). If switch \(S_1\) is closed at \(t=0\), determine
the peak diode current
the energy dissipated in the resistor \(R\)
the capacitor voltage at \(t=2 \mu \mathrm{s}\).
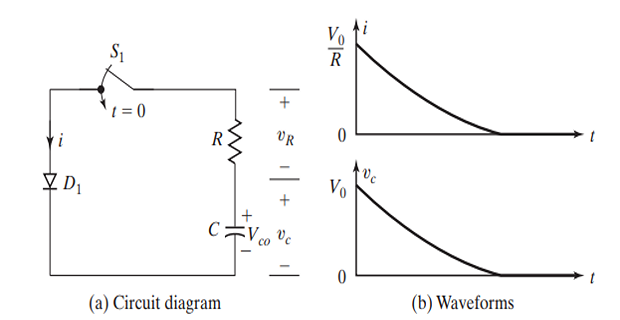
Solution:
- \[I_P=\frac{V_{c 0}}{R}=\frac{220}{44}=5 \mathrm{~A}\]is The peak diode current
- \[W=0.5 C V_{c 0}^2=0.5 \times 0.1 \times 10^{-6} \times 220^2=0.00242 \mathrm{~J}=2.42 \mathrm{~mJ}\]dissipated is The energy
- \[v_c(t=2 \mu \mathrm{s})=V_{c 0} e^{-t / R C}=220 \times e^{-2 / 4.4}=139.64 \mathrm{~V}\], the capacitor voltage is and For