Recovery of Trapped Energy with a Diode:
For ideal lossless circuit \(R=0\), the energy stored in \(L\) remains trapped.
In practical circuits, enhancing efficiency involves returning stored energy back to the power source.
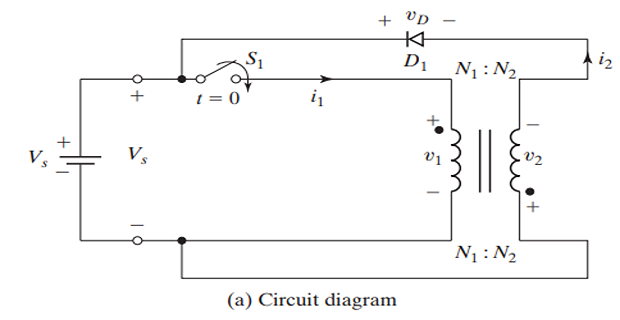
Achieved by adding a second winding to \(L\) and connecting a diode \(D_1\).
Combination of \(L\) and secondary winding functions as a transformer.
The secondary winding is arranged such that when \(v_1\) is positive, \(v_2\) is negative with respect to \(v_1\), and vice versa.
The secondary winding responsible for returning stored energy to the source via \(D_1\) is termed a feedback winding.
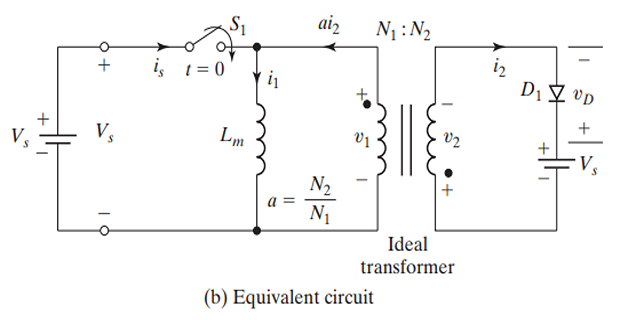
Assuming a transformer with a magnetizing inductance \(L_m\)
Referring the diode and secondary source voltage to the primary side of the transformer:
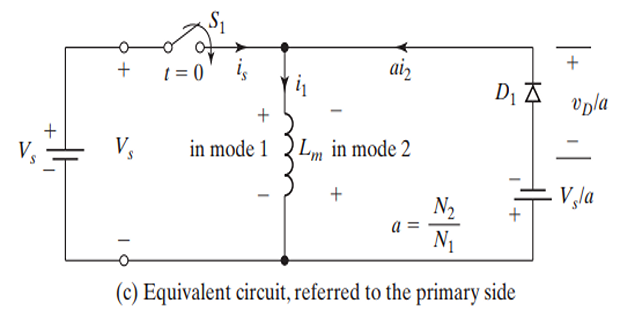\[a = \dfrac{N_2}{N_1} \Leftarrow~\text{Turns ratio }\]
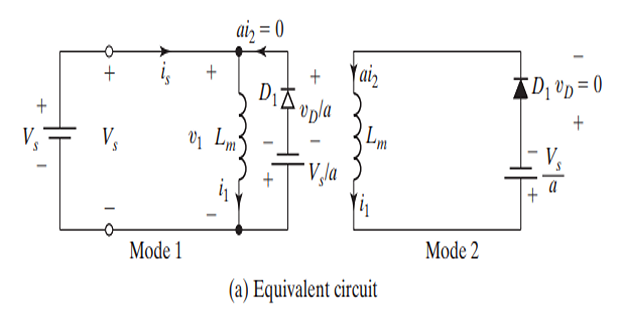
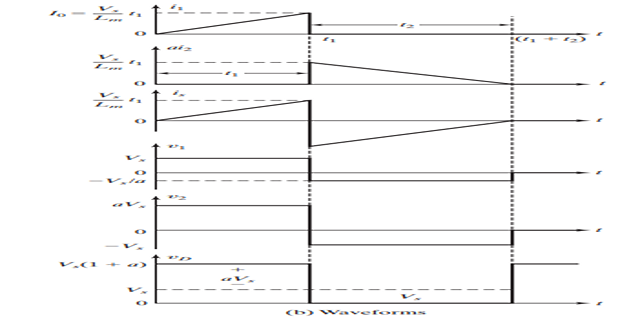
Mode-1:
\(S_1\) closed at \(t=0~\Rightarrow~D_1\) reverse biased \(\Rightarrow~i_2=0\) \[\begin{aligned} V_s & = (v_d-V_s)/a\\ \Rightarrow ~v_d & = V_s(1+a) \\ V_s & = L_m \cdot \dfrac{di_1}{dt} \qquad (i_1=i_s)\\ i_1(t) & =i_s(t) = \dfrac{V_s}{L_m} \cdot t \quad \forall ~0 \leq t \leq t_1\\ \end{aligned}\]
At the end of this mode, the primary current: \[I_0 = \dfrac{V_s}{L_m} \cdot t_1\]
Mode-2:
\(S_1\) opens \(\Rightarrow\) voltage across \(L\) reversed \(\Rightarrow\) \(D_1\) forwards biased \[\begin{aligned} & L_m \cdot \dfrac{di_1}{dt} + \dfrac{V_s}{a} = 0 \\ \text{with}~~ i_1(t=0)=I_0,&~\text{solving} \\ & i_1(t) = -\dfrac{V_s}{aL_m}\cdot t + I_0 \quad \forall~ 0 \leq t \leq t_2\\ \text{Conduction time}~~t_2 & = \dfrac{aL_mI_o}{V_s} = a\cdot t_1 \qquad i_1(t=t_2)=0 \end{aligned}\]
At the end of this mode all the energy stored in \(L_m\) is returned to the source.
Solved Problem:
For the energy recovery circuit, \(V_s = 220~\mathrm{V}\), \(L_m = 250~\mu\mathrm{H}\), \(N_1 = 10\), \(N_2 =100\), and there is no initial circuit current. If switch is closed for time \(t_1=50~\mu\mathrm{s}\) and then opened. Determine the following:
the reverse voltage of the diode, \[\begin{aligned} a & =N_2/N_1=100/10=10\\ v_{D} & =V_{s}(\:1\:+\:a\:)\:=\:220\:\times\:(\:1\:+\:10\:)\:=\:2420\:\mathrm{V} \end{aligned}\]
the peak value of the primary current,
\[I_0=\frac{V_s}{L_m}t_1=220\times\:\frac{50}{250}=44\:\mathrm{A}\]
The peak value of the secondary current \(I_0^{\prime}=I_0/a=44/10=4.4\) A
the conduction time of the diode
\[t_2=\frac{aL_mI_0}{V_s}=250\times44\times\:\frac{10}{220}=500\:\mu s\]
The source energy,
\[W=0.5L_mI_0^2=0.5\times250\times10^{-6}\times44^2=0.242\mathrm{J}=242\mathrm{mJ}\]