Single Phase Uncontrolled (Diode) Rectifier
Demonstrative Video
Introduction to the experiment
This experiment is aimed at converting AC (single phase) to DC using a diode (uncontrolled) rectifier. The circuit is implemented in simulation as well as hardware and the performance is studied.
Learning Outcomes:
Operation and analysis of a single phase rectifier for various loads
Introduction to diode rectifier:
A rectifier is a circuit used to convert AC voltage to DC voltage. There are two types of rectifier circuits: uncontrolled and controlled. An uncontrolled rectifier does not have control on the output voltage. The switch used in this case will be a diode.
There are two types of uncontrolled rectifiers: This section emphasizes the single phase full wave bridge diode rectifier. The rectifier is as depicted in Fig. 1. Fig. 2 represents the Full wave rectifier waveform.
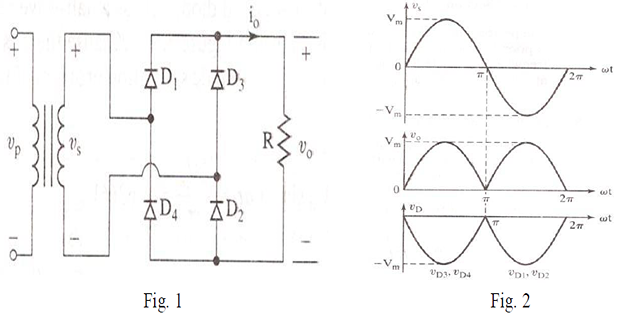
During the positive half cycle of the input supply, the diodes D1 and D2 are conducting, and the output voltage is as depicted in Fig. 2. During the negative half cycle diodes D 3 and D4 conduct. Since the load is resistive, the output voltage follows the input.
1 a). Simulation of full wave DIODE Rectifier in MATLAB Simulink
Aim: To simulate the Diode Rectifier in MATLAB Simulink
PROBLEM 1:
- Implement the 1-phase uncontrolled full wave rectifier with an R load of 25 Ω. (Input voltage: Vpeak=50V=35.35 rms, 50Hz)
- To the above circuit add an L load of 6mH along with the R load of 25 Ω and observe the changes in the output voltage waveform and FFT analysis.
CALCULATION
Form Factor = \(V_{rms}/ V_{dc}\) =
Ripple Factor = \(\sqrt{FF^2-1}\) =
1. b) Hardware Implementation of 1-Phase (R Load )
Procedure for R Load:
- Connect the circuit as shown in Fig. 3 (R=25ohms)
- Switch ON the MCB of 3Ø supply on the Left hand side of your Experimental Table.
- Switch ON the MCB on the POWER MODULE kit.
- Switch ON the MCB on the SCR-Diode Power module and slowly increase the Voltage to reach up to 35.35 V in RMS using + symbol Push Button in the Power Module kit.
- Connect CRO probes across the R load to measure the output voltage.
- Observe the Output voltage waveforms and the FFT plot in the CRO.
Note: The Voltage Adjustment Controls are a pair of push buttons to finely adjust the voltage to required value.
1.c) Hardware Implementation of 1-Phase (RL Load )
Procedure for RL Load:
- Connect the circuit as shown in Fig.4 (R=25ohms, L=6mH))
- Switch ON the MCB of 3Ø supply on the Left hand side of your Experimental Table.
- Switch ON the MCB on the POWER MODULE kit.
- Switch ON the MCB on the SCR-Diode Power module and slowly increase the Voltage to reach up to 35.35 V in RMS using + symbol Push Button in the Power Module kit.
- Connect CRO probes across the RL load to measure the output voltage.
- Observe the Output voltage waveforms and the FFT plot in the CRO.
Note: The Voltage Adjustment Controls are a pair of push buttons to finely adjust the voltage to required value.
RESULTS
I) R-Load
- Attach the waveforms of a) Output Voltage b) Output Current c) Input voltage and d) Input Current in Simulink
- Attach the waveforms of a) Diode Voltage b) Diode current for both positive half cycle (Diode D1) and negative half cycle (Diode D3) in Simulink
- Attach the FFT bar chart along with the corresponding waveforms for Input current in Simulink
- Attach the waveforms of a) Output Voltage b) FFT Plot at fundamental frequency (experimentally from the DSO)
II) RL-Load
- Attach the waveforms of a) Output Voltage b) Output Current c) Input voltage and d) Input Current in Simulink
- Attach the waveforms of a) Diode Voltage b) Diode current for both positive half cycle (Diode D1) and negative half cycle (Diode D3) in Simulink
- Attach the FFT bar chart along with the corresponding waveforms for Input current in Simulink
- Attach the waveforms of a) Output Voltage b) FFT Plot at fundamental frequency (experimentally from the DSO)
- Calculate Performance parameters (Simulink)
|
|
R Load |
RL load |
|
VRMS |
|
|
|
IRMS |
|
|
|
VAVG |
|
|
|
IAVG |
|
|
|
Form factor |
|
|
|
Ripple Factor |
|
|
|
FFT Analysis |
||
|
Output Voltage |
||
|
THD in % |
|
|
|
VFundamental (RMS) |
|
|
|
2nd Harmonics (V) (RMS) |
|
|
|
3rd Harmonics (V) (RMS) |
|
|
|
Input Current |
||
|
THD in % |
|
|
|
IFundamental (RMS) |
|
|
|
2nd Harmonics (I) (RMS) |
|
|
|
3rd Harmonics (I) (RMS) |
|
|
- Calculate Performance parameters (Experimental)
|
|
R Load |
RL load |
|
VRMS |
|
|
|
VAVG |
|
|
|
Form factor |
|
|
|
Ripple Factor |
|
|
|
FFT Analysis |
||
|
Output Voltage |
||
|
THD in % |
|
|
|
VFundamental (RMS) |
|
|
|
2nd Harmonics (V) |
|
|
|
3rd Harmonics (V) |
|
|
$$ \begin{aligned} & \mathrm{THD}=\sqrt{\frac{V_{AC \, RMS}^2-V_{1 \, RMS}^2}{V_{1 \, RMS}^2}} \times 100 \% \\ & V_{AC \, RMS}=\sqrt{V_{RMS}^2-V_{AVG}^2} \\ & 20 \log \left(\mathrm{V}_{\mathrm{Fundamental}}(\mathrm{RMS})\right)= \_ \_ \_ \_ \_ \_ \_ \_ \mathrm{dB} \end{aligned} $$