Single-Variable Classical Optimization

Key Definitions

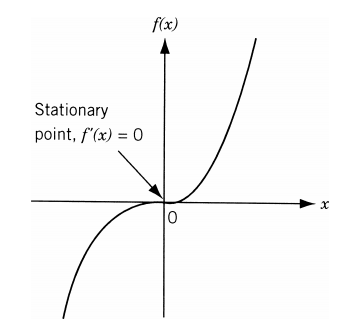
• Stationary point: Where \( f'(x) = 0 \) (necessary condition for an extremum).
• Local minimum: \( f(x^*) \leq f(x) \) in some neighborhood around \( x^* \).
• Global minimum: \( f(x^*) \leq f(x) \) for all \( x \) in the domain.

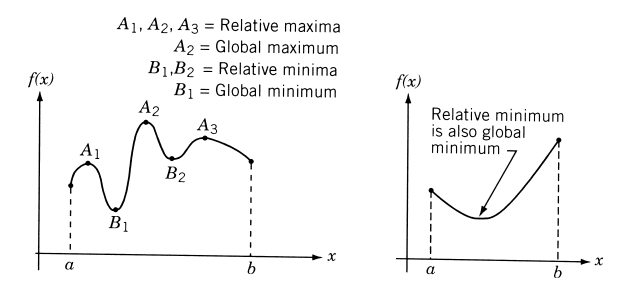
Types of Extrema in Single-Variable Functions

Consider the one-sided derivative at a point \( x^* \):

\[ \lim_{h \to 0} \frac{f(x^* + h) - f(x^*)}{h} = m^+ \text{ (positive) or } m^- \text{ (negative)} \]

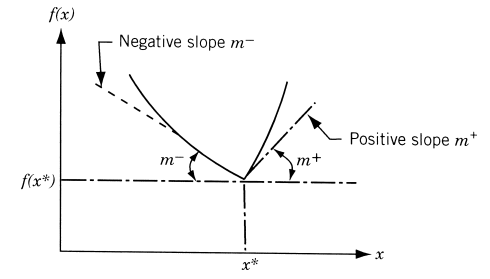
• Derivative undefined at \( x^* \): Possible extremum or cusp.
• Stationary (inflection) point: Where \( f'(x^*) = 0 \) but not an extremum.

First-Order Necessary Condition

If \( f \) is differentiable at \( x^* \) and \( x^* \) is an extremum, then \( f'(x^*) = 0 \).

Second-Order Sufficient Condition

If \( f'(x^*) = 0 \) and:

• \( f''(x^*) > 0 \): Local minimum.
• \( f''(x^*) < 0 \): Local maximum.
• \( f''(x^*) = 0 \): Test fails (use higher-order derivatives).

Important Notes

• Sufficient but not necessary conditions: Extrema may exist without satisfying these.
• Non-differentiable functions: Minima can occur where derivatives don’t exist (e.g., \( f(x) = |x| \)).

Theorem: General Sufficient Condition

Let \( f'(x^*) = f''(x^*) = \cdots = f^{(n-1)}(x^*) = 0 \), but \( f^{(n)}(x^*) \neq 0 \). Then:

• If \( n \) is even and \( f^{(n)}(x^*) > 0 \): Relative minimum.
• If \( n \) is even and \( f^{(n)}(x^*) < 0 \): Relative maximum.
• If \( n \) is odd: Inflection point (no extremum).

Practical Implications

• Second-order test: Sufficient for most engineering problems.
• Higher-order tests: Needed for degenerate cases where lower derivatives vanish.

Example

Find and classify all extrema of \( f(x) = 12x^5 - 45x^4 + 40x^3 + 5 \).

Solution

• First derivative: \( f'(x) = 60x^4 - 180x^3 + 120x^2 = 60x^2(x-1)(x-2) \).
• Critical points: \( x = 0, 1, 2 \) (where \( f'(x) = 0 \)).
• Second derivative: \( f''(x) = 240x^3 - 540x^2 + 240x \).
• Evaluate at critical points:
  • At \( x=1 \): \( f''(1) = 240 - 540 + 240 = -60 < 0 \): Local maximum.
  • At \( x=2 \): \( f''(2) = 1920 - 2160 + 480 = 240 > 0 \): Local minimum.
  • At \( x=0 \): \( f''(0) = 0 \): Test fails.
• Higher derivatives at \( x=0 \): \( f'''(0) = 240 \neq 0 \), \( n=3 \) (odd): Inflection point.