Simplex Method: A Guide to Linear Programming Optimization

Introduction

Introduction to the Simplex Method

  • Developed by George Dantzig in 1947

  • Most widely used method for solving linear programming problems

  • Iterative approach that moves along the edges of the feasible region

  • Based on the fundamental theorem that optimal solution lies at a vertex of the feasible region

Key Insight

Instead of checking all vertices, the simplex method intelligently moves from vertex to vertex, improving the objective function value at each step.

Fundamental Theorem of Linear Programming

If a linear programming problem has an optimal solution, then at least one optimal solution occurs at a vertex (extreme point) of the feasible region.

Implications

  • We only need to check vertices, not the entire feasible region

  • For \(n\) variables and \(m\) constraints, there are at most \(\binom{n}{m}\) vertices

  • Simplex method visits only a small fraction of these vertices

Geometric Interpretation

  • Feasible region is a convex polytope

  • Vertices correspond to basic feasible solutions

  • Edges connect adjacent vertices

  • Simplex method travels along edges

  • Each pivot operation moves to an adjacent vertex

Feasible region showing vertices and simplex path
Feasible region showing vertices and simplex path

Standard Form Requirements

Standard Form

  • Maximization problem

  • All constraints are equations (equalities)

  • All variables non-negative

  • Right-hand side constants are non-negative

Converting to Standard Form

  • Minimization: Multiply objective by -1

  • \(\leq\) constraints: Add slack variables

  • \(\geq\) constraints: Subtract surplus variables, add artificial variables

  • Negative RHS: Multiply constraint by -1

  • Unrestricted variables: Replace with difference of two non-negative variables (\(x = x^+ - x^-\))

  • Equality constraints: Add artificial variables directly

Converting Inequalities - Examples

Original: \(2x_1 + 3x_2 \leq 10\)

Standard: \(2x_1 + 3x_2 + s_1 = 10\), where \(s_1 \geq 0\) (slack variable)

Original: \(x_1 + 2x_2 \geq 5\)

Standard: \(x_1 + 2x_2 - s_2 + a_1 = 5\), where \(s_2, a_1 \geq 0\)

(surplus variable \(s_2\), artificial variable \(a_1\))

Original: \(x_1 + x_2 = 8\)

Standard: \(x_1 + x_2 + a_2 = 8\), where \(a_2 \geq 0\) (artificial variable)

Basic and Non-Basic Variables

Basic Variables

  • One per constraint

  • Form a basis for the solution space

  • Can be positive or zero

  • Number = number of constraints (\(m\))

  • Correspond to identity matrix columns

Non-Basic Variables

  • Set to zero

  • Number = total variables - constraints (\(n-m\))

  • Candidates for entering the basis

  • Correspond to non-identity matrix columns

Matrix Form

\[\begin{aligned} \text{Maximize } & z = c^T x \\ \text{Subject to } & Ax = b \\ & x \geq 0 \end{aligned}\]

Basic Feasible Solution (BFS)

A Basic Feasible Solution is obtained by:

  • Setting \((n-m)\) variables to zero (non-basic)

  • Solving for remaining \(m\) variables (basic)

  • All variables must be non-negative

Properties of BFS

  • Corresponds to a vertex of the feasible region

  • At most \(m\) variables can be positive

  • If unique, it’s a non-degenerate BFS

  • If some basic variables are zero, it’s a degenerate BFS

Example

For \(m = 2\) constraints and \(n = 4\) variables: Set 2 variables to zero, solve for remaining 2 variables

Simplex Algorithm

Simplex Algorithm Steps

Complete Algorithm Overview

  1. Convert LP to standard form

  2. Find initial basic feasible solution (BFS)

  3. Set up initial simplex tableau

  4. Optimality Test: Check if current solution is optimal

  5. If not optimal:

    • Select entering variable (pivot column)

    • Select leaving variable (pivot row) using ratio test

    • Perform pivot operation

    • Update tableau and basis

  6. Repeat steps 4-5 until optimal solution is found or problem is identified as unbounded/infeasible

Finding Initial Basic Feasible Solution

Case 1: All constraints are \(\leq\) type

  • Add slack variables

  • Slack variables form initial basis

  • Example: \(x_1 + 2x_2 \leq 4 \Rightarrow x_1 + 2x_2 + s_1 = 4\)

  • Initial BFS: \(x_1 = 0, x_2 = 0, s_1 = 4\)

Case 2: Mixed constraints

  • Need artificial variables for \(\geq\) and \(=\) constraints

  • Use Big M method or Two-Phase method

  • Artificial variables must be driven out of basis

Big M Method

  • Add artificial variables with large penalty coefficient \(M\) (where \(M \to \infty\))

  • For maximization: subtract \(M \times\) artificial variables from objective

  • For minimization: add \(M \times\) artificial variables to objective

  • Ensures artificial variables are eliminated from optimal solution

Example:

Original: Maximize \(z = 3x_1 + 2x_2\)

Constraint: \(x_1 + x_2 \geq 4\)

Modified: \(x_1 + x_2 - s_1 + a_1 = 4\)

New objective: \(z = 3x_1 + 2x_2 - Ma_1\)

Important

If artificial variables remain in final solution with positive values, the original problem is infeasible.

Two-Phase Method

Phase I

  • Minimize sum of artificial variables

  • Objective: Minimize \(w = \sum a_i\)

  • If minimum value is \(0\), original problem has feasible solution

  • If minimum value \(> 0\), original problem is infeasible

Phase II

  • Remove artificial variables from tableau

  • Use original objective function

  • Continue with regular simplex method

  • Initial BFS for Phase II comes from Phase I optimal solution

Advantages over Big M

  • No need to choose appropriate value of \(M\)

  • Better numerical stability

  • Clearer identification of infeasibility

Pivot Selection Rules

Entering Variable Selection

For Maximization:

  • Choose variable with most negative reduced cost

  • Alternative: Choose first negative reduced cost (Bland’s rule)

For Minimization:

  • Choose variable with most positive reduced cost

Leaving Variable Selection (Ratio Test)

\[\theta = \min\left\{\frac{b_i}{a_{ij}} \mid a_{ij} > 0, i = 1,2,\ldots,m\right\}\]

  • Choose row \(r\) where minimum ratio occurs

  • If tie occurs, choose row with smallest index (Bland’s rule)

  • If no \(a_{ij} > 0\), problem is unbounded

Reduced Costs and Optimality

Reduced cost of variable \(x_j\): \(\bar{c}_j = c_j - c_B^T B^{-1} A_j\)

In tableau form: \(\bar{c}_j = c_j - \sum_{i \text{ basic}} c_i \cdot y_{ij}\)

Optimality Conditions

  • Maximization: Optimal if all \(\bar{c}_j \leq 0\) for non-basic variables

  • Minimization: Optimal if all \(\bar{c}_j \geq 0\) for non-basic variables

  • If \(\bar{c}_j = 0\) for non-basic variable, multiple optimal solutions exist

Economic Interpretation

Reduced cost represents the rate of change in objective function value per unit increase in the variable.

Tableau Method

Setting Up the Simplex Tableau

Basic \(x_1\) \(x_2\) \(s_1\) \(s_2\) RHS Ratio
\(z\) \(-c_1\) \(-c_2\) 0 0 0 -
\(s_1\) \(a_{11}\) \(a_{12}\) 1 0 \(b_1\) \(b_1/a_{1j}\)
\(s_2\) \(a_{21}\) \(a_{22}\) 0 1 \(b_2\) \(b_2/a_{2j}\)

  • First row: objective function coefficients (negated for maximization)

  • Subsequent rows: constraint equations

  • Basic variables have identity matrix columns

  • RHS column shows current solution values

  • Ratio column used for leaving variable selection

Performing Pivot Operations

  1. Select pivot column (entering variable)

  2. Select pivot row using ratio test (leaving variable)

  3. Mark pivot element \(a_{rj}\)

  4. Normalize pivot row: Divide entire pivot row by pivot element

  5. Update other rows: For each row \(i \neq r\):

    \[\text{New row } i = \text{Old row } i - a_{ij} \times \text{New pivot row}\]

  6. Update basis: Replace leaving variable with entering variable

Pivot Operation Goal

Make pivot column look like: \(\begin{bmatrix} 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{bmatrix}\) (1 in pivot row, 0 elsewhere)

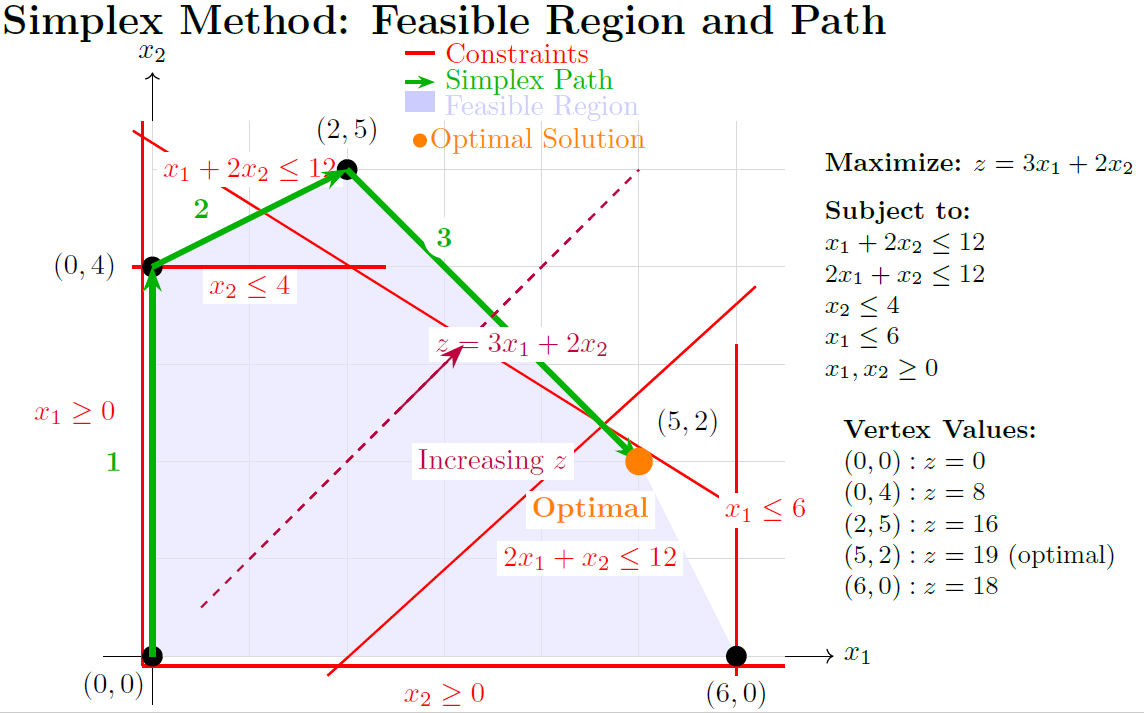
Complete Worked Example - Setup

Example : Product Mix Problem

Maximize \(z = 3x_1 + 5x_2\)

Subject to:

\[\begin{aligned} x_1 &\leq 4 \\ 2x_2 &\leq 12 \\ 3x_1 + 2x_2 &\leq 18 \\ x_1, x_2 &\geq 0 \end{aligned}\]

Standard form:

\[\begin{aligned} x_1 + s_1 &= 4 \\ 2x_2 + s_2 &= 12 \\ 3x_1 + 2x_2 + s_3 &= 18 \end{aligned}\]

Complete Worked Example - Initial Tableau

Basic \(x_1\) \(x_2\) \(s_1\) \(s_2\) \(s_3\) RHS Ratio
\(z\) -3 -5 0 0 0 0 -
\(s_1\) 1 0 1 0 0 4 -
\(s_2\) 0 2 0 1 0 12 6
\(s_3\) 3 2 0 0 1 18 9

  • Initial BFS: \(x_1 = 0, x_2 = 0, s_1 = 4, s_2 = 12, s_3 = 18\)

  • Objective value: \(z = 0\)

  • Most negative coefficient: \(-5\) (column \(x_2\)) \(\to\) Entering variable

  • Ratio test: \(\min\{-, 12/2, 18/2\} = 6\) \(\to\) \(s_2\) leaving

Complete Worked Example - Iteration 1

Basic \(x_1\) \(x_2\) \(s_1\) \(s_2\) \(s_3\) RHS Ratio
\(z\) -3 0 0 2.5 0 30 -
\(s_1\) 1 0 1 0 0 4 4
\(x_2\) 0 1 0 0.5 0 6 -
\(s_3\) 3 0 0 -1 1 6 2

  • Current solution: \(x_1 = 0, x_2 = 6, s_1 = 4, s_3 = 6, z = 30\)

  • Still have negative reduced cost: \(-3\) for \(x_1\) \(\to\) Continue

  • Ratio test: \(\min\{4/1, -/0, 6/3\} = 2\) \(\to\) \(s_3\) leaving

Complete Worked Example - Iteration 2

Basic \(x_1\) \(x_2\) \(s_1\) \(s_2\) \(s_3\) RHS
\(z\) 0 0 0 1.5 1 36
\(s_1\) 0 0 1 1/3 -1/3 2
\(x_2\) 0 1 0 0.5 0 6
\(x_1\) 1 0 0 -1/3 1/3 2

  • All reduced costs \(\geq 0\) \(\to\) Optimal solution found!

  • Optimal solution: \(x_1 = 2, x_2 = 6, s_1 = 2\)

  • Maximum objective value: \(z = 3(2) + 5(6) = 36\)

Special Cases

Unbounded Solution

  • Occurs when entering variable has no positive coefficients in constraint rows

  • Ratio test yields no finite minimum

  • Objective function can be increased indefinitely

If entering variable column has all non-positive entries:

\(x_j\) RHS
-2 5
0 8
-1 3

Problem is unbounded! No ratio test possible.

Detection

When trying to find leaving variable, if all \(a_{ij} \leq 0\) in pivot column, then problem is unbounded.

Infeasible Solution

  • No feasible solution exists

  • Constraints are contradictory

Detection Methods

  • Two-Phase method: Phase I minimum \(> 0\)

  • Big M method: Artificial variables remain in final optimal solution with positive values

  • System of constraints has no solution

Example:

System: \(x_1 + x_2 \leq 2\) , \(x_1 + x_2 \geq 5\), \(x_1, x_2 \geq 0\)

These constraints are contradictory \(\to\) Infeasible

Multiple Optimal Solutions

  • Occurs when a non-basic variable has zero reduced cost at optimality

  • Indicates alternative optimal solutions exist

  • Can pivot on zero reduced cost variable to find alternative optima

Example:

Final tableau shows \(\bar{c}_j = 0\) for non-basic variable \(x_j\):

  • Current solution is optimal

  • Can make \(x_j\) basic to get another optimal solution

  • All convex combinations of these solutions are also optimal

Finding All Optimal Solutions

If \(\bar{c}_j = 0\) for non-basic \(x_j\), then \(x_j\) can enter basis without changing objective value.

Degeneracy

A basic feasible solution is degenerate if one or more basic variables have value zero.

  • Causes the same BFS to appear in multiple iterations

  • May lead to cycling (though rare in practice)

  • Identified when RHS = 0 for some basic variable

  • Occurs when there are ties in ratio test

Handling Degeneracy

  • Perturbation methods: Add small \(\epsilon\) to RHS values

  • Bland’s rule: Choose smallest index in case of ties

  • Lexicographic pivoting: More sophisticated tie-breaking

Cycling

  • Theoretical possibility where algorithm cycles indefinitely through same set of BFS

  • Extremely rare in practical problems

  • First demonstrated with Klee-Minty cube (1972)

  • Can occur due to degeneracy and poor pivot selection

Bland’s Anti-Cycling Rule

  • Entering variable: Choose smallest index among candidates with negative reduced costs

  • Leaving variable: Choose smallest index in case of ties in ratio test

  • Guarantee: Finite convergence to optimal solution

Note

While cycling is theoretically possible, it has never been observed in real-world problems using standard pivot rules.

Advanced Topics

Sensitivity Analysis

  • Studies how changes in problem parameters affect the optimal solution

  • Critical for decision-making in uncertain environments

Types of Sensitivity Analysis

  • RHS ranging: How much can \(b_i\) change without changing basis?

  • Objective coefficient ranging: Range for \(c_j\) maintaining optimality

  • Adding new variables: Effect of introducing new decision variables

  • Adding new constraints: Impact of additional restrictions

Shadow Prices (Dual Values)

  • Found in optimal tableau’s \(z\)-row under slack/surplus variables

  • Represent marginal value of resources

  • Indicate maximum amount to pay for additional unit of resource

Duality in Simplex Method

Primal Problem

\[\begin{aligned} \max\quad & c^T x \\ \text{s.t.}\quad & Ax \leq b \\ & x \geq 0 \end{aligned}\]

Dual Problem

\[\begin{aligned} \min\quad & b^T y \\ \text{s.t.}\quad & A^T y \geq c \\ & y \geq 0 \end{aligned}\]

  • Solving primal automatically gives dual solution

  • Weak duality: \(c^T x \leq b^T y\) for all feasible \(x, y\)

  • Strong duality: Optimal values are equal

  • Complementary slackness: \(x_j \bar{c}_j = 0\) and \(y_i s_i = 0\)

Revised Simplex Method

  • More efficient for large, sparse problems

  • Maintains only basis inverse \(B^{-1}\) instead of full tableau

  • Reduces memory requirements significantly

  • Foundation for modern LP solvers

Key Formulas

  • Basic solution: \(x_B = B^{-1}b\)

  • Reduced costs: \(\bar{c}_N = c_N - c_B^T B^{-1} N\)

  • Pivot column: \(\bar{A}_j = B^{-1} A_j\)

  • Basis inverse update: Sherman-Morrison-Woodbury formula

Advantages

  • Numerical stability

  • Memory efficiency

  • Easier to implement sparsity techniques

Computational Aspects

Computational Complexity

Theoretical Complexity

  • Worst case: Exponential time \(O(2^n)\) (Klee-Minty examples)

  • Average case: Polynomial time, typically \(O(m^3)\) per iteration

  • Expected iterations: Usually \(2m\) to \(3m\) iterations for \(m\) constraints

Practical Performance

  • Works excellently for most real-world problems

  • Problems with thousands of variables solved routinely

  • Interior point methods competitive for very large problems

Factors Affecting Performance

  • Problem structure and sparsity

  • Degeneracy level

  • Numerical precision

  • Pivoting strategy

Implementation Considerations

Numerical Issues

  • Floating point errors: Use appropriate tolerance levels

  • Pivot selection: Avoid small pivot elements for stability

  • Scaling: Normalize problem data for better numerical behavior

  • LU factorization: Use for basis inverse computations

Implementation Tips

  • Use sparse matrix techniques for large problems

  • Implement anti-cycling rules for robustness

  • Consider presolve techniques to reduce problem size

  • Monitor condition number of basis matrix

Common Implementation Mistakes

  • Forgetting to check for unboundedness

  • Incorrect ratio test calculations

  • Sign errors in objective function conversion

  • Not handling degeneracy properly

  • Poor pivot element selection

Modern Simplex Variants

Dual Simplex Method

  • Starts with dual feasible but primal infeasible solution

  • Maintains dual feasibility while achieving primal feasibility

  • Useful for sensitivity analysis and reoptimization

  • Complementary to primal simplex method

Network Simplex

  • Specialized for network flow problems

  • Exploits network structure for efficiency

  • Much faster than general simplex for network problems

  • Basis corresponds to spanning tree

Primal-Dual Methods

  • Interior point methods

  • Maintain feasibility for both primal and dual

  • Polynomial time complexity

  • Competitive for very large problems

Applications

Real-World Applications

Business Applications

  • Production planning

  • Resource allocation

  • Portfolio optimization

  • Supply chain management

  • Staff scheduling

Engineering Applications

  • Network design

  • Power generation scheduling

  • Transportation routing

  • Telecommunications optimization

  • Manufacturing processes

Other Fields

Agriculture (crop planning), Economics (equilibrium analysis), Military (logistics), Healthcare (resource allocation)

Case Study: Transportation Problem

Ship products from 3 warehouses to 4 customers:

C1 C2 C3 C4 Supply
W1 8 6 10 9 100
W2 9 12 13 7 150
W3 14 9 16 5 200
Demand 80 120 90 160 450

  • Variables: \(x_{ij}\) = amount shipped from warehouse \(i\) to customer \(j\)

  • Objective: Minimize \(\sum_{i,j} c_{ij} x_{ij}\)

  • Constraints: Supply and demand constraints

  • Creates 12-variable, 7-constraint LP problem

Case Study: Diet Problem

Find minimum cost diet meeting nutritional requirements:

Food Calories Protein Vitamins Cost
Bread 70 3 10 $0.20
Milk 121 8 4 $0.35
Cheese 106 7 7 $0.80
Min Required 350 20 25 -

  • Variables: \(x_1, x_2, x_3\) = servings of bread, milk, cheese

  • Objective: Minimize \(0.20x_1 + 0.35x_2 + 0.80x_3\)

  • Constraints: Nutritional requirements

  • Classic example of linear programming application

Case Study: Production Planning

Company produces two products using three resources:

Resource Product A Product B Available
Labor (hours) 2 3 100
Material (kg) 4 2 120
Machine (hours) 1 2 60
Profit ($) 30 40 -

  • Variables: \(x_1, x_2\) = units of products A and B

  • Objective: Maximize \(30x_1 + 40x_2\)

  • This is exactly our worked example problem!

  • Demonstrates practical relevance of simplex method

Extensions and Variations

Integer Linear Programming

  • Some variables must take integer values

  • Much more difficult than continuous LP

  • Simplex method provides lower bounds

  • Branch-and-bound uses simplex as subroutine

Example

Maximize \(3x_1 + 5x_2\)

Subject to: \(x_1 \leq 4\), \(2x_2 \leq 12\), \(3x_1 + 2x_2 \leq 18\)

\(x_1, x_2 \geq 0\) and integer

LP optimum: \((2, 6)\) with \(z = 36\)

Integer optimum: \((2, 6)\) with \(z = 36\) (lucky case!)

Parametric Linear Programming

  • Study LP problems with parameters

  • Analyze how optimal solution changes with parameters

  • Extension of sensitivity analysis

Example:

Maximize \((3 + \lambda)x_1 + 5x_2\)

Subject to: \(x_1 \leq 4\), \(2x_2 \leq 12\), \(3x_1 + 2x_2 \leq 18\)

Find optimal solution as function of parameter \(\lambda\)

Applications

  • Planning under uncertainty

  • Robust optimization

  • Multi-objective optimization

Stochastic Linear Programming

  • Parameters are random variables

  • Decisions made under uncertainty

  • Two-stage models: some decisions before, others after uncertainty resolves

Approaches

  • Expected value problem: Use expected values of random parameters

  • Chance constraints: Constraints hold with certain probability

  • Recourse models: Corrective actions after uncertainty resolves

Production planning with uncertain demand:

  • First stage: Determine production capacity

  • Second stage: After demand realized, decide actual production

Conclusion

Summary

  • Simplex method efficiently solves LP problems by moving along vertices

  • Systematic tableau approach organizes computations

  • Handles special cases (unbounded, infeasible, multiple optima) systematically

  • Despite exponential worst-case complexity, performs excellently in practice

  • Provides foundation for duality theory and sensitivity analysis

  • Widely applicable across numerous fields and industries

  • Basis for more advanced optimization techniques

Key Takeaways

  1. Always convert to standard form first - ensures systematic approach

  2. Check optimality conditions at each iteration - prevents unnecessary work

  3. Handle special cases appropriately - understand when problems are unbounded/infeasible

  4. Use anti-cycling rules for robustness - Bland’s rule ensures termination

  5. Understand geometric interpretation - helps build intuition

  6. Practice with various examples - builds computational skills

  7. Appreciate dual relationships - provides economic insights

Next Steps in Linear Programming

Advanced Theory

  • Duality theory and economic interpretation

  • Sensitivity analysis and parametric programming

  • Network flow algorithms

  • Interior point methods

Extensions

  • Integer and mixed-integer programming

  • Multi-objective optimization

  • Stochastic programming

  • Robust optimization

Software Tools

  • Commercial solvers: CPLEX, Gurobi, Xpress

  • Open-source: GLPK, CLP, SCIP

  • Modeling languages: AMPL, GAMS, Pyomo

Historical Note and Impact

Historical Development

  • 1947: George Dantzig develops simplex method

  • 1950s: First computer implementations

  • 1970s: Ellipsoid algorithm (first polynomial-time method)

  • 1980s: Interior point methods developed

  • Present: Hybrid methods combining best features

Impact on Society

  • Revolutionary impact on operations research

  • Enabled optimization of large-scale systems

  • Foundation for modern supply chain management

  • Critical for airline scheduling, logistics, finance

  • One of the most important algorithms of 20th century