Introduction to Nonlinear Programming Optimization

What is Optimization?

What is Optimization?

The process of finding the best solution from a set of available alternatives according to some criterion.

Everyday Examples

  • Finding the shortest route to work

  • Maximizing profit while minimizing cost

  • Training a neural network (minimizing loss)

  • Portfolio optimization in finance

Key Question

What makes a problem nonlinear?

General Optimization Problem Formulation

General Optimization Problem

Standard Form

\[\begin{aligned} & \underset{x \in \mathbb{R}^n}{\text{minimize}} & & f(x) \\ & \text{subject to} & & g_i(x) \leq 0, \quad i = 1,\ldots,m \\ & & & h_j(x) = 0, \quad j = 1,\ldots,p \\ & & & x \in \mathcal{X} \end{aligned}\]

  • \(x = (x_1, x_2, \ldots, x_n)^T\): Decision variables

  • \(f(x): \mathbb{R}^n \to \mathbb{R}\): Objective function

  • \(g_i(x) \leq 0\): Inequality constraints

  • \(h_j(x) = 0\): Equality constraints

  • \(\mathcal{X}\): Feasible region/domain

Terminology

Key Definitions

  • Feasible point: \(x\) satisfying all constraints

  • Feasible set: \(\mathcal{F} = \{x : g_i(x) \leq 0, h_j(x) = 0, x \in \mathcal{X}\}\)

  • Optimal solution: \(x^* \in \mathcal{F}\) such that \(f(x^*) \leq f(x)\) \(\forall x \in \mathcal{F}\)

  • Optimal value: \(f^* = f(x^*)\)

Simple Example

\[\begin{aligned} \min_{x \in \mathbb{R}} \quad & x^2 + 2x + 1 \\ \text{s.t.} \quad & x \geq 0 \end{aligned}\]
What is \(x^*\) and \(f^*\)?

Linear vs. Nonlinear Optimization

Linear Programming (LP)

Linear Program

\[\begin{aligned} & \min_{x} & & c^T x \\ & \text{s.t.} & & Ax \leq b \\ & & & Ex = d \\ & & & x \geq 0 \end{aligned}\]

  • Objective function is linear

  • All constraints are linear

  • Feasible region is a polyhedron

  • Global optimum always exists (if bounded)

  • Polynomial-time solvable (Simplex, Interior Point)

Nonlinear Programming (NLP)

Nonlinear Program

At least one of \(f(x)\), \(g_i(x)\), or \(h_j(x)\) is nonlinear

Aspect Linear Nonlinear
Objective \(c^T x\) \(x^2 + \sin(x)\)
Constraints \(Ax \leq b\) \(x_1^2 + x_2^2 \leq 1\)
Feasible region Polyhedron Curved boundaries
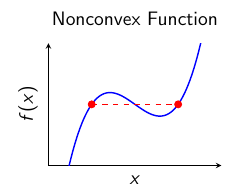
Optima Single global Multiple local
Complexity Polynomial Generally NP-hard
Algorithms Simplex, IPM Gradient-based

Why Nonlinear Optimization is Challenging

  • Multiple local optima

  • No polynomial-time guarantee

  • Sensitivity to starting point

  • Convergence issues

  • Constraint qualification

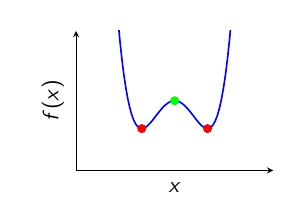
multiple local minima
Multiple local minima

Types of Nonlinear Problems

Classification of NLP Problems

By Constraints

  • Unconstrained: \(\min f(x)\)

  • Equality constrained: \(\min f(x)\) s.t. \(h(x) = 0\)

  • Inequality constrained: \(\min f(x)\) s.t. \(g(x) \leq 0\)

  • Mixed: Both equality and inequality constraints

By Function Properties

  • Smooth: \(f, g, h\) are continuously differentiable

  • Nonsmooth: Contains non-differentiable points

  • Convex: Special structure (global optimum guaranteed)

  • Nonconvex: General case (local optima possible)

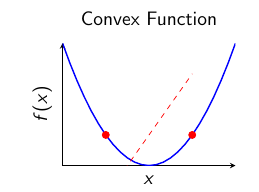
Convexity - A Crucial Concept

Convex Sets and Functions

A set \(S\) is convex if for any \(x, y \in S\) and \(\lambda \in [0,1]\):

\[\lambda x + (1-\lambda)y \in S\]

\(f\) is convex if for any \(x, y \in \text{dom}(f)\) and \(\lambda \in [0,1]\):

\[f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y)\]

Golden Rule

Convex problem = Convex objective + Convex feasible set

\(\Rightarrow\) Every local minimum is a global minimum!

Visual Understanding of Convexity

Secant line above function
Secant line above function
Secant line below function
Secant line below function

Applications of Nonlinear Optimization

Real-World Applications

Engineering & Design

  • Structural optimization

  • Control system design

  • Signal processing

  • Robotics path planning

Machine Learning & AI

  • Neural network training

  • Support vector machines

  • Reinforcement learning

  • Computer vision

Economics & Finance

  • Portfolio optimization

  • Risk management

  • Option pricing

  • Resource allocation

Operations Research

  • Supply chain optimization

  • Facility location

  • Energy systems

  • Telecommunications

Case Study: Portfolio Optimization

Markowitz Mean-Variance Model

\[\begin{aligned} & \min_{w} & & \frac{1}{2} w^T \Sigma w \\ & \text{s.t.} & & \mu^T w \geq r_{\min} \\ & & & \mathbf{1}^T w = 1 \\ & & & w \geq 0 \end{aligned}\]

  • \(w\): Portfolio weights

  • \(\Sigma\): Covariance matrix (risk)

  • \(\mu\): Expected returns

  • \(r_{\min}\): Minimum required return

Why nonlinear? Quadratic objective function!

Solution Approaches - Preview

Solution Methodologies

Analytical Approaches

  • Optimality conditions (KKT conditions)

  • Lagrange multipliers

  • Convex analysis

Numerical Methods

  • Gradient-based: Steepest descent, Newton’s method

  • Constrained: Sequential quadratic programming

  • Global: Genetic algorithms, simulated annealing

  • Modern: Interior point methods, trust region

Historical Perspective

Historical Development

  • 1600s-1700s: Newton, Leibniz, Euler (calculus of variations)

  • 1800s: Lagrange multipliers, method of Lagrange

  • 1939: Karush develops optimality conditions

  • 1947: Dantzig invents Simplex method (Linear Programming)

  • 1951: Kuhn-Tucker extend Karush conditions (KKT)

  • 1960s-1980s: Development of nonlinear programming algorithms

  • 1990s-Present: Interior point methods, convex optimization

  • 2000s-Present: Large-scale optimization, machine learning applications

Practical Considerations

Key Challenges in Practice

  • Scaling: How to handle large-scale problems?

  • Initialization: Where to start the algorithm?

  • Convergence: When to stop?

  • Globalization: How to avoid local optima?

  • Numerical stability: Dealing with ill-conditioning

Success Factors

  • Understanding problem structure

  • Choosing appropriate algorithms

  • Proper implementation and tuning

Summary

  • Nonlinear optimization is everywhere in science and engineering

  • Key difference from linear: local vs global optima

  • Convexity is a game-changer when present

  • Multiple solution approaches exist

  • Rich mathematical theory supports practical algorithms

Next: Mathematical Foundations & Convex Analysis