Mathematical Foundations for Nonlinear Programming Optimization

Review of Multivariable Calculus

Multivariable Calculus Essentials

Key Objects in Optimization

For a function \(f: \mathbb{R}^n \to \mathbb{R}\):

  • Partial derivative: \(\frac{\partial f}{\partial x_i}\) - rate of change w.r.t. \(x_i\)

  • Gradient: \(\nabla f(x) = \left[\frac{\partial f}{\partial x_1}, \dots, \frac{\partial f}{\partial x_n}\right]^T\)

  • Hessian: \(\nabla^2 f(x)_{ij} = \frac{\partial^2 f}{\partial x_i \partial x_j}\)

Example

For \(f(x,y) = x^2 + 2xy + y^3\):

\[\nabla f = \begin{bmatrix} 2x + 2y \\ 2x + 3y^2 \end{bmatrix}, \quad \nabla^2 f = \begin{bmatrix} 2 & 2 \\ 2 & 6y \end{bmatrix}\]

Partial Derivatives - Geometric Interpretation

  • \(\frac{\partial f}{\partial x_i}\) measures rate of change along \(x_i\)-axis

  • Keep all other variables constant

  • Slope of tangent line to curve \(f(x_1, \ldots, x_i, \ldots, x_n)\)

Partial derivatives
Partial derivatives

Chain Rule (Multivariate)

If \(f(x(t), y(t))\), then:

\[\frac{df}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}\]

Gradients, Hessians & Jacobians

Gradient: Directional Steepest Ascent

  • Points in direction of maximum increase of \(f\)

  • Orthogonal to level sets (\(\nabla f \perp \{x \mid f(x)=c\}\))

  • Critical point: \(\nabla f(x^*) = 0\)

  • Magnitude: \(\|\nabla f(x)\|\) = maximum directional derivative

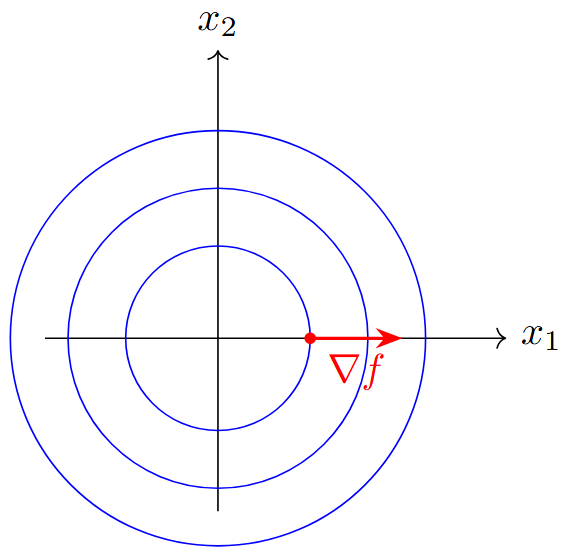
Directional steepest ascent
Directional steepest ascent

Directional Derivative

Along unit vector \(d\):

\[D_d f(x) = \nabla f(x)^T d = \|\nabla f(x)\| \cos \theta\]

Hessian Matrix: Second-Order Information

Definition

\[\nabla^2 f(x) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}\]

  • Symmetric (if \(f \in C^2\)): \(\frac{\partial^2 f}{\partial x_i \partial x_j} = \frac{\partial^2 f}{\partial x_j \partial x_i}\)

  • Determines curvature of \(f\)

  • Used in optimality conditions and Newton’s method

Jacobian: Vector-Valued Functions

For \(F: \mathbb{R}^n \to \mathbb{R}^m\) with \(F(x) = [F_1(x), F_2(x), \ldots, F_m(x)]^T\):

\[J_F(x) = \begin{bmatrix} \frac{\partial F_1}{\partial x_1} & \cdots & \frac{\partial F_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial F_m}{\partial x_1} & \cdots & \frac{\partial F_m}{\partial x_n} \end{bmatrix}\]

Example

\[\begin{aligned} \text{For}~F(x,y) &= \begin{bmatrix} x^2y \\ \sin(x+y) \\ e^{xy} \end{bmatrix}: \\ J_F &= \begin{bmatrix} 2xy & x^2 \\ \cos(x+y) & \cos(x+y) \\ ye^{xy} & xe^{xy} \end{bmatrix} \end{aligned}\]

Note: When \(m=1\), \(J_F = \nabla F^T\)

Taylor Series Approximations

Taylor’s Theorem in \(\mathbb{R}^n\)

Theorem: First-Order Approximation

For \(f \in C^1\):

\[f(x + \Delta x) \approx f(x) + \nabla f(x)^T \Delta x\]

Theorem : Second-Order Approximation

For \(f \in C^2\):

\[f(x + \Delta x) \approx f(x) + \nabla f(x)^T \Delta x + \frac{1}{2} \Delta x^T \nabla^2 f(x) \Delta x\]

Error Analysis

  • First-order error: \(O(\|\Delta x\|^2)\)

  • Second-order error: \(O(\|\Delta x\|^3)\)

Why Taylor Series Matter in Optimization

Algorithm Design Foundation

  • Gradient descent: Uses 1st-order approximation

  • Newton’s method: Uses 2nd-order approximation

  • Quasi-Newton methods: Approximate 2nd-order info

Example: Quadratic Model

At each iteration, approximate \(f\) by quadratic:

\[q(s) = f(x_k) + \nabla f(x_k)^T s + \frac{1}{2} s^T B_k s\]
where \(B_k \approx \nabla^2 f(x_k)\)

Local vs. Global Behavior

Taylor approximations are local - accuracy decreases with distance from expansion point

Convex Analysis

Convex Sets and Their Properties

Definition : Convex Set

A set \(S \subseteq \mathbb{R}^n\) is convex if:

\[\forall x, y \in S, \forall \lambda \in [0,1]: \lambda x + (1-\lambda) y \in S\]

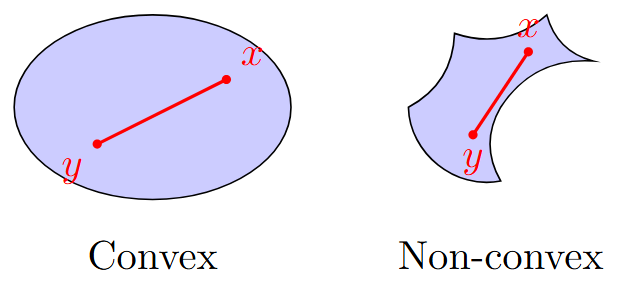
Convex and non-convex
Convex and non-convex

Examples of Convex Sets

  • Hyperplanes: \(\{x \mid a^T x = b\}\)

  • Half-spaces: \(\{x \mid a^T x \leq b\}\)

  • Balls: \(\{x \mid \|x - c\| \leq r\}\)

  • Intersection of convex sets is convex

Convex Functions

A function \(f: S \to \mathbb{R}\) on convex set \(S\) is convex if:

\[\forall x, y \in S, \forall \lambda \in [0,1]: f(\lambda x + (1-\lambda) y) \leq \lambda f(x) + (1-\lambda) f(y)\]
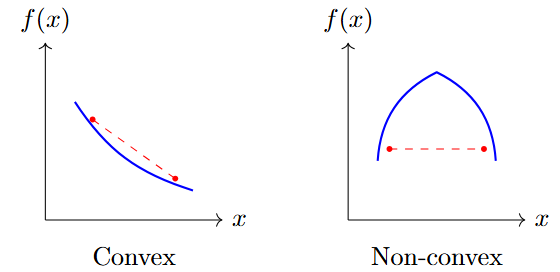
Convex and non-convex
Convex and non-convex

Strictly Convex

If inequality is strict for \(x \neq y\) and \(\lambda \in (0,1)\)

Characterizations of Convex Functions

First-Order Condition

For \(f \in C^1\) on convex set \(S\), \(f\) is convex iff:

\[f(y) \geq f(x) + \nabla f(x)^T (y-x) \quad \forall x,y \in S\]

Theorem (Second-Order Condition)

For \(f \in C^2\) on convex set \(S\), \(f\) is convex iff:

\[\nabla^2 f(x) \succeq 0 \quad \forall x \in S\]

(Hessian is positive semidefinite)

Key Insight

Convex functions have no local minima that are not global

Properties of Convex Functions

Preservation Under Operations

  • Positive combination: \(\alpha f + \beta g\) convex if \(\alpha, \beta \geq 0\)

  • Pointwise maximum: \(\max\{f_1(x), f_2(x), \ldots\}\) convex

  • Composition: \(g(f(x))\) convex if \(g\) convex increasing, \(f\) convex

Example (Common Convex Functions)

  • Linear: \(a^T x + b\)

  • Quadratic: \(\frac{1}{2}x^T Q x + q^T x + r\) (if \(Q \succeq 0\))

  • Exponential: \(e^{ax}\)

  • Norms: \(\|x\|_p\) for \(p \geq 1\)

  • Logarithmic barrier: \(-\sum_{i=1}^n \log(x_i)\) on \(\{x \mid x > 0\}\)

Optimality Conditions

Unconstrained Optimality Conditions

Problem

\[\min_{x \in \mathbb{R}^n} f(x)\]

Theorem (First-Order Necessary Condition (FONC))

If \(x^*\) is a local minimum and \(f \in C^1\), then:

\[\nabla f(x^*) = 0\]

Theorem (Second-Order Necessary Condition (SONC))

If \(x^*\) is a local minimum and \(f \in C^2\), then:

\[\nabla f(x^*) = 0 \quad \text{and} \quad \nabla^2 f(x^*) \succeq 0\]

Critical Points

Points where \(\nabla f(x) = 0\) - could be minima, maxima, or saddle points

Sufficient Conditions

Theorem: (Second-Order Sufficient Condition (SOSC))

If \(\nabla f(x^*) = 0\) and \(\nabla^2 f(x^*) \succ 0\), then \(x^*\) is a strict local minimum.

Classification of Critical Points

  • \(\nabla^2 f \succ 0\): Local minimum

  • \(\nabla^2 f \prec 0\): Local maximum

  • \(\nabla^2 f\) indefinite: Saddle point

  • \(\nabla^2 f\) singular: Inconclusive

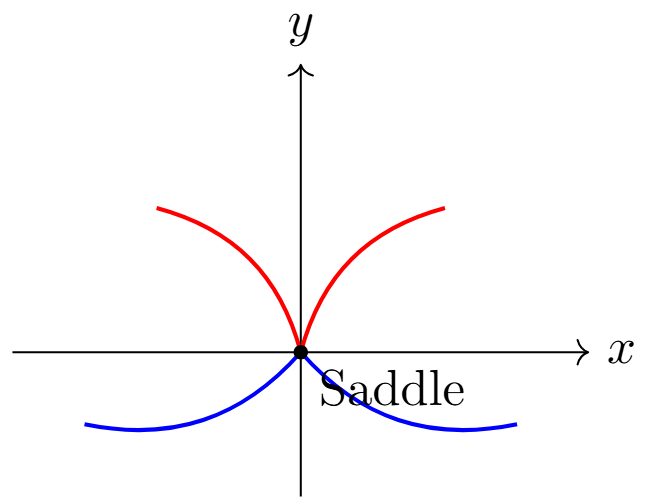
Example

For \(f(x,y) = x^2 - y^2\): \(\nabla f = [2x, -2y]^T\), \(\nabla^2 f = \begin{bmatrix} 2 & 0 \\ 0 & -2 \end{bmatrix}\)

At \((0,0)\): \(\nabla f = 0\), but \(\nabla^2 f\) is indefinite \(\Rightarrow\) saddle point

Necessary vs. Sufficient Conditions

Necessary Conditions

  • Must hold at optimum

  • Help find candidates

  • Not sufficient for optimality

Example

\(f(x) = x^4\) at \(x=0\):

  • \(f'(0) = 0\) \(\checkmark\)

  • \(f''(0) = 0\) (inconclusive)

  • But \(x=0\) is global minimum!

Sufficient Conditions

  • Guarantee optimality

  • Help verify candidates

  • Often stronger than necessary

Gap Between Necessary and Sufficient

There exist points satisfying necessary conditions but not sufficient conditions that are still optimal.

Introduction to Lagrange Multipliers

Constrained Optimization Setup

Problem (Equality Constrained Problem)

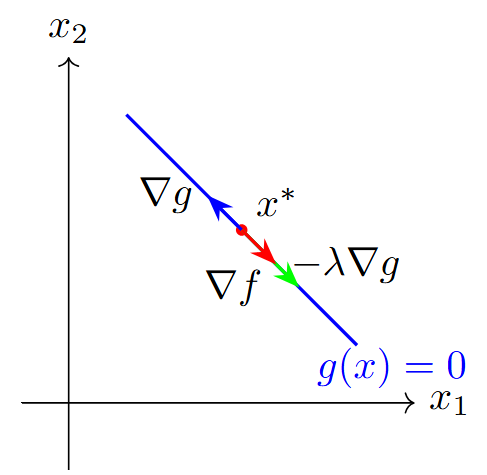
\[\begin{aligned} \min_{x \in \mathbb{R}^n} &\quad f(x) \\ \text{subject to} &\quad g_i(x) = 0, \quad i = 1, 2, \ldots, m \end{aligned}\]

Key Insight

At optimum, gradient of objective must be orthogonal to feasible directions

At optimum \(x^*\):

  • \(\nabla f(x^*)\) parallel to \(\nabla g(x^*)\)

  • Both orthogonal to constraint

  • Feasible directions have zero projection on \(\nabla f\)

Lagrange Multiplier Theorem

Theorem: First-Order Necessary Conditions

Let \(x^*\) be a local minimum of \(f(x)\) subject to \(g_i(x) = 0\), \(i = 1, \ldots, m\). If \(\nabla g_1(x^*), \ldots, \nabla g_m(x^*)\) are linearly independent, then there exist multipliers \(\lambda_1^*, \ldots, \lambda_m^*\) such that:

\[\nabla f(x^*) + \sum_{i=1}^m \lambda_i^* \nabla g_i(x^*) = 0\]

Lagrangian Function

\[L(x, \lambda) = f(x) + \sum_{i=1}^m \lambda_i g_i(x)\]

KKT System

\[\begin{aligned} \nabla_x L(x^*, \lambda^*) &= 0 \quad \text{(stationarity)} \\ g_i(x^*) &= 0 \quad \text{(feasibility)} \end{aligned}\]

Geometric Interpretation

  • \(\lambda_i^*\) measures sensitivity of optimal value to constraint \(i\)

  • \(\lambda_i^* > 0\): constraint "pushes" solution away from unconstrained optimum

  • \(\lambda_i^* < 0\): constraint "pulls" solution toward unconstrained optimum

Economic Interpretation

\(\lambda_i^*\) = shadow price of constraint \(i\)

\[\lambda_i^* \approx \frac{\partial f^*}{\partial b_i}\]

where \(g_i(x) = b_i\) (perturbed constraint)

Simple Example: Lagrange Multipliers

Example

Minimize \(f(x,y) = x^2 + y^2\) subject to \(g(x,y) = x + y - 1 = 0\)

Solution:

  1. Form Lagrangian: \(L(x,y,\lambda) = x^2 + y^2 + \lambda(x + y - 1)\)

  2. KKT conditions:

    \[\begin{aligned} \frac{\partial L}{\partial x} &= 2x + \lambda = 0 \\ \frac{\partial L}{\partial y} &= 2y + \lambda = 0 \\ \frac{\partial L}{\partial \lambda} &= x + y - 1 = 0 \end{aligned}\]

  3. Solve: From (1) and (2): \(x = y = -\frac{\lambda}{2}\)

  4. Substitute into (3): \(-\frac{\lambda}{2} - \frac{\lambda}{2} - 1 = 0 \Rightarrow \lambda = -1\)

  5. Therefore: \(x^* = y^* = \frac{1}{2}\), \(f^* = \frac{1}{2}\)

Preview: Inequality Constraints

Problem (General Nonlinear Program)

\[\begin{aligned} \min_{x \in \mathbb{R}^n} &\quad f(x) \\ \text{subject to} &\quad g_i(x) = 0, \quad i \in \mathcal{E} \\ &\quad g_j(x) \leq 0, \quad j \in \mathcal{I} \end{aligned}\]

Karush-Kuhn-Tucker (KKT) Conditions

At optimal point \((x^*, \lambda^*, \mu^*)\):

\[\begin{aligned} \nabla f(x^*) + \sum_{i \in \mathcal{E}} \lambda_i^* \nabla g_i(x^*) + \sum_{j \in \mathcal{I}} \mu_j^* \nabla g_j(x^*) &= 0 \\ g_i(x^*) &= 0, \quad i \in \mathcal{E} \\ g_j(x^*) &\leq 0, \quad j \in \mathcal{I} \\ \mu_j^* &\geq 0, \quad j \in \mathcal{I} \\ \mu_j^* g_j(x^*) &= 0, \quad j \in \mathcal{I} \quad \text{(complementarity)} \end{aligned}\]

Next lecture: Detailed KKT analysis and constraint qualifications

Key Takeaways

  1. Calculus Tools: Gradients, Hessians, Jacobians are fundamental

  2. Taylor Approximations: Foundation for iterative algorithms

  3. Convexity: Guarantees global optimality of local solutions

  4. Optimality Conditions:

    • Necessary: Must hold at optimum (help find candidates)

    • Sufficient: Guarantee optimality (help verify candidates)

  5. Lagrange Multipliers: Handle equality constraints elegantly

Mathematical Foundation Complete

We now have the mathematical tools to tackle general nonlinear optimization problems!

Next lecture: KKT conditions and constraint qualifications

Practice Problems

  1. Compute gradient and Hessian of \(f(x,y,z) = x^2y + e^{yz} + \sin(xz)\)

  2. Show that \(f(x) = \|x\|_2^2\) is convex using second-order conditions

  3. Find all critical points of \(f(x,y) = x^3 - 3xy^2 + y^3\) and classify them

  4. Use Lagrange multipliers to minimize \(f(x,y) = xy\) subject to \(x^2 + y^2 = 1\)

  5. Prove that the intersection of two convex sets is convex