Introduction to Engineering Optimization: Fundamentals and Applications

Why Study Optimization?

Why Study Optimization?

A Motivating Question

How can we design a bridge that is strong, cost-effective, and sustainable under strict constraints?

  • Optimization answers such questions by finding the best solution.

  • It’s the backbone of engineering innovation across disciplines.

  • This course will equip you to tackle real-world engineering challenges.

Course Overview

Course Objectives

  • Understand fundamental concepts of optimization in engineering.

  • Formulate engineering problems as mathematical optimization problems.

  • Explore classical and modern optimization techniques.

  • Apply optimization to real-world engineering scenarios.

  • Develop computational skills to implement optimization algorithms.

Introduction

What is Optimization?

Definition

Optimization is the process of finding the best feasible solution under given constraints to minimize cost or maximize benefit.

  • Core to engineering design and decision-making.

  • Applies to planning, operations, and maintenance.

  • Enables transformation between maximization and minimization.

Minimizing \(f(x)\) is equivalent to maximizing \(-f(x)\).
Minimizing \(f(x)\) is equivalent to maximizing \(-f(x)\).

Why Optimization Matters

  • Resource Efficiency: Minimize material, energy, and costs.

  • Performance: Maximize reliability, output, and safety.

  • Competitive Edge: Faster development, superior products.

  • Sustainability: Reduce waste and environmental impact.

Real-World Impact Optimizing an aircraft wing design by 1% can save millions in fuel costs annually.

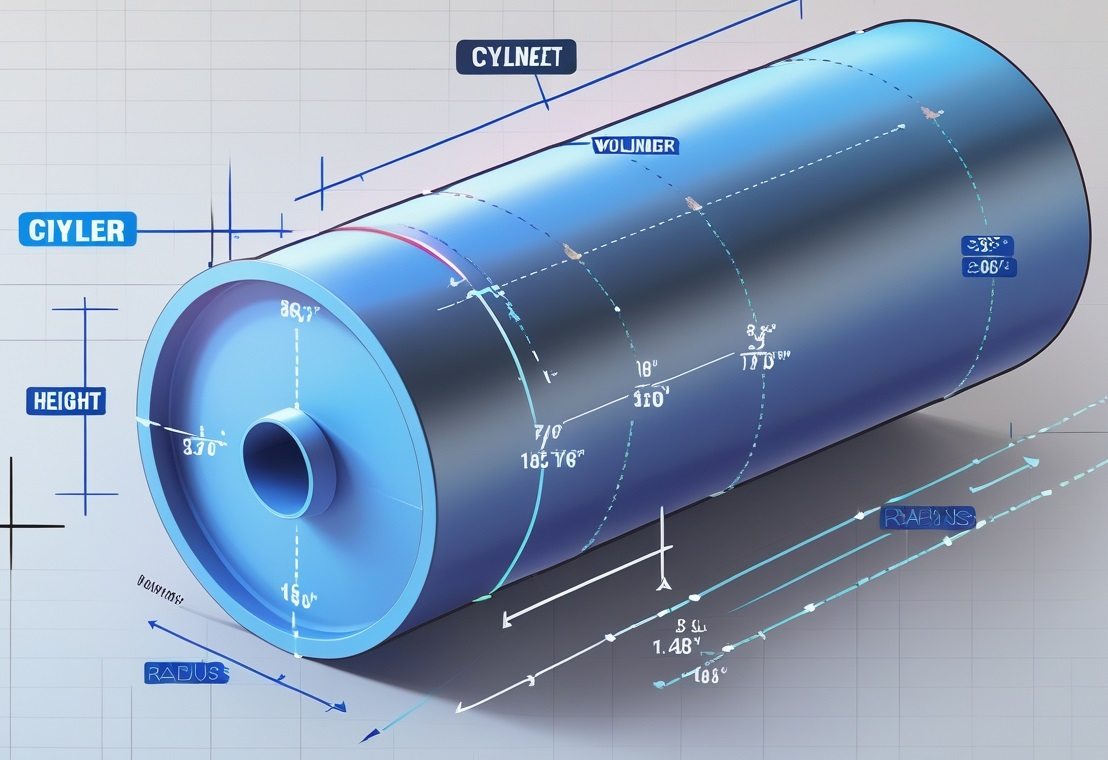
A Simple Example: Minimizing Material Cost

Problem

Design a cylindrical container to hold 1 liter with minimal surface area (material cost).

  • Design Variables: Radius (\(r\)), Height (\(h\)).

  • Objective: Minimize surface area \(A = 2\pi r h + 2\pi r^2\).

  • Constraint: Volume \(V = \pi r^2 h = 1000 \, \text{cm}^3\).

Optimal cylinder dimensions.
Optimal cylinder dimensions.

Key Concepts

Components of an Optimization Problem

  1. Design Variables: Parameters to optimize (e.g., dimensions, settings).

  2. Objective Function: Quantity to minimize/maximize (e.g., cost, efficiency).

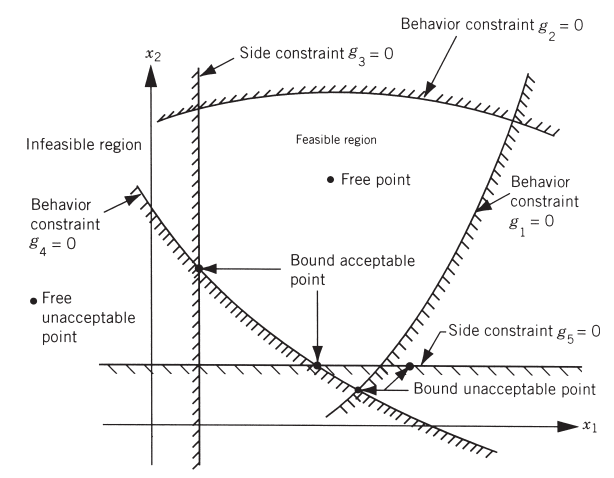
  3. Constraints: Limits on variables (e.g., physical, economic).

  4. Feasible Region: Set of solutions satisfying all constraints.

Standard Formulation
\[ \text{Find } \mathbf{X} = \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} \text{ that minimizes } f(\mathbf{X}) \] Subject to: \[ g_j(\mathbf{X}) \leq 0, \quad l_k(\mathbf{X}) = 0, \quad x_i^L \leq x_i \leq x_i^U \]

Properties of Objective Functions

  • Invariance: Optimum unchanged by:

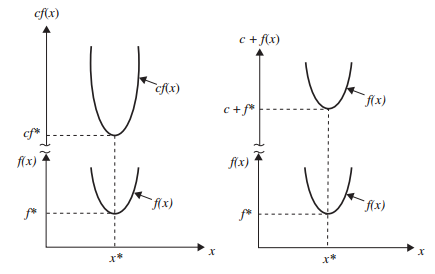
    • Positive scaling: \(f(x)\) vs. \(c f(x)\), \(c > 0\).

    • Positive translation: \(f(x)\) vs. \(c + f(x)\).

    Optimum solution of \(cf (x)\) or \(c + f (x)\) same as that of \(f (x)\).
    Optimum solution of \(cf (x)\) or \(c + f (x)\) same as that of \(f (x)\).

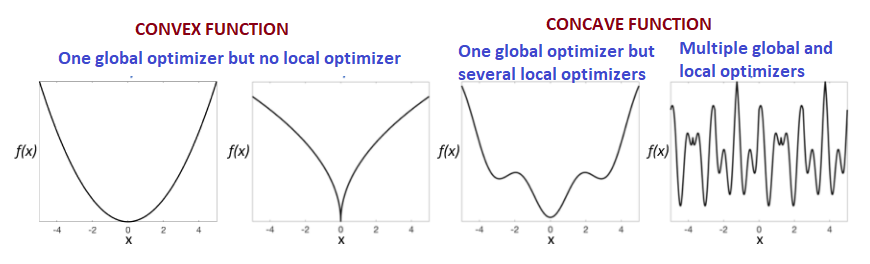
  • Convexity: Ensures global optimality for convex problems.

  • Differentiability: Determines suitable optimization methods.

  • Multi-Modality: Multiple local optima may exist in non-convex problems.

Convex vs. non-convex objective functions.
Convex vs. non-convex objective functions.

Historical Development

Evolution of Optimization

  • 17th-18th Century:

    • Newton (1660s): Calculus for extrema.

    • Lagrange (1788): Lagrange multipliers.

  • 1940s-60s:

    • Dantzig (1947): Linear programming.

    • Bellman (1957): Dynamic programming.

  • 1970s-90s:

    • Holland (1975): Genetic algorithms.

    • Kirkpatrick (1983): Simulated annealing.

  • 2000s-Present:

    • Kennedy (1995): Particle swarm optimization.

    • Machine learning-integrated methods.

Problem Classification

Types of Optimization Problems

Classification of Optimization Problems
Criterion Types
Variables Continuous, Discrete, Mixed
Constraints Constrained, Unconstrained
Linearity Linear, Nonlinear
Objectives Single, Multi-Objective
Determinism Deterministic, Stochastic

Optimization Algorithms

  • Optimization problems are solved iteratively, progressively improving the solution.

  • Common optimization algorithms include:

    • Coordinate descent

    • Gradient (steepest) descent

    • Conjugate gradients

    • Newton’s method and variants

    • Stochastic gradient descent

  • Choosing an algorithm involves a trade-off between:

    • Complexity of each iteration

    • Number of iterations needed to converge

Optimization Methods Landscape

Classical Methods

  • Calculus-based (e.g., Gradient Descent)

  • Linear Programming

  • Nonlinear Programming

  • Dynamic Programming

  • Kuhn-Tucker Conditions

Modern Methods

  • Genetic Algorithms

  • Particle Swarm Optimization

  • Simulated Annealing

  • Ant Colony Optimization

  • Neural Network-based Methods

Challenges

Challenges in Optimization

  • Complexity: Large-scale problems with many variables.

  • Non-Convexity: Multiple local optima can mislead algorithms.

  • Constraints: Balancing feasibility and optimality.

  • Computational Cost: Time-intensive for real-time applications.

  • Uncertainty: Handling stochastic or incomplete data.

Example Optimizing a supply chain with uncertain demand requires stochastic methods.

Applications

Applications Across Engineering

  • Mechanical:

    • Gear and mechanism design.

    • Thermal system optimization.

    • Robot motion planning.

  • Civil:

    • Structural design (e.g., bridges).

    • Transportation networks.

    • Water resource management.

  • Electrical:

    • Circuit optimization.

    • Power grid efficiency.

    • Control system tuning.

  • Chemical:

    • Process optimization.

    • Reactor design.

    • Mixing and separation processes.

Solution Approach

Optimization Process Flow

  1. Problem Identification: Define the engineering problem.

  2. Mathematical Formulation: Express as an optimization problem.

  3. Method Selection: Choose appropriate algorithm.

  4. Implementation: Code or use software tools.

  5. Validation: Verify solution accuracy.

  6. Deployment: Apply to real-world system.

Design space with feasible region.
Design space with feasible region.

Conclusion

Summary and Next Steps

  • Optimization is critical for efficient, high-performance engineering.

  • Requires precise problem formulation and method selection.

  • Spans classical to modern techniques with diverse applications.

  • Next lectures: Dive into mathematical foundations and specific algorithms.

Takeaway

Optimization empowers engineers to design better, smarter, and sustainable solutions.