Introduction to Potential and Electric Field

Fundamental Concepts: Potential and Electric Field

Key Relationships

Potential is fundamental for understanding electrostatic fields
Electric field intensity from potential:
\[\boxed{\mathbf{E} = -\nabla V}\]
Electric flux density from field intensity:
\[\boxed{\mathbf{D} = \epsilon \mathbf{E}}\]
Volume charge density from flux density:
\[\boxed{\nabla \cdot \mathbf{D} = \rho_v}\]

Challenge

Exact charge distribution for a given potential is often unknown

Governing Equations: Poisson’s and Laplace’s

Substituting relationships into Gauss’s law:
\[\begin{aligned} \nabla \cdot \mathbf{D} &= \rho_v \\ \nabla \cdot (\epsilon \mathbf{E}) &= \rho_v \\ -\nabla \cdot (\epsilon \nabla V) &= \rho_v \end{aligned}\]
For constant permittivity \(\epsilon\):
\[\boxed{\nabla^2 V = -\frac{\rho_v}{\epsilon}} \Leftarrow \quad {\color{blue}{\text{Poisson's equation}}}\]

Special Case

In HV equipment, space charges are often absent (\(\rho_v = 0\))

\[\boxed{\nabla^2 V = 0}\]

Laplace’s equation

Note: \(\rho_v = 0\) allows singular charges (point, line, surface)

Mathematical Tools: Del Operator

Del Operator in Cartesian Coordinates

\[\nabla = \frac{\partial}{\partial x}\hat{\mathbf{i}} + \frac{\partial}{\partial y}\hat{\mathbf{j}} + \frac{\partial}{\partial z}\hat{\mathbf{k}}\]

Laplace’s Equation (3D Cartesian)

\[\nabla^2 V = \frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} + \frac{\partial^2 V}{\partial z^2} = 0\]

\(\nabla^2 V\) is a scalar quantity
Forms the basis for all numerical methods discussed

Solution Methods for Potential Distribution

Numerical Methods

Finite Difference Method (FDM)
- Grid-based approach
- Simple implementation
Finite Element Method (FEM)
- Energy minimization
- Complex geometries
Charge Simulation Method (CSM)
- Fictitious charges
- Fast computation
Surface Charge Simulation (SCSM)
- Surface charge density
- High accuracy

Experimental Method

Electrolytic Tank Method
- Analog simulation
- 2D/3D field mapping
- Historical importance

Selection Criteria

Geometry complexity
Computational resources
Required accuracy
Time constraints

Finite Difference Method (FDM)

FDM: Basic Principles

Approach

Solves Laplace’s equation in charge-free regions
2D analysis for simplicity (x-y plane)
Uniform grid discretization (spacing \(h\))
Central difference approximation

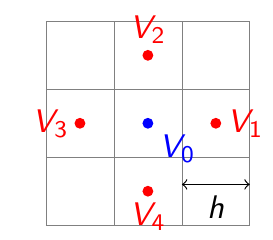
Convex vs. non-convex functions and sets. — FDM 5-point stencil.

Governing Equation

For 2D fields:

\[\frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} = 0\]

FDM: Mathematical Derivation

Finite Difference Approximations

First derivatives at midpoints (a and c):

\[\begin{aligned} \left.\frac{\partial V}{\partial x}\right|_a &\approx \frac{V_1 - V_0}{h} \\ \left.\frac{\partial V}{\partial x}\right|_c &\approx \frac{V_0 - V_3}{h} \end{aligned}\]

Second Derivatives

\[\begin{aligned} \frac{\partial^2 V}{\partial x^2}\Big|_0 &\approx \frac{V_1 + V_3 - 2V_0}{h^2} \\ \frac{\partial^2 V}{\partial y^2}\Big|_0 &\approx \frac{V_2 + V_4 - 2V_0}{h^2} \end{aligned}\]

Key Result

Substituting into Laplace’s equation:

\[\boxed{V_0 = \frac{1}{4}(V_1 + V_2 + V_3 + V_4)}\]

Potential at any node equals the average of its four neighbors

FDM: Boundary Conditions and Solution

Boundary Conditions

Dirichlet: Fixed potential \(V\)
- Applied to electrodes
- Known voltage values
Neumann: Zero normal derivative
- \(\frac{\partial V}{\partial n} = 0\)
- Symmetry planes

Solution Methods

Iterative Methods
- Gauss-Seidel
- Successive Over-Relaxation (SOR)
- Point-by-point updates
Direct Methods
- Matrix inversion
- Computationally expensive

Convergence

Smaller grid spacing \(h\) improves accuracy but increases computational cost

FDM: Applications and Limitations

Applications

Best suited for:
- 2D symmetrical fields
- Regular geometries
- Simple boundary conditions
Used in electromagnetics, heat transfer, fluid dynamics

Limitations

Challenges with:
- Irregular 3D fields
- Complex boundaries
- Non-uniform grids
Large memory requirements
Less flexible than FEM

Improvements

Adaptive mesh refinement
Multigrid methods
Non-uniform grid spacing

Finite Element Method (FEM)

FEM: Fundamental Principle

Energy-Based Approach

Not a direct solution of Laplace’s equation
Based on energy minimization principle
Voltage distribution that minimizes total energy satisfies boundary conditions

Energy Density

Energy per unit volume in electrostatic field:

\[W_{vol} = \frac{1}{2}\epsilon |\mathbf{E}|^2 = \frac{1}{2}\epsilon |\nabla V|^2\]

Total Energy

For the entire field region:

\[W = \int_V \frac{1}{2}\epsilon |\nabla V|^2 \, dv\]

Variational Principle

The potential \(V\) that minimizes \(W\) satisfies \(\nabla^2 V = 0\)

FEM: Energy Formulation

3D Energy Expression

\[W = \frac{1}{2}\epsilon \iiint \left[\left(\frac{\partial V}{\partial x}\right)^2 + \left(\frac{\partial V}{\partial y}\right)^2 + \left(\frac{\partial V}{\partial z}\right)^2\right] dx\,dy\,dz\]

2D Energy per Unit Length

For 2D fields (\(\frac{\partial V}{\partial z} = 0\)):

\[W_A = z \iint \frac{1}{2}\epsilon \left[\left(\frac{\partial V}{\partial x}\right)^2 + \left(\frac{\partial V}{\partial y}\right)^2\right] dx\,dy\]

Assumptions

Isotropic dielectric material
No space charge (\(\rho_v = 0\))
Fixed potential at electrode boundaries

FEM: Discretization Strategy

Element Types

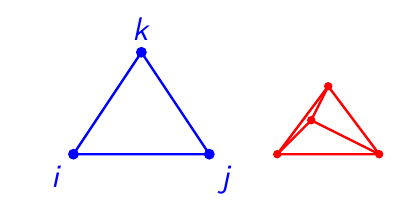
2D: Triangular elements
3D: Tetrahedral elements
Higher-order elements possible

Mesh Considerations

Refinement in high-gradient regions
Corners and edges need fine mesh
Adaptive meshing for optimal accuracy

FEM: Element Formulation

Linear Approximation Within Element

For triangular element with nodes \(i\), \(j\), \(k\):

\[V(x,y) = a_1 + a_2 x + a_3 y\]

Nodal Relationships

\[\begin{bmatrix} V_i \\ V_j \\ V_k \end{bmatrix} = \begin{bmatrix} 1 & x_i & y_i \\ 1 & x_j & y_j \\ 1 & x_k & y_k \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix}\]

Key Properties

Linear potential variation within element
Constant electric field within element
Shape functions interpolate between nodal values
Higher-order elements provide better accuracy

FEM: System Assembly and Solution

Element Stiffness Matrix

For element \(e\):

\[_e = \frac{\epsilon}{4\Delta_e} \begin{bmatrix} \beta_i^2+\gamma_i^2 & \beta_i\beta_j+\gamma_i\gamma_j & \beta_i\beta_k+\gamma_i\gamma_k \\ \text{symmetric} & \beta_j^2+\gamma_j^2 & \beta_j\beta_k+\gamma_j\gamma_k \\ & & \beta_k^2+\gamma_k^2 \end{bmatrix}_e\]

Global System

\[ [C][V] = [Q]\]

where \([C]\) is assembled from element matrices \([C]_e\)

Solution Methods

Direct: Matrix factorization (LU, Cholesky)
Iterative: Conjugate gradient, GMRES
Optimization: Fletcher-Powell for energy minimization

FEM: Boundary Conditions and Applications

Boundary Conditions

Dirichlet: \(V = V_0\) (electrodes)
Neumann: \(\frac{\partial V}{\partial n} = 0\) (symmetry)
Mixed: Combination of both

Applications

Complex geometries
Curved/thin electrodes
Composite dielectrics
2D and weakly non-uniform 3D fields

Advantages

High accuracy
Flexible meshing
Complex boundaries
Well-established theory

Limitations

High computational cost for 3D
Mesh quality critical
Memory intensive
Setup complexity

Charge Simulation Method (CSM)

CSM: Basic Principle

Core Concept

Simulate distributed surface charges using discrete fictitious charges
Charges placed inside conductors or outside field region
Match boundary conditions on electrode surfaces

Charge Types

Point charges: General purpose
Line charges: Cylindrical symmetry
Ring charges: Axial symmetry
Combinations: Complex geometries

Methodology

Select charge types and positions
Choose contour points on electrode surfaces
Calculate potential coefficients
Solve for charge magnitudes
Validate and compute field distribution

CSM: Mathematical Formulation

Potential Calculation

Total potential at point \(P_i\) from \(n\) charges:

\[V_i = \sum_{j=1}^n P_{ij} q_j\]

where \(P_{ij}\) are potential coefficients

Example: Point Charge

For point charge \(q\) at distance \(r\):

\[V = \frac{q}{4\pi\epsilon r}, \quad P = \frac{1}{4\pi\epsilon r}\]

System of Equations

\[\begin{bmatrix} P_{11} & \cdots & P_{1n} \\ \vdots & \ddots & \vdots \\ P_{n1} & \cdots & P_{nn} \end{bmatrix} \begin{bmatrix} q_1 \\ \vdots \\ q_n \end{bmatrix} = \begin{bmatrix} V_1 \\ \vdots \\ V_n \end{bmatrix}\]

CSM: Field Calculation and Procedure

Electric Field Intensity

Vector sum of fields from individual charges:

\[E_x = \sum_{j=1}^n \frac{\partial P_{ij}}{\partial x} q_j = \sum_{j=1}^n (f_{ij})_x q_j\]

where \((f_{ij})_x\) are field intensity coefficients

Solution Procedure

Select charge types and locations strategically
Choose contour points (emphasize curves/corners)
Compute potential coefficient matrix \([P]\)
Solve linear system \([P][q] = [V]\)
Validate with additional checkpoints
Calculate electric field distribution

Critical Success Factor

Experience in charge selection significantly improves convergence

CSM: Advantages and Limitations

Advantages

Versatile: 2D/3D fields, with/without symmetry
Simple and computationally efficient
Accurate for curved surfaces
Fast compared to FDM/FEM
Effective for composite dielectrics

Limitations

Challenging for thin electrodes
Difficult for irregular boundaries
Experience-dependent charge selection
Sharp edges require special treatment

Enhancement

Surface Charge Simulation Method (SCSM) addresses thin electrode limitations
Adaptive charge placement algorithms
Hybrid approaches with other methods

Surface Charge Simulation Method (SCSM)

SCSM: Enhanced Surface Modeling

Key Innovation

Simulates equipotential surfaces with distributed surface charge density \(\sigma(x)\)
Charges placed directly on electrode contours
More physically accurate than CSM

Surface Charge Distribution

\[\sigma(x) = \sum_{k=0}^n S_k(x) \sigma_k\]

where \(S_k(x)\) are segment shape functions

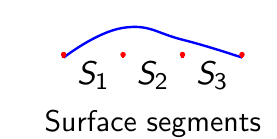
Advantage

Particularly effective for thin electrodes and sharp edges

SCSM: Mathematical Framework

Potential from Surface Charge

For surface charge density \(\sigma\) on contour \(C\):

\[V(P) = \frac{1}{4\pi\epsilon} \int_C \frac{\sigma(x')}{r(P,x')} dl'\]

Discretized Form

Dividing surface into \(n\) segments:

\[V_i = \sum_{j=1}^n P_{ij} \sigma_j \Delta l_j\]

System Solution

\[ [P][\sigma] = [V]\]

where \(\sigma\) contains surface charge density values

Field Calculation

\[\mathbf{E} = \sum_{j=1}^n \mathbf{f}_{ij} \sigma_j \Delta l_j\]

SCSM: Applications and Performance

Ideal Applications

Thin conductor strips
Sharp edges and corners
Complex curved boundaries
Multi-conductor systems
Transmission line analysis

Performance

Higher accuracy than CSM
Moderate computational cost
Good convergence properties

Comparison with CSM

Better: Surface representation
Better: Thin electrode handling
Similar: Computational efficiency
More complex: Implementation

Limitations

More complex setup than CSM
Requires careful segment sizing
Integration accuracy dependent

Electrolytic Tank Method

Electrolytic Tank: Analog Simulation

Physical Principle

Analog of electrostatic field problem
Exploits similarity between:
\[\begin{aligned} \mathbf{J} &= \sigma \mathbf{E} \quad \text{(current flow)} \\ \mathbf{D} &= \epsilon \mathbf{E} \quad \text{(electric field)} \end{aligned}\]
Both satisfy \(\nabla^2 V = 0\) in source-free regions

Setup Requirements

Conducting electrolyte (weak salt solution)
Scale model electrodes
Voltage source and measurement equipment
Probe for potential mapping

Electrolytic Tank: Measurement and Analysis

Measurement Process

Apply known voltage between model electrodes
Map equipotential lines using movable probe
Record voltage at regular grid points
Plot field lines perpendicular to equipotentials

Field Line Construction

Electric field lines are perpendicular to equipotentials
Direction: high to low potential
Density indicates field strength

Advantages

Visual field representation
2D and 3D capability
Physical insight
No computational requirements

Historical Importance

Pre-computer era standard
Educational demonstrations
Validation of numerical methods
Conceptual understanding

Comparative Analysis of Methods

Method Comparison: Accuracy and Efficiency

Comparative performance characteristics
Method	Accuracy	Speed	3D Capability	Complex Geometry	Implementation
FDM	Medium	Fast	Limited	Poor	Simple
FEM	High	Slow	Good	Excellent	Complex
CSM	High	Very Fast	Excellent	Good	Medium
SCSM	Very High	Fast	Good	Excellent	Medium
Tank	Medium	Manual	Limited	Good	Simple

Selection Guidelines

FDM: Simple 2D problems, educational purposes
FEM: Complex geometries, high accuracy requirements
CSM: General 3D problems, moderate complexity
SCSM: Thin electrodes, transmission lines
Tank: Visualization, concept demonstration

Computational Considerations

Memory Requirements

FDM: \(O(N^2)\) for 2D, \(O(N^3)\) for 3D
FEM: Depends on mesh density
CSM/SCSM: \(O(n^2)\) where \(n\) is number of charges
Modern computers handle most problems

Convergence

Grid refinement: FDM, FEM
Charge optimization: CSM, SCSM
Error estimation critical

Preprocessing

FDM: Grid generation
FEM: Mesh generation, quality
CSM: Charge placement strategy
SCSM: Surface discretization

Postprocessing

Field visualization
Maximum field identification
Corona inception prediction
Design optimization

Practical Applications and Case Studies

HV Equipment Analysis Applications

Power Transmission

Transmission lines: SCSM preferred
Substations: FEM for complex layouts
Insulators: CSM for 3D analysis
Corona studies: All methods applicable

Power Apparatus

Transformers: FEM for windings
Switchgear: CSM for electrodes
Cables: FDM for simple geometries
Capacitors: Method depends on design

Design Optimization

Electrode shaping: Minimize peak fields
Dielectric selection: Material properties
Spacing optimization: Cost vs performance
Corona mitigation: Surface treatment

Testing and Validation

Prototype validation: Compare with calculations
Standard compliance: IEEE, IEC requirements
Failure analysis: Field concentration points
Aging studies: Long-term field effects

Case Study: Transmission Line Design

Problem Statement

400 kV transmission line
Bundle conductor configuration
Corona inception voltage requirement
Environmental considerations (rain, pollution)

Analysis Approach

SCSM for surface field calculation
Multiple conductor bundle modeling
Weather effects incorporation
Optimization for minimum corona

Key Results

Optimized bundle spacing reduces maximum surface field by 25%, increasing corona inception voltage

Modern Developments and Future Trends

Advanced Numerical Techniques

Hybrid Methods

FEM-CSM coupling: Complex geometries with efficiency
Adaptive meshing: Automatic refinement
Multigrid techniques: Faster convergence
Parallel processing: HPC implementation

Enhanced Accuracy

Higher-order elements: Better field representation
Error estimation: Adaptive control
Mesh optimization: Optimal node placement
Singularity treatment: Sharp edge handling

Commercial Software

ANSYS Maxwell: General electromagnetics
COMSOL: Multiphysics coupling
Opera-3D: Specialized HV analysis
FEMM: Open-source 2D analysis

Emerging Technologies

Machine Learning: Pattern recognition in field analysis
AI optimization: Automated design
Cloud computing: Large-scale simulations
Real-time analysis: Embedded processing

Integration with Modern HV Systems

Smart Grid Applications

Real-time monitoring: Sensor integration with field models
Predictive maintenance: Field-based aging models
Dynamic rating: Environmental condition adaptation
Fault prediction: Stress concentration monitoring

Renewable Energy Integration

HVDC systems: New electrode configurations
Offshore wind: Marine environment effects
Solar farms: Large-scale grounding systems
Energy storage: Battery system field analysis

Environmental Considerations

Climate change: Extreme weather impact on fields
Pollution effects: Contamination modeling
Wildlife protection: Field exposure limits
EMF concerns: Public health considerations

Summary and Conclusions

Key Takeaways

Fundamental Principles

All methods solve Laplace’s equation: \(\nabla^2 V = 0\)
Choice depends on geometry, accuracy, and computational resources
Boundary conditions critical for all approaches

Method Selection Strategy

Educational/Simple: FDM or Electrolytic Tank
General Engineering: CSM for efficiency
High Accuracy/Complex: FEM
Transmission Lines: SCSM
Validation: Multiple method comparison

Professional Practice

Understanding multiple methods enables optimal tool selection for each application

Future Learning Path

Immediate Next Steps

Hands-on practice with each method
Software proficiency: Commercial tools
Validation studies: Compare methods
Case study analysis: Real applications

Advanced Topics

Time-varying fields
Nonlinear materials
Coupled physics problems
Optimization techniques

Practical Skills

Problem formulation: Boundary condition setup
Result interpretation: Physical meaning
Design optimization: Performance improvement
Standard compliance: Industry requirements

Career Development

Industry internships
Research projects
Professional societies (IEEE)
Continuing education

Next Lecture:
Breakdown in Gaseous Dielectrics

References for Further Reading

Kuffel, E., et al. "High Voltage Engineering Fundamentals"
Naidu, M.S. "High Voltage Engineering"
IEEE Standards for High Voltage Testing