Learning Objectives
By the end of this lecture, you will be able to:
-
Understand the fundamental mechanisms of gas breakdown
-
Analyze Townsend avalanche and secondary emission processes
-
Apply Paschen’s Law for breakdown voltage calculations
-
Distinguish between Townsend and streamer breakdown mechanisms
-
Evaluate corona discharge phenomena in non-uniform fields
-
Design considerations for gas-insulated systems
Introduction to Gas Breakdown
Introduction to Gas Breakdown
-
Growing demand for electrical energy increases power system size and complexity
-
Higher transmission voltages (e.g., 400 kV, 800 kV, 1200 kV planned globally) enhance power transfer and reduce losses
-
Conventional insulating materials for high-voltage systems are bulky and costly
-
New insulating materials are investigated to reduce cost and space
-
Insulation media classification: gases, liquids, solids, and composite systems
Key Statistics
Ultra High Voltage (UHV) lines operate at 800 kV AC and ±800 kV DC, with some reaching 1100 kV AC in China.
Role of Insulation in Power Systems
-
Live conductors supported by insulating materials
-
Air clearances: Prevent flashovers or short circuits in overhead lines
-
Insulating liquids: Reduce container size while ensuring insulation (transformers, capacitors)
-
Solid insulation: Provides mechanical support and electrical isolation
-
Study focuses on breakdown mechanisms of gases, liquids, and solids
Insulation Coordination
Proper coordination between different insulation levels ensures system reliability and cost optimization.
Mechanism of Breakdown of Gases
Properties of Gases
-
At normal temperature and pressure (NTP), gases are excellent insulators
-
Natural current conduction: \(\sim 10^{-10}\) to \(10^{-12} \, \mathrm{A/cm^2}\), due to:
-
Cosmic radiation (primary and secondary)
-
Natural radioactive substances
-
Photoionization from UV radiation
-
-
At high electric fields, charged particles gain energy, leading to ionization on impact
-
Critical field strength: Typically 30 kV/cm for air at STP
Did you know?
The natural background ionization creates about \(10^6\) to \(10^7\) ion pairs per cm³ per second in air.
Ionization by Electron Impact
-
Electrons gain kinetic energy from electric fields: \(KE = eVd\) where \(d\) is mean free path
-
Elastic collisions: Minimal energy loss (\(\sim 10^{-5}\) of electron energy), rapid energy buildup
-
Inelastic collisions: Energy transforms into potential energy, ionizing molecules
-
Primary process for gas breakdown under strong electric fields
Ionization Energy Requirements
-
Air: 15.6 eV, Nitrogen: 15.5 eV, Oxygen: 12.1 eV
-
Hydrogen: 15.4 eV, Helium: 24.5 eV, Argon: 15.7 eV
-
\(\mathrm{SF_6}\): 15.3 eV (but high electron attachment)
Photoionization
-
Occurs when photon energy exceeds ionization energy:
\[A + h\nu \rightarrow A^+ + e^- \quad \text{(if } h\nu > W_i\text{)}\] -
Secondary ionization process, crucial for streamer breakdown and corona discharges
-
Photoexcitation: absorbed energy raises atom to higher energy level if below ionization threshold
-
Photon sources: Recombination radiation, excited atom de-excitation
Important Note
Photoionization provides the "seed" electrons necessary for streamer propagation at light speed, making it faster than electron drift.
Ionization by Metastables
-
Metastable states: Long-lived excited electronic states (microseconds to seconds)
-
Metastables have high potential energy, can ionize neutral particles:
\[A + B^{\mathrm{m}} \rightarrow A^+ + B + e^-\] -
Responsible for long time lags in some gases (particularly noble gases)
-
Lifetime examples: He metastables: \(\sim 10^{-4}\) s, Ne metastables: \(\sim 10^{-2}\) s
Penning Mixtures
When one gas has metastable energy > ionization energy of another gas, enhanced breakdown occurs (Penning effect).
Thermal Ionization
-
Involves molecular collisions, radiation, and electron collisions at high temperatures
-
High-temperature gas molecules gain kinetic energy, ionizing neutral particles
-
Electrons and high-velocity molecules release more electrons
-
Recombination balances ionization at thermodynamic equilibrium
Temperature Requirements
-
Significant thermal ionization: \(\mathrm{T} > 2000 ~\mathrm{K}\) for most gases
-
Complete ionization (plasma): \(\mathrm{T} > 10,000 ~\mathrm{K}\)
-
Arc temperatures: \(5,000-20,000 ~\mathrm{K}\)
Saha’s Equation for Ionization
-
Degree of ionization \(\beta\) derived by Saha:
\[\frac{\beta^2}{1 - \beta^2} = \frac{2.4 \times 10^{-4}}{p} T^{5/2} e^{-W_i / kT}\] -
\(p\): pressure (Torr), \(W_i\): ionization energy (eV), \(k\): Boltzmann constant, \(T\): temperature (K)
-
Significant ionization only above 1000 K
-
At \(\beta = 0.5\) (50% ionization): \(T \approx 0.75 W_i/k\) for \(p = 760\) Torr
Example Calculation
For air at 1 atm: 50% ionization occurs at approximately 9,000 K
Townsend’s First Ionization Coefficient
Experimental Setup for Townsend’s Study
-
Parallel plate capacitor with gas as insulating medium, plates separated by distance \(d\)
-
Without electric field: equilibrium between electron and ion generation due to natural decay processes
-
Applying high electric field disturbs equilibrium, initiating ionization avalanche
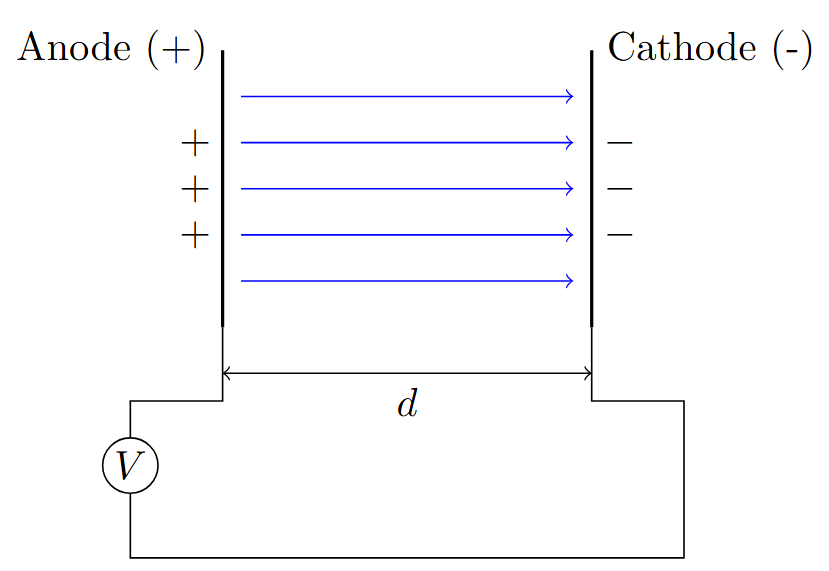
Key Parameters
Gap spacing: 0.1-10 cm, Pressure: 0.1-100 Torr, Voltage: 100-10,000 V
Current Variation with Voltage
-
Townsend’s observation of current vs. voltage characteristics:
-
Region I: Low voltage - current increases proportionally with voltage (Ohm’s law)
-
Region II: Intermediate voltage - current saturates at \(I_0\) (saturation current)
-
Region III: High voltage - current increases exponentially due to gas ionization
-
-
Higher \(V/d\) (electric field) accelerates electrons, increasing kinetic energy and electron production
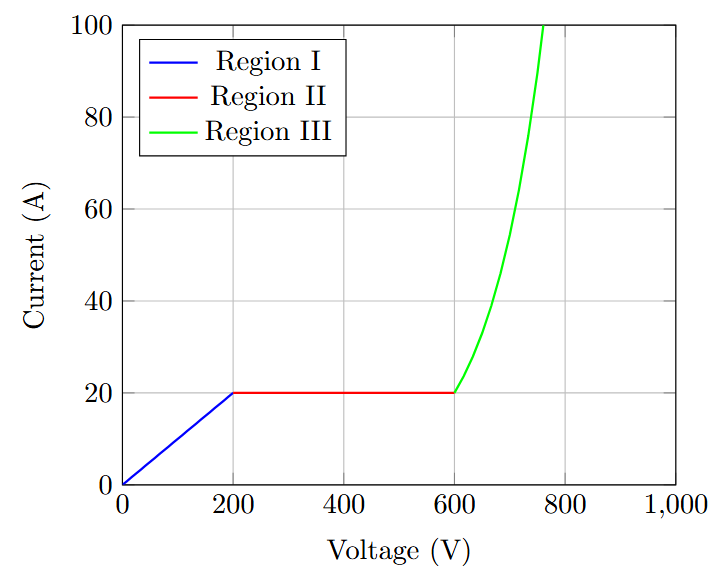
Definition of Townsend’s First Ionization Coefficient
-
Defined as \(\alpha\): number of ionizing collisions made by an electron per unit length in field direction
-
Physical meaning: probability of ionization per unit path length
-
Let \(n_0\) be electrons leaving cathode; at distance \(x\), number of electrons is \(n\)
-
In distance \(dx\), \(n\) electrons produce \(dn\) additional electrons:
\[dn = \alpha n \, dx\]
Units and Typical Values
-
Units: \(\mathrm{m}^{-1}\) or \(\mathrm{cm}^{-}\)
-
Air at STP: \(\alpha \approx 1-100~\mathrm{cm}^{-}\) (depends on E/p)
-
Often expressed as \(\alpha/p\) in units of \(\mathrm{cm}^{-} \cdot \mathrm{Torr}^{-1}\)
Derivation of Electron Avalanche
-
Differential equation for electron multiplication:
\[\frac{dn}{dx} = \alpha n \quad \Rightarrow \quad \frac{dn}{n} = \alpha \, dx\] -
Integrate from \(x=0\) (where \(n=n_0\)) to distance \(x\):
\[\int_{n_0}^{n} \frac{dn'}{n'} = \int_0^x \alpha \, dx' \quad \Rightarrow \quad \ln n - \ln n_0 = \alpha x\] -
Solution for electron avalanche:
\[n(x) = n_0 e^{\alpha x}\] -
At anode \((x=d)\): \(n = n_0 e^{\alpha d}\), hence current: \(I = I_0 e^{\alpha d}\)
-
Term \(e^{\alpha d}\) is the avalanche multiplication factor
\(\alpha/p\) vs \(E/p\) Relationship
-
Empirical relationship for most gases:
\[\frac{\alpha}{p} = A e^{-Bp/(E/p)} = A e^{-B p d / V}\] -
\(A\) and \(B\): gas-dependent constants
-
\(E/p\): reduced electric field ( \(V \cdot \mathrm{cm}^{-1}\cdot \mathrm{Torr}^{-1}\))
Constants for Common Gases
| Gas | A (\(\mathrm{cm}^{-1} \cdot \mathrm{Torr}^{-1}\)) | B (\(V \cdot \mathrm{cm}^{-1}\cdot \mathrm{Torr}^{-1}\)) |
|---|---|---|
| Air | 15 | 365 |
| N2 | 12 | 342 |
| O2 | 18 | 540 |
| H2 | 5 | 130 |
| He | 3 | 34 |
| Ar | 14 | 180 |
Cathode Processes - Secondary Effects
Role of Cathode in Gas Discharge
-
Cathode supplies electrons for initiation, sustenance, and completion of gas discharge
-
Electrons in metal are bound by electrostatic forces; energy required to release them is the work function \(W\) (typically 2-6 eV)
-
Electron emission mechanisms:
-
Thermionic emission (high temperature)
-
Field emission (high electric field)
-
Secondary emission (ion/photon bombardment)
-
Critical Role
Without cathode electron emission, self-sustained discharge cannot occur, regardless of gas multiplication.
Thermionic Emission
-
At high temperatures (\(T \geq \mathrm{1500}{K}\)), electrons gain thermal energy to overcome surface barrier
-
Richardson’s equation for saturation current density:
\[J_s = A_0 T^2 e^{-W / kT}, \quad A_0 = \frac{4\pi m_e k^2}{h^3} = 120 \times 10^4 \, \mathrm{A·m^{-2}·K^{-2}}\] -
Practical value: \(A \approx 60 \times 10^4 \, \mathrm{A·m^{-2}·K^{-2}}\) due to surface imperfections
-
Low work function metals preferred (tungsten: 4.5 eV, barium oxide: 1.0 eV)
Example
For tungsten at 2500 K: \(J_s \approx 1000~\mathrm{A/m^2}\)
Field Emission (Schottky Effect)
-
Strong electric field reduces effective work function:
\[W' = W - \sqrt{\frac{e^3 E}{4\pi\epsilon_0}} \approx W - 3.79 \times 10^{-5} \sqrt{E} \text{ eV (E in V/cm)}\] -
Modified Richardson equation:
\[J_s = A T^2 e^{-W' / kT} = A T^2 e^{-(W - 3.79 \times 10^{-5} \sqrt{E}) / kT}\] -
At very high fields (\(E > 10^7 \, \mathrm{V/cm}\)), quantum tunneling dominates
-
Fowler-Nordheim equation for field emission:
\[J = 1.54 \times 10^{-6} \frac{E^2}{\phi} \exp\left(-6.83 \times 10^7 \frac{\phi^{3/2}}{E}\right)\]
Secondary Emission by Ion Bombardment
-
Secondary emission: Positive ions with sufficient energy strike cathode, releasing electrons
-
Energy condition: \(W_k + W_p \geq 2W\) where:
-
\(W_k\): kinetic energy of ion
-
\(W_p\): potential energy of ion
-
\(W\): work function of cathode
-
-
One electron neutralizes the ion, another is emitted
-
Key mechanism in Townsend discharge
Secondary Emission Coefficient
Depends on: ion type, ion energy, cathode material, surface conditions
-
Clean metals: 0.01-0.3 electrons/ion
-
Oxidized surfaces: up to 0.5 electrons/ion
Photoemission and Metastable Bombardment
-
Photoemission: UV photons with \(h\nu > W\) release electrons from cathode
\[h\nu + \text{cathode} \rightarrow e^- + \text{cathode}^+\] -
Quantum efficiency: typically 0.01-0.1 electrons/photon for metals
-
Metastable bombardment: Excited atoms transfer energy to cathode
\[A^m + \text{cathode} \rightarrow A + e^- + \text{cathode}^+\] -
Important in noble gas discharges due to long metastable lifetimes
Combined Effect
In practice, all emission mechanisms contribute simultaneously to the total secondary coefficient \(\gamma\).
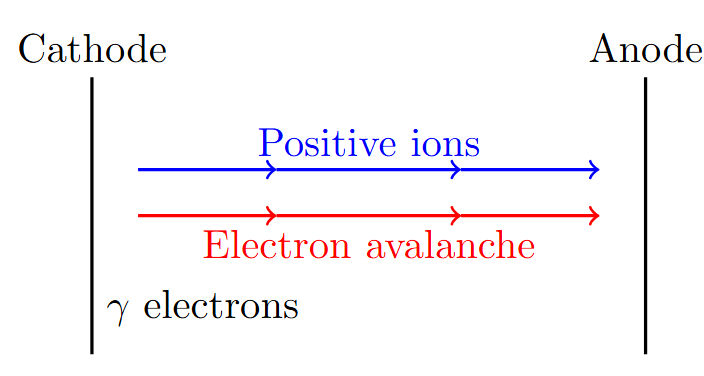
Townsend’s Second Ionization Coefficient
Need for Second Ionization Coefficient
-
First coefficient equation: \(I = I_0 e^{\alpha d}\) predicted slower current growth
-
Townsend observed current increases faster than predicted
-
Additional ionization sources identified:
-
Positive ions bombarding cathode
-
Photons causing photoemission
-
Metastable atoms at cathode
-
Volume recombination radiation
-
-
Need for secondary ionization coefficient \(\gamma\)
Defining Townsend’s Second Ionization Coefficient
-
\(\gamma\): Number of secondary electrons released from cathode per incident positive ion
-
Physical processes contributing to \(\gamma\):
-
Ion impact: \(\gamma_i\) (dominant at low pressures)
-
Photon impact: \(\gamma_{ph}\) (important in streamer formation)
-
Metastable impact: \(\gamma_m\) (significant in noble gases)
-
-
Total: \(\gamma = \gamma_i + \gamma_{ph} + \gamma_m\)
-
Typical values: \(\gamma = 10^{-4}\) to \(10^{-1}\) for most gas-cathode combinations
Measurement Methods
-
Steady-state current measurement
-
Pulsed discharge analysis
-
Photomultiplier detection of photons
Derivation of Current with Secondary Effects
-
Electron balance at cathode:
-
Primary electrons: \(n_0\) (from external sources)
-
Secondary electrons: \(n_+\) (from positive ion bombardment)
-
-
Electrons reaching anode: \(n = (n_0 + n_+) e^{\alpha d}\)
-
Positive ions produced in gap: \(n - (n_0 + n_+) = (n_0 + n_+)(e^{\alpha d} - 1)\)
-
Each positive ion releases \(\gamma\) electrons:
\[n_+ = \gamma (n_0 + n_+)(e^{\alpha d} - 1)\]
Key Assumption
All positive ions reach the cathode (valid for uniform fields and moderate pressures).
Final Current Expression with Secondary Effects
-
Solving for \(n_+\):
\[n_+ = \frac{\gamma n_0 (e^{\alpha d} - 1)}{1 - \gamma (e^{\alpha d} - 1)}\] -
Total electrons at anode:
\[n = n_0 \frac{e^{\alpha d}}{1 - \gamma (e^{\alpha d} - 1)}\] -
Final current expression:
\[I = I_0 \frac{e^{\alpha d}}{1 - \gamma (e^{\alpha d} - 1)}\]
Limiting Cases
-
\(\gamma \to 0\): \(I = I_0 e^{\alpha d}\) (first Townsend coefficient only)
-
\(\gamma (e^{\alpha d} - 1) \to 1\): \(I \to \infty\) (breakdown condition)
Factors Influencing \(\gamma\)
-
Cathode material: Lower work function \(W\) increases emission
-
Clean tungsten: \(\gamma \sim 10^{-3}\)
-
Oxidized surfaces: \(\gamma \sim 10^{-2}\)
-
Alkali metals: \(\gamma \sim 10^{-1}\)
-
-
Gas type: Affects ion energy and photon production
-
Pressure: Influences ion energy distribution
-
\(E/p\) ratio: Higher fields produce more energetic ions and photons
-
Surface conditions: Contamination, roughness, temperature
Practical Range
For engineering calculations: \(\gamma = 10^{-4}\) to \(10^{-2}\) for most practical conditions.
Townsend Breakdown Mechanism
Townsend Breakdown Criterion
-
Current with secondary effects:
\[I = I_0 \frac{e^{\alpha d}}{1 - \gamma (e^{\alpha d} - 1)}\] -
Current becomes infinite (breakdown) when denominator equals zero:
\[1 - \gamma (e^{\alpha d} - 1) = 0\] -
Townsend criterion for breakdown:
\[\gamma (e^{\alpha d} - 1) = 1 \quad \text{or} \quad \gamma e^{\alpha d} = \gamma + 1\] -
For \(\gamma \ll 1\): \(\boxed{\gamma e^{\alpha d} = 1}\) (simplified form)
Physical Interpretation of Townsend Criterion
-
At \(\gamma e^{\alpha d} = 1\): Self-sustaining condition reached
-
Each primary electron creates \((e^{\alpha d} - 1)\) positive ions in the gap
-
These ions produce \(\gamma(e^{\alpha d} - 1) = 1\) secondary electron at cathode
-
This electron creates another avalanche → continuous process
-
Result: Discharge continues even if initial source \(I_0\) is removed
Derivation of Paschen’s Law
-
From Townsend criterion: \(\gamma e^{\alpha d} = 1\)
-
Taking natural logarithm: \(\ln \gamma + \alpha d = 0\)
-
Substituting \(\alpha/p = A e^{-Bp/(E/p)}\):
\[\ln \gamma + A p d e^{-Bp d / V} = 0\] -
Rearranging: \(A p d e^{-Bp d / V} = -\ln \gamma\)
-
Let \(K = -\ln \gamma\) (positive constant), then:
\[A p d e^{-Bp d / V} = K\]
Key Insight
The breakdown voltage depends only on the product \(pd\) (pressure × gap distance), not on \(p\) and \(d\) individually.
Paschen’s Law - Final Form
-
From \(A p d e^{-Bp d / V} = K\), solving for \(V\):
\[e^{-Bp d / V} = \frac{K}{A p d}\] -
Taking natural logarithm:
\[-\frac{B p d}{V} = \ln\left(\frac{K}{A p d}\right) = \ln K - \ln A - \ln(p d)\] -
Paschen’s Law:
\[\boxed{V_b = \frac{B p d}{\ln(A p d) - \ln K} = \frac{B p d}{\ln\left(\frac{A p d}{K}\right)}}\]
Standard Form
Often written as: \(V_b = \frac{C(pd)}{\ln(pd) + D}\) where \(C\) and \(D\) are gas-dependent constants.
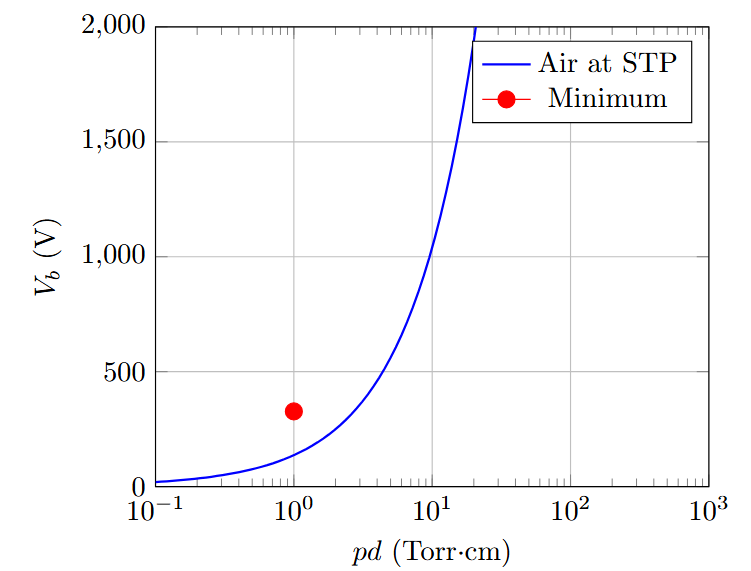
Paschen Curve Characteristics
-
Paschen curve shows \(V_b\) vs \(pd\) relationship
-
Key features:
-
Minimum breakdown voltage at optimal \(pd\)
-
Left branch: low pressure, long mean free path
-
Right branch: high pressure, short mean free path
-
-
Minimum occurs when: \(\frac{d}{d(pd)}[V_b] = 0\)
Paschen’s Law - Practical Applications
-
Minimum breakdown voltage for air: \(\sim 327\) V at \(pd = 1\) Torr·cm
-
Applications:
-
Design of gas-insulated equipment
-
Vacuum system breakdown prediction
-
High-altitude equipment insulation
-
Gas discharge tube design
-
-
Deviations from Paschen’s Law:
-
Very low pressures (mean free path > gap)
-
Very high pressures (attachment effects)
-
Non-uniform fields
-
Electrode surface effects
-
Design Example
For 1 mm gap in air at atmospheric pressure: \(pd = 760 \times 0.1 = 76\) Torr·cm, \(V_b \approx 3.2\) kV
Streamer Breakdown Mechanism
Limitations of Townsend Mechanism
-
Townsend theory assumes uniform field and steady-state conditions
-
Observed discrepancies:
-
Faster breakdown than predicted electron drift time
-
Lower breakdown voltages in non-uniform fields
-
Independence of breakdown time on gap distance
-
Luminous channels (streamers) observed
-
-
Typical conditions where Townsend fails:
-
\(pd > 1000\) Torr·cm
-
Non-uniform electric fields
-
Large gap distances (\(d > 1\) cm at atmospheric pressure)
-
Key Observation
Breakdown occurs in microseconds while electron drift takes milliseconds!
Streamer Formation Mechanism
-
Initial phase: Townsend avalanche creates space charge
-
Critical avalanche size: \(\sim 10^8\) electrons (Raether criterion)
-
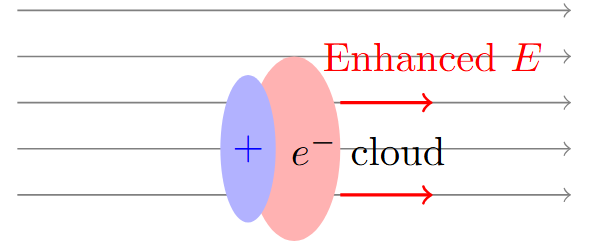
Space charge effects: Distort electric field
-
Enhanced field at avalanche head
-
Reduced field at avalanche tail
-
-
Streamer initiation: When space charge field comparable to applied field
-
Photoionization: Provides seed electrons ahead of avalanche
Raether Criterion
-
Critical condition for streamer formation:
\[\boxed{\alpha d \geq 18-20}\] -
At this point, avalanche contains \(\sim 10^8\) electrons
-
Space charge field becomes significant compared to applied field
-
Physical reasoning:
-
Electron cloud radius: \(\sim 10^{-4}\) m
-
Space charge field: \(E_{sc} \sim 10^6\) V/m
-
Comparable to applied breakdown fields
-
Example
For air at STP with \(\alpha = 100~\mathrm{m}^{-1}\): Critical gap \(d = 0.2\) m (20 cm)
Streamer Propagation
-
Positive streamer: Propagates toward cathode
-
High field at streamer tip ionizes gas
-
Electrons drift toward anode, leaving positive channel
-
Propagation velocity: \(\sim 10^7\) m/s
-
-
Negative streamer: Propagates toward anode (less common)
-
Photoionization role: Creates seed electrons ahead of streamer tip
-
Channel conductivity: Partially ionized, conductive path
Streamer vs Townsend
-
Townsend: Uniform ionization, electron drift limited
-
Streamer: Localized channels, light-speed propagation
Streamer-to-Arc Transition
-
Leader formation: Streamer channel heats up, becomes highly conductive
-
Return stroke: High current flows through leader channel
-
Arc formation: Thermal ionization sustains discharge
-
Current levels:
-
Streamer: \(\mu\)A to mA
-
Leader: mA to A
-
Arc: A to kA
-
Lightning Analogy
Lightning follows streamer-leader-return stroke sequence, with breakdown voltages of millions of volts!
Corona Discharge
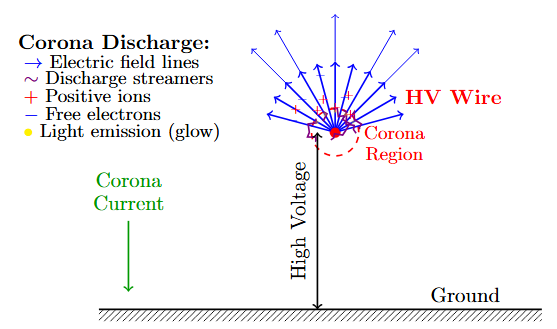
Corona Discharge in Non-Uniform Fields
-
Occurs in highly non-uniform electric fields
-
Common geometries:
-
Wire-to-plane (transmission lines)
-
Point-to-plane (lightning rods)
-
Wire-to-cylinder (coaxial cables)
-
-
Characteristics:
-
Localized ionization near high-field electrode
-
Self-limiting current due to space charge
-
Continuous discharge below breakdown voltage
-
Visible glow, audible noise, ozone production
-
Peek’s Formula for Corona Inception
-
For wire-to-plane geometry, corona inception field:
\[E_0 = E_{0,air} \left(1 + \frac{k}{\sqrt{r}}\right)\] -
Where:
-
\(E_{0,air} = 30\) kV/cm (critical field for air at STP)
-
\(k = 0.03\) cm\(^{1/2}\) (surface roughness factor)
-
\(r\): wire radius (cm)
-
-
Corona inception voltage:
\[V_c = E_0 r \ln\left(\frac{D}{r}\right)\] -
\(D\): distance to ground plane
Example
For 1 cm radius wire, 10 m height: \(V_c \approx 300\) kV
Types of Corona
-
Positive corona: Wire at positive potential
-
Streamer formation from wire surface
-
Pulsed, irregular discharge
-
Higher inception voltage
-
Greater power loss and radio interference
-
-
Negative corona: Wire at negative potential
-
Glow discharge near wire
-
Steady, uniform discharge
-
Lower inception voltage
-
Less radio interference
-
AC Corona
Alternates between positive and negative phases, with different characteristics in each half-cycle.
Corona Effects and Mitigation
-
Detrimental effects:
-
Power loss (especially in wet conditions)
-
Radio and TV interference
-
Audible noise
-
Ozone and NOx production
-
Conductor surface erosion
-
-
Mitigation strategies:
-
Larger conductor radius (bundled conductors)
-
Higher conductor height
-
Corona rings on insulators
-
Smooth conductor surfaces
-
Design Criterion
Transmission lines designed to operate below corona inception voltage under normal conditions.
Practical Applications and Design Considerations
Gas-Insulated Systems
-
Sulfur hexafluoride (\(SF_6\)): Superior insulating gas
-
Breakdown strength: 2-3 times air at same pressure
-
High electronegativity (electron attachment)
-
Chemically inert, non-toxic at normal concentrations
-
Self-healing after breakdown
-
-
Applications:
-
Gas-insulated switchgear (GIS)
-
Gas-insulated transmission lines (GIL)
-
High-voltage circuit breakers
-
Transformers (as alternative to oil)
-
Environmental Concerns
\(SF_6\) is a potent greenhouse gas (GWP = 22,800). Research focuses on alternatives like fluoronitriles.
Design Guidelines for Gas Insulation
-
Field uniformity: Avoid sharp edges and points
-
Surface finish: Smooth, clean surfaces essential
-
Particle control: Metallic particles drastically reduce breakdown strength
-
Pressure optimization: Balance between insulation and cost
-
Temperature effects: Account for gas density variations
-
Moisture control: Water vapor reduces breakdown strength
Typical Design Values
-
Safety factor: 1.5-2.0 for steady-state voltage
-
Impulse safety factor: 1.3-1.5
-
Particle-free gas essential for reliable operation
Vacuum Insulation
-
Principles: Eliminate gas molecules to prevent avalanche
-
Pressure requirements: \(< 10^{-4}\) Torr for effective insulation
-
Breakdown mechanisms in vacuum:
-
Field emission from cathode (primary)
-
Microdischarges from surface impurities
-
Electrode vapor formation
-
-
Applications: Vacuum circuit breakers, vacuum capacitors, electron tubes
Advantages and Disadvantages
Advantages: No gas handling, environmental friendly, compact design
Disadvantages: Vacuum maintenance, field emission sensitivity
Summary and Conclusions
Summary
-
Gas breakdown mechanisms:
-
Townsend avalanche for uniform fields and low \(pd\)
-
Streamer mechanism for non-uniform fields and high \(pd\)
-
Corona discharge in highly non-uniform fields
-
-
Key parameters:
-
First ionization coefficient \(\alpha\)
-
Secondary emission coefficient \(\gamma\)
-
Townsend criterion: \(\gamma e^{\alpha d} = 1\)
-
Paschen’s Law: \(V_b = f(pd)\)
-
-
Engineering applications: GIS, vacuum systems, transmission lines
Key Takeaways
Design Principles
-
Uniform electric fields preferred for predictable breakdown
-
Surface condition critical for consistent performance
-
Pressure-distance product determines breakdown voltage
-
Environmental factors (temperature, humidity) affect performance
Future Trends
-
Alternative gases to \(SF_6\) for environmental sustainability
-
Vacuum technology for compact switchgear
-
Solid-gas composite insulation systems
-
Smart monitoring of insulation condition
References
E. Kuffel, W.S. Zaengl, J. Kuffel, High Voltage Engineering Fundamentals, 2nd Edition, Newnes, 2000.
M.S. Naidu, V. Kamaraju, High Voltage Engineering, 5th Edition, McGraw-Hill, 2013.
C.L. Wadhwa, High Voltage Engineering, 3rd Edition, New Age International, 2007.
H.M. Ryan, High Voltage Engineering and Testing, 3rd Edition, IET, 2013.