\(\begin{bmatrix} -2 & -2 & 2 \end{bmatrix}^T\)
\(\begin{bmatrix} 3 & 0 & -1 \end{bmatrix}^T\)
\(\begin{bmatrix} 3 & 2 & 1 \end{bmatrix}^T\)
\(\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}^T\)
The equation of a plane in matrix form is \(\mathbf{n}^T \mathbf{x} = d\), where \(\mathbf{n}\) is the normal vector. The given equation is \(\mathbf{w}^T\mathbf{x} = 1\). Comparing the equations, the normal vector \(\mathbf{n}\) is \(\mathbf{w}\). \[\mathbf{n} = \mathbf{w} = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}^T\]
The correct option is D. \(\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}^T\).

\(\begin{bmatrix} \frac{4}{5} & \frac{3}{5} \\ -\frac{3}{5} & \frac{4}{5} \end{bmatrix}\)
\(\begin{bmatrix} \frac{4}{5} & -\frac{3}{5} \\ \frac{3}{5} & \frac{4}{5} \end{bmatrix}\)
\(\begin{bmatrix} \frac{4}{5} & \frac{3}{5} \\ \frac{3}{5} & \frac{4}{5} \end{bmatrix}\)
\(\begin{bmatrix} \frac{3}{5} & -\frac{4}{5} \\ \frac{4}{5} & -\frac{3}{5} \end{bmatrix}\)
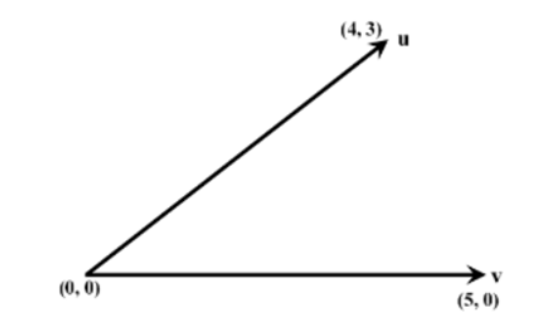
From the figure, the vectors are \(\mathbf{u} = \begin{bmatrix} 4 \\ 3 \end{bmatrix}\) and \(\mathbf{v} = \begin{bmatrix} 5 \\ 0 \end{bmatrix}\). We must satisfy \(\mathbf{A}\mathbf{u} = \mathbf{v}\).
Check Option A: \[\mathbf{A}\mathbf{u} = \begin{bmatrix} \frac{4}{5} & \frac{3}{5} \\ -\frac{3}{5} & \frac{4}{5} \end{bmatrix} \begin{bmatrix} 4 \\ 3 \end{bmatrix} = \begin{bmatrix} \frac{16}{5} + \frac{9}{5} \\ -\frac{12}{5} + \frac{12}{5} \end{bmatrix} = \begin{bmatrix} \frac{25}{5} \\ 0 \end{bmatrix} = \begin{bmatrix} 5 \\ 0 \end{bmatrix} = \mathbf{v}\]
The correct option is A. \(\begin{bmatrix} \frac{4}{5} & \frac{3}{5} \\ -\frac{3}{5} & \frac{4}{5} \end{bmatrix}\).
The \(\sigma_o\) is estimated by randomly drawing out \(10,000\) numbers of samples \((x_n)\). The estimates \(\hat{\sigma}_1^2, \hat{\sigma}_2^2\) are computed in the following two ways. \[\hat{\sigma}_1^2 = \frac{1}{10000} \sum_{n=1}^{10000} x_n^2, \quad \hat{\sigma}_2^2 = \frac{1}{9999} \sum_{n=1}^{10000} x_n^2\]
Which of the following statements is true?
\(E(\hat{\sigma}_2^2) = \sigma_o^2\)
\(E(\hat{\sigma}_2) = \sigma_o\)
\(E(\hat{\sigma}_1^2) = \sigma_o^2\)
\(E(\hat{\sigma}_1) = E(\hat{\sigma}_2)\)
The population mean \(\mu=0\) and variance \(\sigma^2 = \sigma_o^2\). Since \(\mu=0\), \(E[X^2] = \sigma^2\). The expected value of the first estimator \(\hat{\sigma}_1^2\) (with \(N=10000\)) is: \[E(\hat{\sigma}_1^2) = E\left[ \frac{1}{N} \sum_{n=1}^{N} x_n^2 \right] = \frac{1}{N} \sum_{n=1}^{N} E[x_n^2] = \frac{1}{N} (N \sigma_o^2) = \sigma_o^2\] Since \(E(\hat{\sigma}_1^2) = \sigma_o^2\), \(\hat{\sigma}_1^2\) is an **unbiased estimator** of the population variance \(\sigma_o^2\) when the mean is known to be zero.
The correct option is C. \(E(\hat{\sigma}_1^2) = \sigma_o^2\).
(Numerical Answer Type)
We use Euler’s method with a step size \(h = 1 - 0 = 1\). Euler’s Method: \(y_{n+1} = y_n + h f(t_n, y_n)\). Given \(t_0 = 0\), \(y_0 = 0\), \(h=1\), and \(f(t, y) = \frac{e^{-0.01t}}{2+0.01t}\).
Step 1 (at \(t_1=1\)): \[y_1 = y_0 + 1 \cdot f(0, 0) = 0 + 1 \cdot \left[ \frac{e^{-0.01 \cdot 0}}{2+0.01 \cdot 0} \right] = 1 \cdot \frac{e^{0}}{2} = \frac{1}{2} = 0.5\]
The value of \(y(t)\) at \(t=1\) is \(0.5\). Rounding off to 2 decimal places, the answer is \(\mathbf{0.50}\).
(Numerical Answer Type)
This is a Geometric Distribution problem. Let \(P\) be the probability of a Head (success). 1. Find \(P\): The expected number of trials \(E(X)\) is \(\frac{1}{P}\). \[4 = \frac{1}{P} \implies P = \frac{1}{4}\] The probability of a Tail (failure) is \(q = 1 - P = 1 - \frac{1}{4} = \frac{3}{4}\).
2. Find \(P(X=2)\): The probability of the first Head occurring on the second trial is \(P(T \text{ then } H)\). \[P(X=2) = q \cdot P = \frac{3}{4} \times \frac{1}{4} = \frac{3}{16}\]
3. Convert and round: \[\frac{3}{16} = 0.1875\] Rounding off to 3 decimal places, the answer is \(\mathbf{0.188}\).
(Numerical Answer Type)
The **maximum rate of change** of a scalar function \(f\) occurs in the direction of the gradient \(\nabla f\), and its magnitude is \(|\nabla f|\).
1. Calculate the Gradient (\(\nabla f\)): \[\nabla f = \frac{\partial f}{\partial x_1}\hat{i} + \frac{\partial f}{\partial x_2}\hat{j}\] \[\frac{\partial f}{\partial x_1} = 2x_1 + 0 + 3 + 0 + x_2 + 0 = 2x_1 + x_2 + 3\] \[\frac{\partial f}{\partial x_2} = 0 + 4x_2 + 0 + 3 + x_1 + 0 = x_1 + 4x_2 + 3\] \[\nabla f = (2x_1 + x_2 + 3)\hat{i} + (x_1 + 4x_2 + 3)\hat{j}\]
2. Evaluate the Gradient at \(P=(1, 1)\): \[\nabla f|_{(1, 1)} = (2(1) + 1 + 3)\hat{i} + (1 + 4(1) + 3)\hat{j}\] \[\nabla f|_{(1, 1)} = 6\hat{i} + 8\hat{j}\]
3. Calculate the Magnitude: \[|\nabla f|_{(1, 1)} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\]
Rounding off to the nearest integer, the answer is \(\mathbf{10}\).