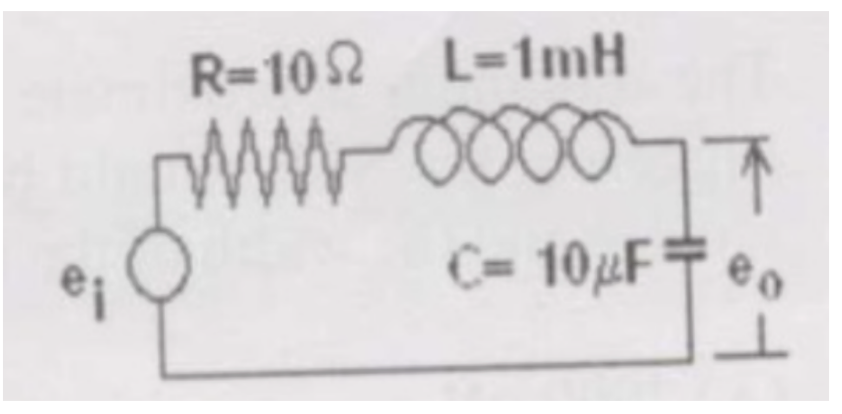
Consider the R-L-C circuit shown in figure:

If the above step response is to be observed on a non-storage CRO, then it would be best to have the \(e_i\) as a
Step function
Square wave of 50 Hz
Square wave of 300 Hz
Square wave of 2.0 KHz
Solution:
\[\omega_{n}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{1\times 10^{-3}\times 10\times 10^{-6}}}=10^{4}\,\text{rad/sec}\]
Settling time (\(t_{s}\)) = \(\frac{4}{\zeta\omega_{n}}\) = \(\frac{4}{10^{4}\times 0.5}\) = 0.8 msec.
For a square wave T/2 should be greater than \(t_{s}\):
For \(f_{1}=50\)Hz: \(\frac{T_{1}}{2}\) = \(\frac{1}{2\times 50}\) = 10ms > \(t_{s}\)
For \(f_{2}=300\)Hz: \(\frac{T_{2}}{2}\) = \(\frac{1}{2\times 300}\) = 1.67ms > \(t_{s}\)
For \(f_{3}=2\)kHz: \(\frac{T_{3}}{2}\) = \(\frac{1}{2\times 2000}\) = 0.25ms < \(t_{s}\)
Therefore, it would be best to have \(e_{i}\) as a square wave of 300Hz.
Correct answer: C
A function \(y(t)\) satisfies the following differential equation:
\[\frac{dy(t)}{dt} + y(t) = \delta(t)\]
where \(\delta(t)\) is the delta function. Assuming zero initial condition, and denoting the unit step function by \(u(t)\), \(y(t)\) can be of the form
\(e^t\)
\(e^{-t}\)
\(e^t u(t)\)
\(e^{-t} u(t)\)
Solution:
Taking Laplace Transform on both sides:
\[sY(s)+Y(s)=1\] \[Y(s)(s+1)=1\] \[\therefore Y(s)=\frac{1}{s+1}\]
Taking inverse Laplace transform:
\[y(t)=e^{-t}u(t)\]
Correct answer: D
The transfer function of a linear time invariant system is given as
\[G(s) = \frac{1}{s^2 + 3s + 2}\]
The steady state value of the output of the system for a unit impulse input applied at time instant \(t = 1\) will be
0
0.5
1
2
Solution:
\(r(t)=\) unit impulse applied at \(t=1=\delta(t-1)\)
\[R(s)=\mathcal{L}[r(t)]=e^{-s}\] \[G(s)=\frac{C(s)}{R(s)}=\frac{1}{s^{2}+3s+2}\] \[C(s)=R(s)G(s)=\frac{e^{-s}}{s^{2}+3s+2}\]
Steady state value of output, using final value theorem:
\[C_{ss}=\lim_{s\to 0}sC(s)=\lim_{s\to 0}\frac{se^{-s}}{s^{2}+3s+2}=0\]
Correct answer: A
The transfer functions of two compensators are given below:
\[C_1 = \frac{10(s+1)}{(s+10)}, \quad C_2 = \frac{s+10}{10(s+1)}\]
Which one of the following statements is correct?
\(C_1\) is a lead compensator and \(C_2\) is a lag compensator
\(C_1\) is a lag compensator and \(C_2\) is a lead compensator
Both \(C_1\) and \(C_2\) are lead compensators
Both \(C_1\) and \(C_2\) are lag compensators
Solution:
For \(C_1 = \frac{10(s+1)}{(s+10)}\):
Zero at \(s = -1\)
Pole at \(s = -10\)
As zero is closer to origin, zero dominates pole. Hence \(C_1\) is lead compensator.
For \(C_2 = \frac{s+10}{10(s+1)}\):
Zero at \(s = -10\)
Pole at \(s = -1\)
As pole is closer to origin, pole dominates zero. Hence \(C_2\) is lag compensator.
Correct answer: A
The asymptotic Bode magnitude plot of a minimum phase transfer function is shown in the figure:
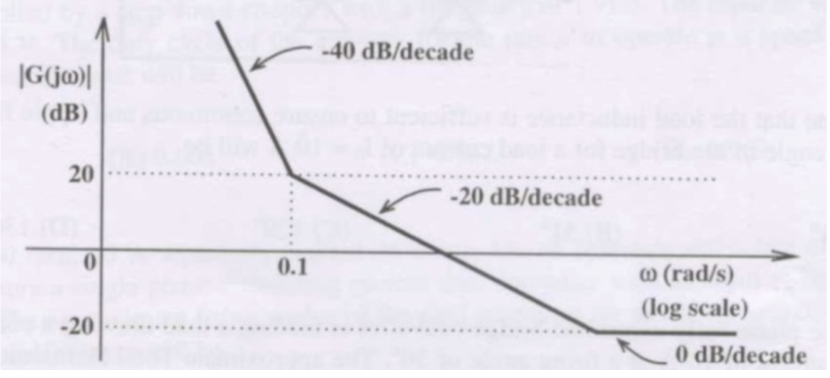
This transfer function has
Three poles and one zero
Two poles and one zero
Two poles and two zeros
One pole and two zeros
Solution:
Initial slope is -40 dB/decade, it means there are double pole at origin.
Slope changes from -40 dB/decade to -20 dB/decade. It means there is a zero.
Slope changes from -20 dB/decade to 0 dB/decade at some other frequency, means there is one more zero.
Therefore transfer function has two poles and two zeros.
Correct answer: C
Figure shows a feedback system where \(K > 0\)

The range of \(K\) for which the system is stable will be given by
\(0 < K < 30\)
\(0 < K < 39\)
\(0 < K < 390\)
\(K > 390\)
Solution:
\[G(s) = \frac{K}{s(s+3)(s+10)} \quad \text{and} \quad H(s) = 1\]
Characteristic equation:
\[1 + G(s)H(s) = 0\] \[1 + \frac{K}{s(s+3)(s+10)} = 0\] \[\Rightarrow s(s+3)(s+10) + K = 0\] \[\Rightarrow s^3 + 13s^2 + 30s + K = 0\]
Routh Array:
\[\begin{array}{c|cc} s^3 & 1 & 30 \\ s^2 & 13 & K \\ s^1 & \frac{13 \times 30 - K}{13} & 0 \\ s^0 & K & 0 \end{array}\]
According to Routh-Hurwitz criterion:
\(K > 0\)
\(\frac{13 \times 30 - K}{13} > 0 \Rightarrow 390 - K > 0 \Rightarrow K < 390\)
Therefore for system to be stable: \(0 < K < 390\)
Correct answer: C
The transfer function of a system is given as \(\frac{100}{s^2+20s+100}\). This system is
An over damped system
An under damped system
A critically damped system
An unstable system
Solution:
\[M(s)=\frac{100}{s^{2}+20s+100}\]
Comparing with standard form:
\[M(s)=\frac{\omega_{n}^{2}}{s^{2}+2\xi\omega_{n}s+\omega_{n}^{2}}\]
\[\omega_{n}^{2}=100\Rightarrow\omega_{n}=10\] \[2\xi\omega_{n}=20\Rightarrow 2\xi(10)=20\Rightarrow\xi=1\]
Since \(\xi=1\), the system is critically damped.
Correct answer: C
The state space equation of a system is described by
\[\dot{x} = Ax + Bu, \quad y = Cx\]
where \(x\) is state vector, \(u\) is input, \(y\) is output and
\[A = \begin{bmatrix} 0 & 1 \\ 0 & -2 \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \quad C = [1 \ 0]\]
The transfer function \(G(s)\) of this system will be
\(\frac{s}{(s+2)}\)
\(\frac{s+1}{(s+2)}\)
\(\frac{s}{(s-2)}\)
\(\frac{1}{s(s+2)}\)
Solution:
\[[sI-A] = \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} - \begin{bmatrix} 0 & 1 \\ 0 & -2 \end{bmatrix} = \begin{bmatrix} s & -1 \\ 0 & s+2 \end{bmatrix}\]
\[[sI-A]^{-1} = \frac{1}{s(s+2)} \begin{bmatrix} s+2 & 1 \\ 0 & s \end{bmatrix}\]
Transfer function:
\[G(s) = C[sI-A]^{-1}B + D\]
\[= \begin{bmatrix} 1 & 0 \end{bmatrix} \frac{1}{s(s+2)} \begin{bmatrix} s+2 & 1 \\ 0 & s \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix}\]
\[= \begin{bmatrix} 1 & 0 \end{bmatrix} \frac{1}{s(s+2)} \begin{bmatrix} 1 \\ s \end{bmatrix}\]
\[= \frac{1}{s(s+2)}\]
Correct answer: D