Detailed Notes on System Modeling & Feedback Control Systems for GATE EE Exam

Introduction

System Modeling and Feedback

Key Topics Covered

  • Mathematical modeling of physical systems

  • Transfer function representation

  • Block diagram reduction techniques

  • Signal flow graphs (Mason’s Gain Formula)

  • Feedback concepts and properties

  • System types and error constants

GATE EE Objective

Master the fundamentals of modeling and analyzing control systems with emphasis on problem-solving techniques for GATE EE examination.

Mathematical Modeling

Mathematical Modeling of Physical Systems

Basic Elements

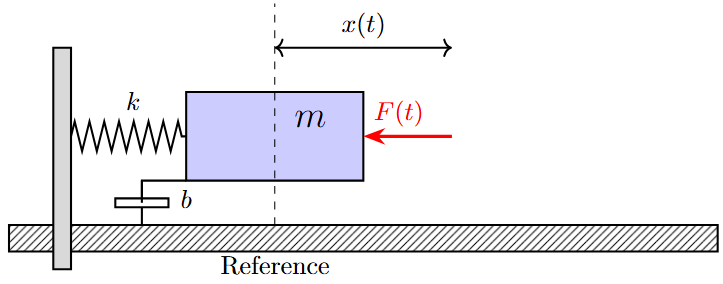
Mechanical Systems:

  • Mass (\(m\)): \(F = ma\)

  • Spring (\(k\)): \(F = kx\)

  • Damper (\(b\)): \(F = b\dot{x}\)

Electrical Systems:

  • Resistor (\(R\)): \(V = IR\)

  • Inductor (\(L\)): \(V = L\frac{dI}{dt}\)

  • Capacitor (\(C\)): \(I = C\frac{dV}{dt}\)

Example

Mass-Spring-Damper System:

\[m\ddot{x} + b\dot{x} + kx = F(t)\]
Taking Laplace transform:
\[ms^2X(s) + bsX(s) + kX(s) = F(s)\]
\[G(s) = \frac{X(s)}{F(s)} = \frac{1}{ms^2 + bs + k}\]

Mechanical System Diagram

Mechanical system representation
Mechanical system representation

Analogous Systems

Force-Voltage Analogy

Mechanical Electrical Relationship
Force \(F\) Voltage \(V\) Through variable
Velocity \(\dot{x}\) Current \(I\) Across variable
Mass \(m\) Inductance \(L\) \(F = m\ddot{x} \leftrightarrow V = L\frac{dI}{dt}\)
Damping \(b\) Resistance \(R\) \(F = b\dot{x} \leftrightarrow V = RI\)
Spring \(k\) \(\frac{1}{C}\) \(F = k\int \dot{x}dt \leftrightarrow V = \frac{1}{C}\int I dt\)

Important Note

Force-Current analogy is dual to Force-Voltage analogy. Choose the appropriate analogy based on the system configuration.

Transfer Function

Transfer Function Definition

The transfer function \(G(s)\) of a Linear Time-Invariant (LTI) system is defined as:

\[G(s) = \frac{Y(s)}{X(s)} = \frac{\mathcal{L}[\text{output}]}{\mathcal{L}[\text{input}]}\]
with zero initial conditions.

Key Properties

  • Valid only for LTI systems

  • Independent of input signal magnitude

  • Characteristic equation: \(1 + G(s)H(s) = 0\)

  • Poles: Roots of denominator polynomial

  • Zeros: Roots of numerator polynomial

  • System order = degree of denominator polynomial

Standard Transfer Functions

First-Order System

\[G(s) = \frac{K}{\tau s + 1}\]
where \(K\) is DC gain and \(\tau\) is time constant.

Second-Order System

\[G(s) = \frac{K\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2}\]
where \(\omega_n\) is natural frequency and \(\zeta\) is damping ratio.

GATE Tip

For GATE problems, quickly identify system type by denominator degree:

  • Type 0: No \(s\) in denominator

  • Type 1: One \(s\) in denominator

  • Type 2: Two \(s\) terms in denominator

Block Diagrams

Block Diagram Reduction Rules

Series Connection

control_series_connection

Parallel Connection

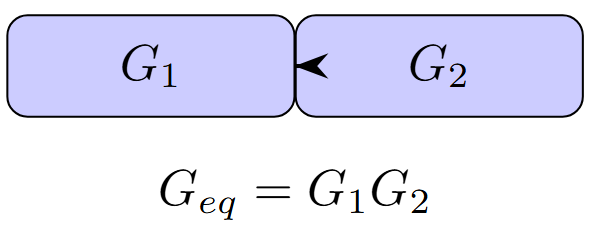
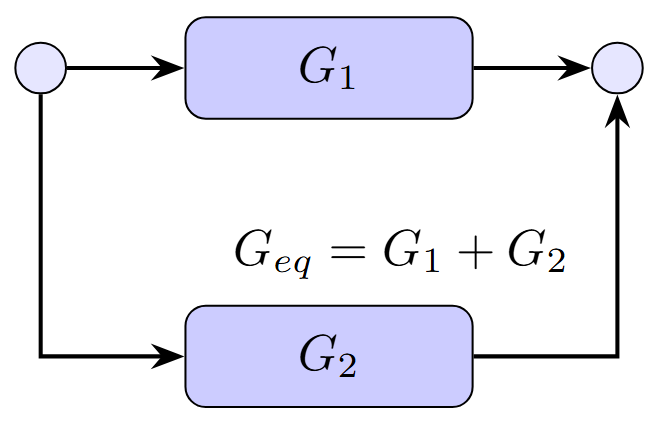
control_parallel_connection

Feedback Connection

control_feedback_connection

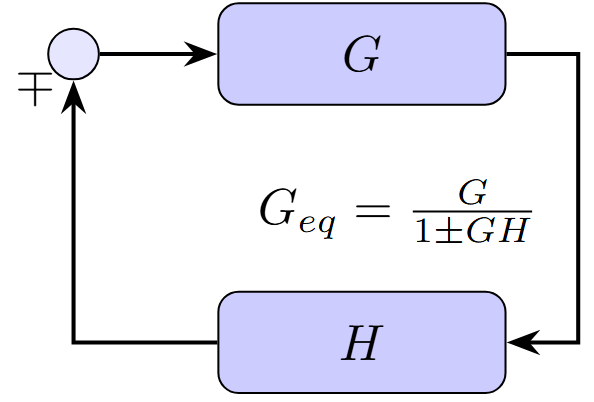
Sign Convention

  • Negative feedback: \(\frac{G}{1 + GH}\)

  • Positive feedback: \(\frac{G}{1 - GH}\)

Complex Block Diagram Example

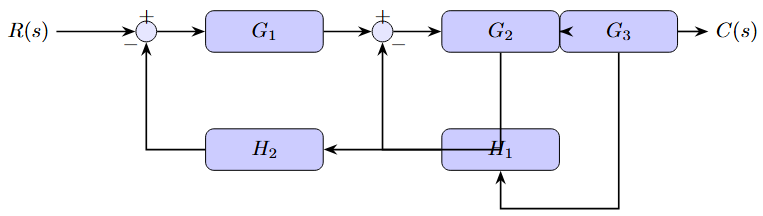
complex_example

Equivalent Transfer Function

\[\frac{C(s)}{R(s)} = \frac{G_1 G_2 G_3}{1 + G_1 G_2 H_2 + G_2 G_3 H_1 + G_1 G_2 G_3 H_1 H_2}\]

Signal Flow Graphs

Signal Flow Graph Terminology

Basic Terms

  • Node: Junction point representing a variable

  • Branch: Directed line segment with gain

  • Path: Sequence of connected branches

  • Loop: Closed path

  • Forward Path: Path from input to output

  • Non-touching loops: Loops with no common nodes

Example

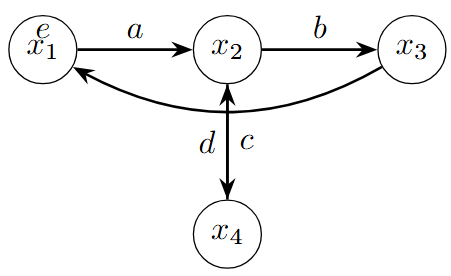
signal_flow

Mason’s Gain Formula

Formula

The overall transfer function is:

\[T = \frac{1}{\Delta} \sum_{k=1}^{N} P_k \Delta_k\]
where:

  • \(P_k\) = Gain of \(k^{th}\) forward path

  • \(\Delta\) = Graph determinant

  • \(\Delta_k\) = Cofactor for \(k^{th}\) path

Graph Determinant

\[\Delta = 1 - \sum L_i + \sum L_i L_j - \sum L_i L_j L_k + \cdots\]
where \(L_i\) are individual loop gains, \(L_i L_j\) are products of non-touching loop pairs, etc.

GATE Strategy

For complex systems, Mason’s formula is often faster than block diagram reduction.

Mason’s Formula Example

Consider the signal flow graph:

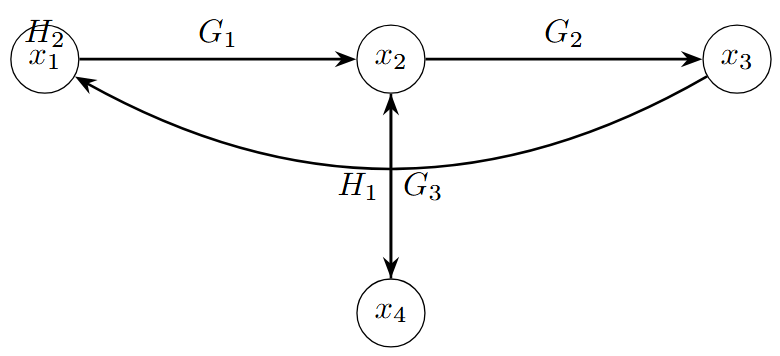
signal_flow1

Solution:

  • Forward path: \(P_1 = G_1 G_2\)

  • Loops: \(L_1 = G_3 H_1\), \(L_2 = G_1 G_2 H_2\)

  • \(\Delta = 1 - (G_3 H_1 + G_1 G_2 H_2)\)

  • \(\Delta_1 = 1 - G_3 H_1\) (removing \(L_2\) which touches the forward path)

  • \(T = \frac{G_1 G_2 (1 - G_3 H_1)}{1 - G_3 H_1 - G_1 G_2 H_2}\)

Feedback Concepts

Feedback System Analysis

Closed-Loop System

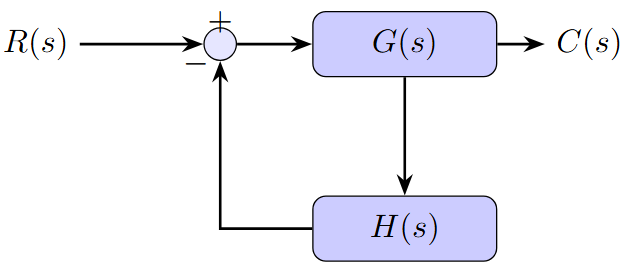
closed_system

Key Equations

  • Error: \(E(s) = R(s) - H(s)C(s)\)

  • Closed-loop TF: \(T(s) = \frac{G(s)}{1 + G(s)H(s)}\)

  • Error TF: \(\frac{E(s)}{R(s)} = \frac{1}{1 + G(s)H(s)}\)

Important Relations

  • Open-loop TF: \(G(s)H(s)\)

  • Characteristic equation: \(1 + G(s)H(s) = 0\)

  • For unity feedback: \(H(s) = 1\)

Advantages and Disadvantages of Feedback

Advantages

  • Reduced sensitivity to parameter variations

  • Improved stability and transient response

  • Reduced effect of noise and disturbances

  • Improved accuracy in steady-state

  • Bandwidth modification possible

Disadvantages

  • Reduced overall gain

  • Potential instability if poorly designed

  • Increased complexity and cost

  • May introduce noise through feedback path

Sensitivity Analysis

Sensitivity of closed-loop system to open-loop gain variations:

\[S_G^T = \frac{1}{1 + GH} \text{ vs. } S_G^G = 1 \text{ (open-loop)}\]
Feedback reduces sensitivity by factor \((1 + GH)\).

System Types

System Types and Error Constants

System Type Classification

Based on number of poles at origin in \(G(s)H(s)\):

\[G(s)H(s) = \frac{K(s + z_1)(s + z_2)\cdots}{s^N(s + p_1)(s + p_2)\cdots}\]
System is Type \(N\) (N = 0, 1, 2, ...).

Error Constants

  • Position Error Constant: \(K_p = \lim_{s \to 0} G(s)H(s)\)

  • Velocity Error Constant: \(K_v = \lim_{s \to 0} s \cdot G(s)H(s)\)

  • Acceleration Error Constant: \(K_a = \lim_{s \to 0} s^2 \cdot G(s)H(s)\)

Steady-State Errors

  • Step input: \(e_{ss} = \frac{1}{1 + K_p}\)

  • Ramp input: \(e_{ss} = \frac{1}{K_v}\)

  • Parabolic input: \(e_{ss} = \frac{1}{K_a}\)

Error Constants Table

Steady-State Error Constants
System Type \(K_p\) \(K_v\) \(K_a\)
Type 0 \(K\) \(0\) \(0\)
Type 1 \(\infty\) \(K\) \(0\)
Type 2 \(\infty\) \(\infty\) \(K\)
Steady-State Errors
Input Type 0 Type 1 Type 2
Step \(\frac{1}{1+K_p}\) \(0\) \(0\)
Ramp \(\infty\) \(\frac{1}{K_v}\) \(0\)
Parabolic \(\infty\) \(\infty\) \(\frac{1}{K_a}\)

GATE Practice

GATE Practice Questions - 1

Example

The transfer function of a system is \(G(s) = \frac{10}{s^2 + 3s + 2}\). The DC gain is:

  1. 0

  2. 5

  3. 10

  4. \(\frac{10}{2} = 5\)

Solution

DC gain is found by substituting \(s = 0\):

\[G(0) = \frac{10}{0^2 + 0 + 2} = \frac{10}{2} = 5\]
Answer: B

GATE Practice Questions - 2

Example

For a unity feedback system with \(G(s) = \frac{4}{s(s+2)}\), the closed-loop transfer function is:

  1. \(\frac{4}{s^2 + 2s + 4}\)

  2. \(\frac{4}{s^2 + 2s}\)

  3. \(\frac{2}{s^2 + 2s + 4}\)

  4. \(\frac{4}{s + 2}\)

Solution

For unity feedback: \(H(s) = 1\)

\[T(s) = \frac{G(s)}{1 + G(s)} = \frac{\frac{4}{s(s+2)}}{1 + \frac{4}{s(s+2)}} = \frac{4}{s(s+2) + 4} = \frac{4}{s^2 + 2s + 4}\]
Answer: A

GATE Practice Questions - 3

Example

A Type 1 system has \(G(s)H(s) = \frac{20}{s(s+4)}\). The velocity error constant \(K_v\) is:

  1. 4

  2. 5

  3. 20

  4. \(\infty\)

Solution

For Type 1 system:

\[K_v = \lim_{s \to 0} s \cdot G(s)H(s) = \lim_{s \to 0} s \cdot \frac{20}{s(s+4)} = \lim_{s \to 0} \frac{20}{s+4} = \frac{20}{4} = 5\]
Answer: B

GATE Practice Questions - 4

The Mason’s gain formula for the system shown requires calculation of:

  1. Forward paths and loops only

  2. Forward paths, loops, and their cofactors

  3. Only the characteristic polynomial

  4. Transfer function directly

Solution

Mason’s gain formula requires:

  • All forward paths and their gains

  • All loops and their gains

  • Cofactors for each forward path

  • Graph determinant calculation

Answer: B

GATE Practice Questions - 5

Example

For the block diagram shown, if \(G_1 = 2\), \(G_2 = 3\), and \(H = 0.5\), the overall transfer function is:

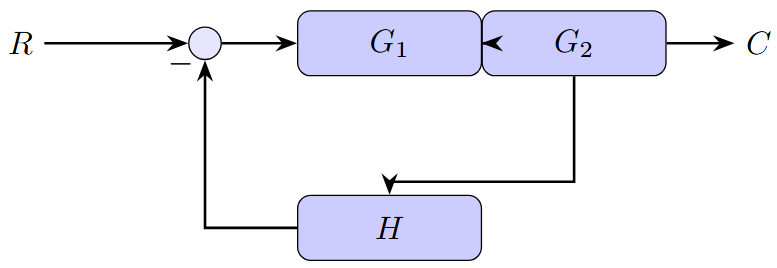
block_example

  1. \(\frac{6}{1+3}\)

  2. \(\frac{6}{1+6}\)

  3. \(\frac{6}{4}\)

  4. \(\frac{2}{3}\)

Solution

\[T(s) = \frac{G_1 G_2}{1 + G_1 G_2 H} = \frac{2 \times 3}{1 + 2 \times 3 \times 0.5} = \frac{6}{1 + 3} = \frac{6}{4} = 1.5\]
Answer: C

GATE Practice Questions - 6

Example

A second-order system has the transfer function:

\[G(s) = \frac{25}{s^2 + 4s + 25}\]
The natural frequency \(\omega_n\)and damping ratio \(\zeta\) are:

  1. \(\omega_n = 5\) rad/s, \(\zeta = 0.4\)

  2. \(\omega_n = 25\) rad/s, \(\zeta = 0.2\)

  3. \(\omega_n = 5\) rad/s, \(\zeta = 0.2\)

  4. \(\omega_n = 4\) rad/s, \(\zeta = 0.4\)

Solution

Standard form: \(G(s) = \frac{K\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2}\)

Comparing: \(\omega_n^2 = 25 \Rightarrow \omega_n = 5\) rad/s

\(2\zeta\omega_n = 4 \Rightarrow \zeta = \frac{4}{2 \times 5} = 0.4\)

Answer: A

Summary

Summary - Key Formulas

Transfer Function

\[G(s) = \frac{Y(s)}{X(s)} \text{ (zero initial conditions)}\]

Closed-Loop Transfer Function

\[T(s) = \frac{G(s)}{1 + G(s)H(s)} \text{ (negative feedback)}\]

Mason’s Gain Formula

\[T = \frac{1}{\Delta} \sum_{k=1}^{N} P_k \Delta_k\]

Error Constants

  • \(K_p = \lim_{s \to 0} G(s)H(s)\)

  • \(K_v = \lim_{s \to 0} s \cdot G(s)H(s)\)

  • \(K_a = \lim_{s \to 0} s^2 \cdot G(s)H(s)\)

Key Points for GATE EE

Important Concepts

  • Master block diagram reduction for complex systems

  • Understand Mason’s gain formula for signal flow graphs

  • Know system types and their error characteristics

  • Practice steady-state error calculations

  • Remember standard transfer function forms

Problem-Solving Strategy

  1. Identify system type and structure

  2. Choose appropriate analysis method (block diagram vs. Mason’s formula)

  3. Apply reduction rules systematically

  4. Verify results using alternative methods when possible

  5. Check units and limiting cases