Kirchhoff’s Laws
Kirchhoff’s Current Law (KCL)
Statement
The algebraic sum of currents entering a node is zero.
Mathematical Form:
Alternative Form:
Physical Basis: Conservation of charge
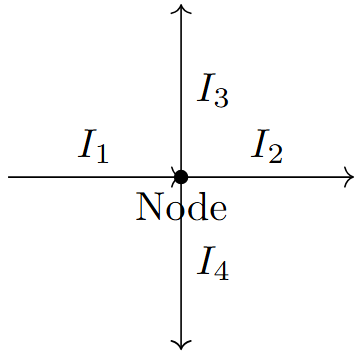
Example: \(I_1 - I_2 - I_3 - I_4 = 0\)
GATE Tip
Sign convention: Current entering = +ve, Current leaving = -ve
Kirchhoff’s Voltage Law (KVL)
Statement
The algebraic sum of voltages around any closed loop is zero.
Mathematical Form:
Physical Basis: Conservation of energy
Steps:
-
Choose loop direction
-
Apply sign convention
-
Write KVL equation
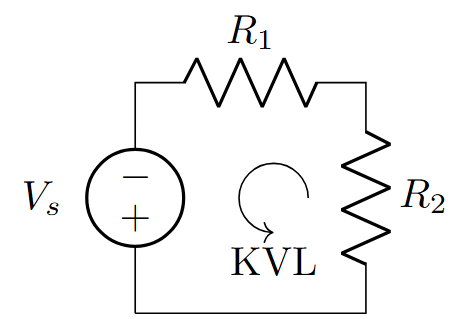
Example: \(V_s - I R_1 - I R_2 = 0\)
GATE Tip
Voltage rise = +ve, Voltage drop = -ve (or vice versa, be consistent)
Circuit Analysis Methods
Nodal Analysis
Procedure
-
Select reference node (ground)
-
Assign node voltages
-
Apply KCL at each non-reference node
-
Solve simultaneous equations
For node with voltage \(V_n\):
Supernode: When voltage source connects two non-reference nodes
When to Use
-
More current sources than voltage sources
-
Number of nodes < Number of meshes
-
Circuits with supernodes
GATE Formula: For n nodes, write (n-1) KCL equations
Mesh Analysis
Procedure
-
Identify independent meshes
-
Assign mesh currents (clockwise)
-
Apply KVL to each mesh
-
Solve simultaneous equations
For mesh with current \(I_m\):
Supermesh: When current source is common to two meshes
When to Use
-
More voltage sources than current sources
-
Number of meshes < Number of nodes
-
Planar circuits only
GATE Formula: For planar circuit: Meshes = Branches - Nodes + 1
Network Theorems
Superposition Theorem
Statement
In a linear circuit with multiple sources, the response is the algebraic sum of responses due to individual sources acting alone.
Procedure
-
Consider one source at a time
-
Replace other voltage sources with short circuits
-
Replace other current sources with open circuits
-
Calculate response due to active source
-
Repeat for all sources
-
Add all responses algebraically
GATE Important
-
Applicable only to LINEAR circuits
-
Power cannot be calculated using superposition
-
Dependent sources remain active
-
\(P_{total} \neq P_1 + P_2 + ... + P_n\)
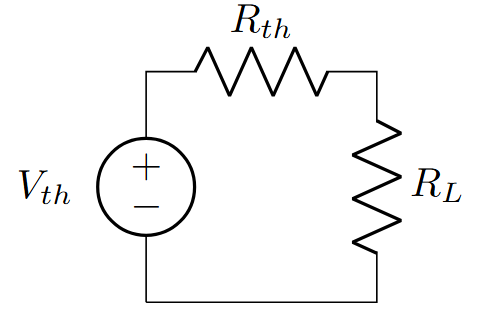
Thevenin’s Theorem
Statement
Any linear two-terminal network can be replaced by a voltage source \(V_{th}\) in series with resistance \(R_{th}\).
Steps:
-
Remove load resistance
-
Find \(V_{th}\) = Open circuit voltage
-
Find \(R_{th}\):
-
Kill independent sources
-
Look back into terminals
-
For dependent sources: \(R_{th} = \dfrac{V_{test}}{I_{test}}\)
-
-
Draw Thevenin equivalent
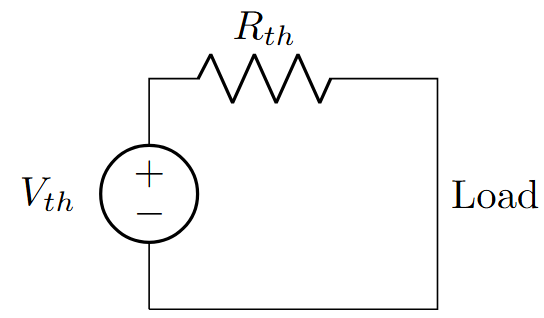
GATE Tip
Alternative method: \(R_{th} = \dfrac{V_{oc}}{I_{sc}}\) (open circuit voltage / short circuit current)
Norton’s Theorem
Statement
Any linear two-terminal network can be replaced by a current source \(I_N\) in parallel with resistance \(R_N\).
Steps:
-
Remove load resistance
-
Find \(I_N\) = Short circuit current
-
Find \(R_N = R_{th}\)
-
Draw Norton equivalent
Source Transformation:
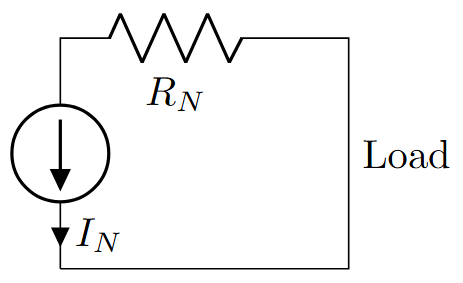
GATE Important
Norton and Thevenin are dual theorems. Use Norton when current calculation is easier.
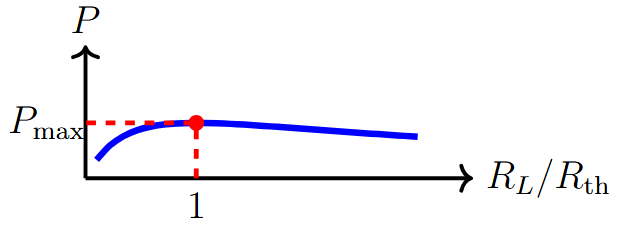
Maximum Power Transfer Theorem
Statement
Maximum power is transferred to load when load resistance equals source resistance.
Condition: \(R_L = R_{th}\)
Maximum Power:
Load Current:
Efficiency at Maximum Power:
GATE Note
For AC circuits: \(Z_L = Z_{th}^*\) (complex conjugate matching)
Additional Important Theorems
Reciprocity Theorem
Statement
In a linear, bilateral network, if a voltage source in branch A produces current in branch B, then the same voltage source in branch B will produce the same current in branch A.
Mathematical Form:
Transfer Impedance:
Conditions
-
Linear network
-
Bilateral elements (R, L, C)
-
No dependent sources
-
Same frequency for AC analysis
GATE Application: Useful in analyzing two-port networks and transmission lines.
Millman’s Theorem
Statement
Used to find voltage across parallel branches with different voltage sources.
Formula:
where \(V_k\) are source voltages, \(R_k\) are branch resistances, and \(G_k = \dfrac{1}{R_k}\) (conductance).
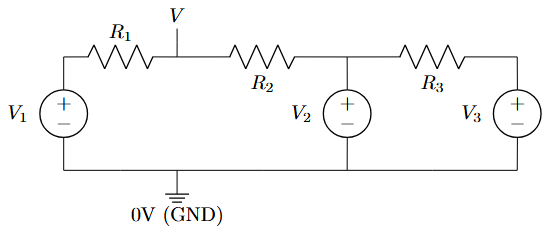
GATE Tip: Very useful for parallel voltage divider circuits and finding common voltage.
Compensation Theorem
Statement
When impedance in any branch changes from \(Z_1\) to \(Z_2\), the change in current can be calculated by considering a compensating voltage source.
Compensating Voltage:
where \(I_1\) is the original current through the branch.
Change in Current:
Applications
-
Fault analysis in power systems
-
Incremental analysis of circuits
-
Sensitivity analysis
-
Finding change in circuit parameters
GATE Usage: Useful for analyzing the effect of component variations on circuit behavior.
Substitution Theorem
Statement
Any branch in a network can be replaced by an equivalent branch that has the same voltage across it and current through it.
Equivalent Replacements:
-
Voltage source = Branch voltage (\(V_s = V_{branch}\))
-
Current source = Branch current (\(I_s = I_{branch}\))
-
Impedance = \(Z_{eq} = \dfrac{V_{branch}}{I_{branch}}\)
GATE Application
Very useful for:
-
Simplifying complex circuits
-
Finding equivalent circuits
-
Network reduction techniques
-
Analyzing one part of circuit independently
Note: The rest of the circuit behavior remains unchanged.
Tellegen’s Theorem
Statement
In any lumped network, the sum of instantaneous powers delivered to all branches is zero.
Mathematical Form:
Physical Interpretation: Total power generated = Total power consumed
Applications
-
Power balance verification
-
Network analysis validation
-
Fundamental theorem for all network theorems
-
Circuit simulation algorithms
GATE Importance
Tellegen’s theorem is the most fundamental theorem - all other network theorems can be derived from it.
Star-Delta Transformation
Statement
Any three-terminal star (Y) network can be transformed to equivalent delta (\(\Delta\)) network and vice versa.
Star to Delta:
General Form:
Delta to Star:
General Form:
GATE Tip
For equal resistances: \(R_Y = \dfrac{R_\Delta}{3}\) and \(R_\Delta = 3R_Y\)
Advanced Concepts
Dependent Sources and Network Theorems
Key Points
-
Dependent sources are never killed/deactivated
-
They remain active during Thevenin/Norton analysis
-
Superposition: Only independent sources are considered one at a time
-
For \(R_{th}\) with dependent sources: Apply test voltage/current method
Test Source Method:
-
Kill all independent sources
-
Apply test voltage \(V_t\) (or current \(I_t\))
-
Calculate resulting current \(I_t\) (or voltage \(V_t\))
-
\(R_{th} = \dfrac{V_t}{I_t}\)
GATE Common Error
Students often try to kill dependent sources - this is incorrect!
AC Circuit Analysis
Impedance Form
All theorems apply to AC circuits using complex impedances:
-
Resistance \(R ~\to\) Impedance \(Z\)
-
DC voltage/current \(\to\) Phasor voltage/current
-
\(R_{th}\) becomes \(Z_{th}\)
Maximum Power Transfer (AC):
Phasor Analysis:
-
Use \(j\omega L\) for inductors
-
Use \(\dfrac{1}{j\omega C}\) for capacitors
-
All calculations in complex domain
GATE Tip
For purely resistive loads: \(R_L = |Z_{th}|\) for maximum power transfer
Quick Reference
GATE Quick Reference Card
Key Formulas
-
KCL: \(\sum I = 0\) at any node
-
KVL: \(\sum V = 0\) around any loop
-
Thevenin: \(V_{th}\) (open circuit), \(R_{th}\) (kill sources or \(V_{oc}/I_{sc}\))
-
Norton: \(I_N\) (short circuit), \(R_N = R_{th}\)
-
Max Power: \(R_L = R_{th}\), \(P_{max} = \dfrac{V_{th}^2}{4R_{th}}\), \(\eta = 50\%\)
-
Millman: \(V = \dfrac{\sum G_k V_k}{\sum G_k}\)
-
Star-Delta: \(R_Y = \dfrac{R_\Delta}{3}\) (equal resistances)
Method Selection
-
Nodal: More current sources, fewer nodes
-
Mesh: More voltage sources, planar circuit
-
Thevenin/Norton: Load analysis, source equivalents
-
Superposition: Multiple sources, linear circuits
-
Star-Delta: Non-planar circuits, bridge circuits
Common GATE Problem Types
Numerical Problems
-
Direct Application: Find current/voltage using specific theorem
-
Equivalent Circuits: Thevenin/Norton equivalents
-
Maximum Power: Load resistance and power calculations
-
Comparative Analysis: Which method is most efficient?
-
Mixed Circuits: AC and DC sources, dependent sources
-
Network Simplification: Using multiple theorems
Common GATE Mistakes
-
Killing dependent sources in Thevenin analysis
-
Using superposition for power calculations
-
Wrong sign conventions in KCL/KVL
-
Forgetting complex conjugate in AC maximum power transfer
-
Not considering all constraint equations in supernode/supermesh
Time-Saving Techniques
Quick Methods
-
Voltage Divider: \(V_R = V_s \dfrac{R}{R_{total}}\)
-
Current Divider: \(I_R = I_s \dfrac{R_{other}}{R + R_{other}}\)
-
Source Transformation: Convert between voltage and current sources
-
Series/Parallel Combinations: Simplify before applying theorems
-
Symmetry: Use circuit symmetry to reduce calculations
GATE Strategy
-
Identify the quickest method first (30 seconds)
-
Check if answer choices give clues about approach
-
Use approximations when exact values aren’t needed
-
Verify answers using alternative methods if time permits
Memory Aids
Mnemonics
-
KCL: "Current In = Current Out"
-
KVL: "Voltage Rises = Voltage Falls"
-
Thevenin: "Open circuit voltage, Kill sources for resistance"
-
Norton: "Short circuit current, Same resistance"
-
Max Power: "Match the load, Get half efficiency"
-
Superposition: "One source at a time, others killed"
Quick Checks
-
Power balance: \(\sum P_{generated} = \sum P_{consumed}\)
-
Dimension analysis: Check units in final answer
-
Limiting cases: What happens when \(R \to 0\) or \(R \to \infty\)?
-
Symmetry: Equal components should have equal currents/voltages