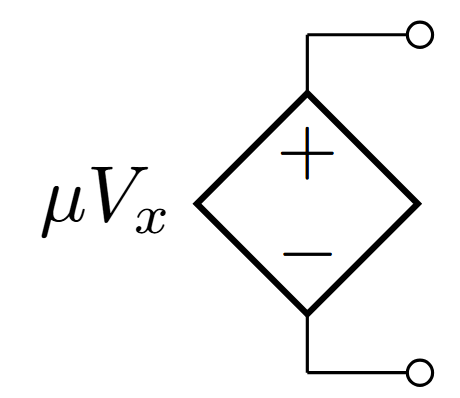Network Elements Notes for GATE Electrical Engineering (EE)

Ideal Voltage Sources

Ideal Voltage Source

Definition:

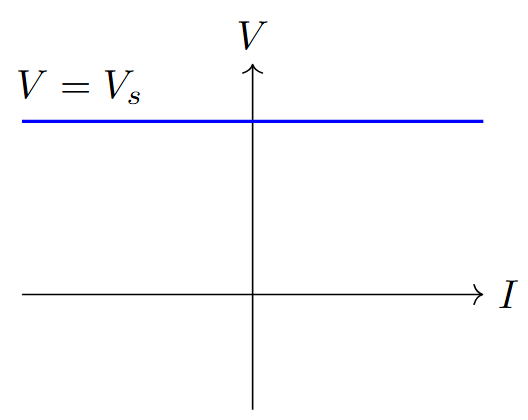
  • Maintains constant voltage across terminals

  • Independent of current through it

  • Internal resistance = 0

Key Properties:

  • \(V = V_s\) (constant)

  • Current \(I\) can be any value

  • Power delivered: \(P = V_s \cdot I\)

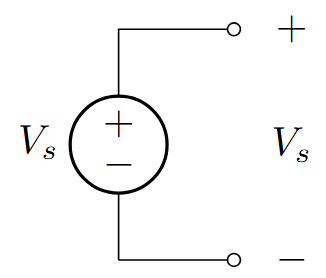
Ideal voltage source
Ideal voltage source
Ideal voltage characteristic
Ideal voltage characteristic

Ideal Current Sources

Ideal Current Source

Definition:

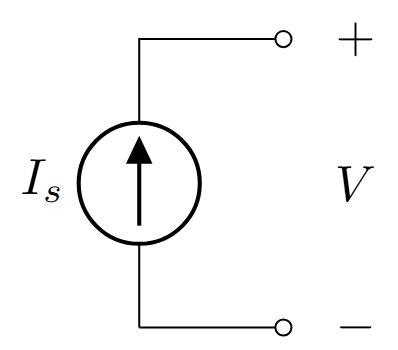
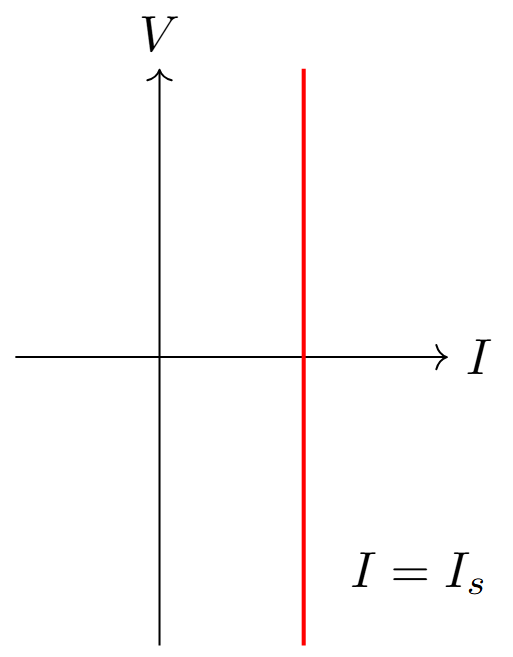
  • Maintains constant current through terminals

  • Independent of voltage across it

  • Internal resistance = \(\infty\)

Key Properties:

  • \(I = I_s\) (constant)

  • Voltage \(V\) can be any value

  • Power delivered: \(P = V \cdot I_s\)

Ideal current source
Ideal current source
Ideal curent characteristic
Ideal curent characteristic

Dependent Sources

Dependent Sources - Types

  • Voltage Controlled Voltage Source (VCVS)

    Voltage Controlled Voltage Source
    Voltage Controlled Voltage Source

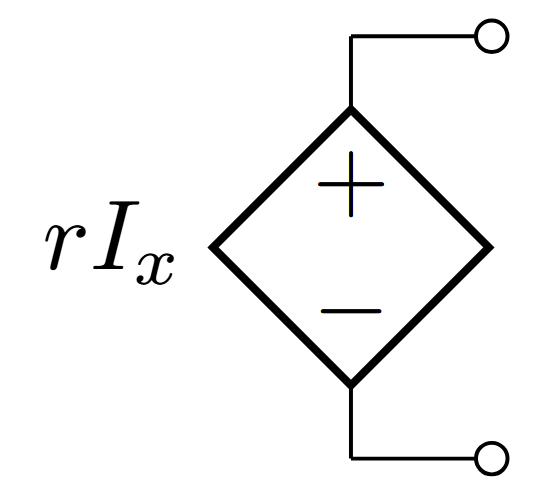
  • Current Controlled Voltage Source (CCVS)

    Current Controlled Voltage Source
    Current Controlled Voltage Source

  • Voltage Controlled Current Source (VCCS)

    Voltage Controlled Current Source
    Voltage Controlled Current Source

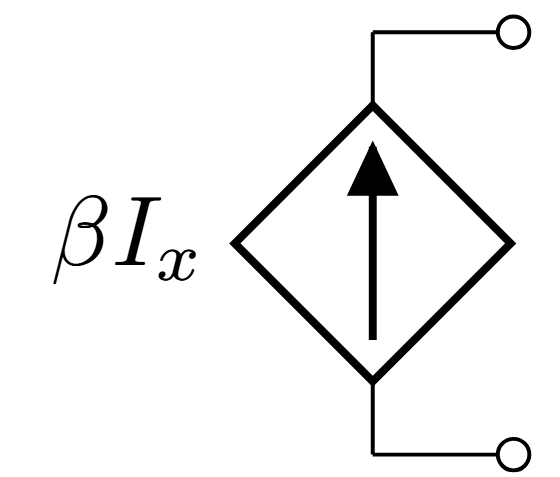
  • Current Controlled Current Source (CCCS)

    Current Controlled Current Source
    Current Controlled Current Source

Resistor (R)

Resistor - Properties

Ohm’s Law:

\[V = IR \quad \text{or} \quad I = \frac{V}{R}\]

Power Relations:

\[P = VI = I^2R = \frac{V^2}{R}\]

Key Properties:

  • Linear element

  • Passive element (absorbs power)

  • Instantaneous relationship

  • Energy is dissipated as heat

Series & Parallel:

  • Series: \(R_{eq} = R_1 + R_2 + \ldots\)

  • Parallel: \(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots\)

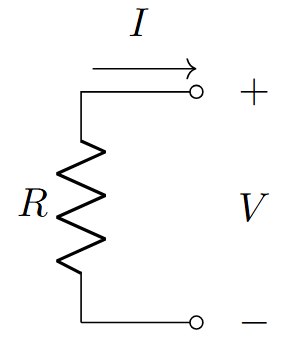
Voltage and current in a resistor
Voltage and current in a resistor
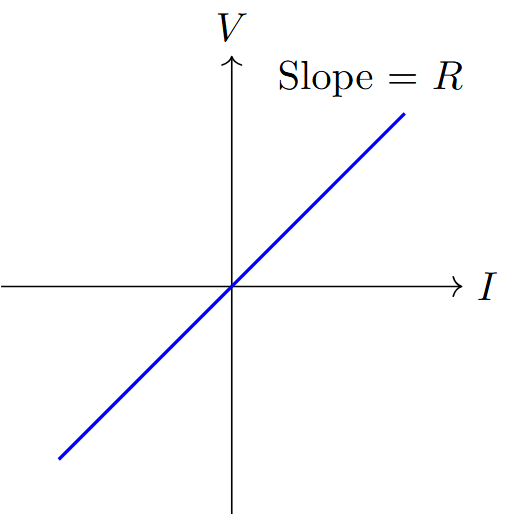
VI characteristics of a Resistor
VI characteristics of a Resistor

Inductor (L)

Inductor - Properties

V-I Relationship:

\[V = L\frac{di}{dt}\]
\[I = \frac{1}{L}\int_0^t V \, d\tau + I(0)\]

Energy Stored:

\[W = \frac{1}{2}LI^2\]

Key Properties:

  • Reactive element

  • Opposes change in current

  • Current cannot change instantaneously

  • \(I(0^-) = I(0^+)\) (continuity)

  • Stores magnetic energy

Series & Parallel:

  • Series: \(L_{eq} = L_1 + L_2 + \ldots\)

  • Parallel: \(\frac{1}{L_{eq}} = \frac{1}{L_1} + \frac{1}{L_2} + \ldots\)

Inductor voltage and current relationship
Inductor voltage and current relationship

AC Impedance:

\[Z_L = j\omega L\]

DC Behavior:

  • Steady state: Short circuit

  • \(\frac{di}{dt} = 0 \Rightarrow V = 0\)

Capacitor (C)

Capacitor - Properties

V-I Relationship:

\[I = C\frac{dv}{dt}\]
\[V = \frac{1}{C}\int_0^t I \, d\tau + V(0)\]

Energy Stored:

\[W = \frac{1}{2}CV^2\]

Key Properties:

  • Reactive element

  • Opposes change in voltage

  • Voltage cannot change instantaneously

  • \(V(0^-) = V(0^+)\) (continuity)

  • Stores electric energy

Series & Parallel:

  • Series: \(\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \ldots\)

  • Parallel: \(C_{eq} = C_1 + C_2 + \ldots\)

Capacitor voltage and current relationship
Capacitor voltage and current relationship

AC Impedance:

\[Z_C = \frac{1}{j\omega C} = -j\frac{1}{\omega C}\]

DC Behavior:

  • Steady state: Open circuit

  • \(\frac{dv}{dt} = 0 \Rightarrow I = 0\)

Mutual Inductance (M)

Mutual Inductance - Coupled Coils

Coupled Equations:

\[V_1 = L_1\frac{di_1}{dt} \pm M\frac{di_2}{dt}\]
\[V_2 = L_2\frac{di_2}{dt} \pm M\frac{di_1}{dt}\]

Coupling Coefficient:

\[k = \frac{M}{\sqrt{L_1 L_2}} \quad (0 \leq k \leq 1)\]

Energy Stored:

\[W = \frac{1}{2}L_1i_1^2 + \frac{1}{2}L_2i_2^2 \pm Mi_1i_2\]

Dot Convention:

  • Same dot: \(+M\) (aiding)

  • Different dot: \(-M\) (opposing)

Mutually coupled coils
Mutually coupled coils

AC Analysis:

\[Z_{11} = j\omega L_1\]
\[Z_{22} = j\omega L_2\]
\[Z_{12} = Z_{21} = \pm j\omega M\]

Summary Table

Network Elements - Summary

Element V-I Relation Power Energy AC Impedance
Resistor \(V = IR\) \(P = I^2R\) Dissipated \(R\)
Inductor \(V = L\frac{di}{dt}\) \(P = Vi\) \(W = \frac{1}{2}LI^2\) \(j\omega L\)
Capacitor \(I = C\frac{dv}{dt}\) \(P = Vi\) \(W = \frac{1}{2}CV^2\) \(\frac{1}{j\omega C}\)
Voltage Source \(V = V_s\) \(P = V_s I\) - -
Current Source \(I = I_s\) \(P = V I_s\) - -

Important GATE Points:

  • Initial conditions for L and C

  • Series/parallel combinations

  • Dependent source analysis

  • Energy and power calculations

  • AC impedance concepts