Introduction
-
Operational amplifiers are fundamental building blocks in electronics
-
Basic and special purpose op-amp circuits:
-
Comparators
-
Summing amplifiers
-
Integrators and differentiators
-
Instrumentation amplifiers
-
Specialized amplifiers (OTA, log/antilog)
-
-
Applications include signal processing, digital circuits, and analog-to-digital conversion
Comparators
-
Specialized op-amp circuit that compares two input voltages
-
Output is always in one of two states (high or low)
-
Key characteristics:
-
Very fast switching times (as low as 500 ps propagation delay)
-
High open-loop gain enables detection of tiny input differences
-
-
Used for analog-to-digital interfacing
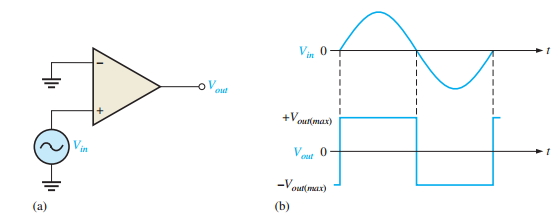
Zero-Level Detection
-
Inverting input grounded (0 V reference)
-
Input signal applied to noninverting input
-
Smallest input difference drives amplifier to saturation
-
Can convert sine waves to square waves (squaring circuit)
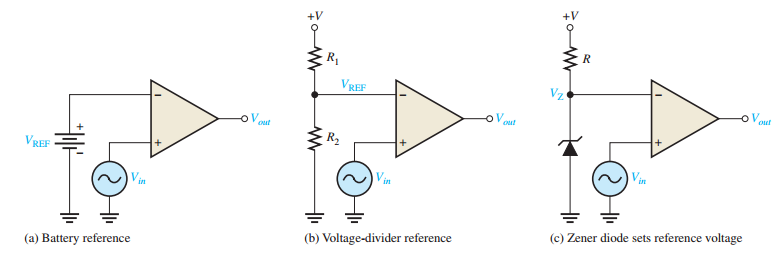
Nonzero-Level Detection
-
Fixed reference voltage replaces ground at inverting input
-
Three reference voltage methods:
-
Battery reference
-
Voltage divider reference (\(V_{REF} = \dfrac{R_2}{R_1+R_2}(+V)\))
-
Zener diode reference (\(V_{REF} = V_Z\))
-
-
Output switches when input crosses \(V_{REF}\)
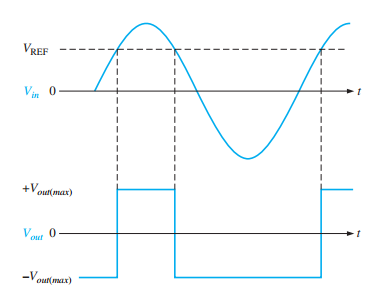
Given \( R_1 = 8.2k\Omega \), \( R_2 = 1.0k\Omega \), \( +V = 15V \):
\[ V_{REF} = \frac{1.0k\Omega}{8.2k\Omega + 1.0k\Omega}(15V) = 1.63V \]
Output switches between \( \pm 14V \) when input crosses 1.63V.
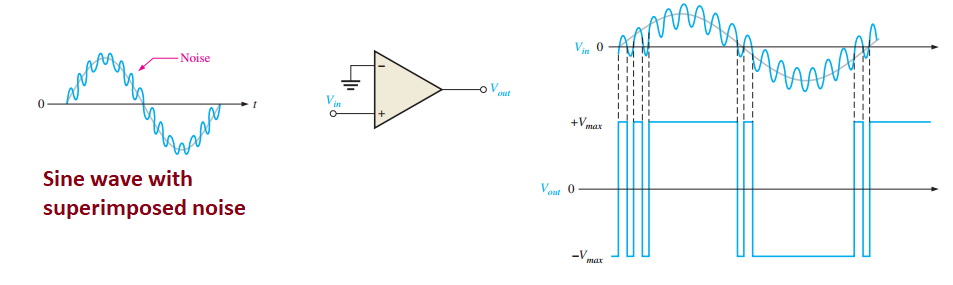
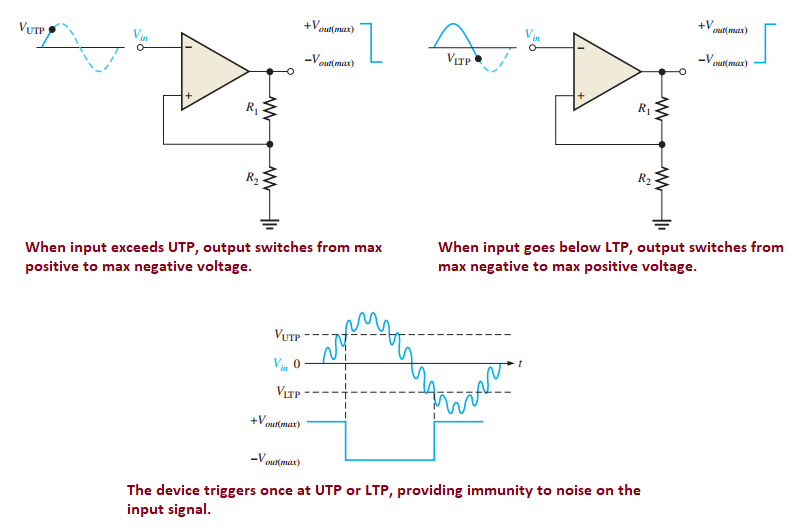
Noise Effects and Hysteresis
-
Noise (unwanted voltage fluctuations) can cause unstable switching near the threshold
-
Example: A low-frequency sinusoidal voltage with noise causes erratic output
-
Solution: Implement hysteresis using positive feedback
-
Upper Trigger Point (UTP): \(V_{UTP} = \dfrac{R_2}{R_1+R_2}(+V_{out(max)})\)
-
Lower Trigger Point (LTP): \(V_{LTP} = \dfrac{R_2}{R_1+R_2}(-V_{out(max)})\)
-
Hysteresis voltage: \(V_{HYS} = V_{UTP} - V_{LTP}\)
-
-
Also called a Schmitt trigger
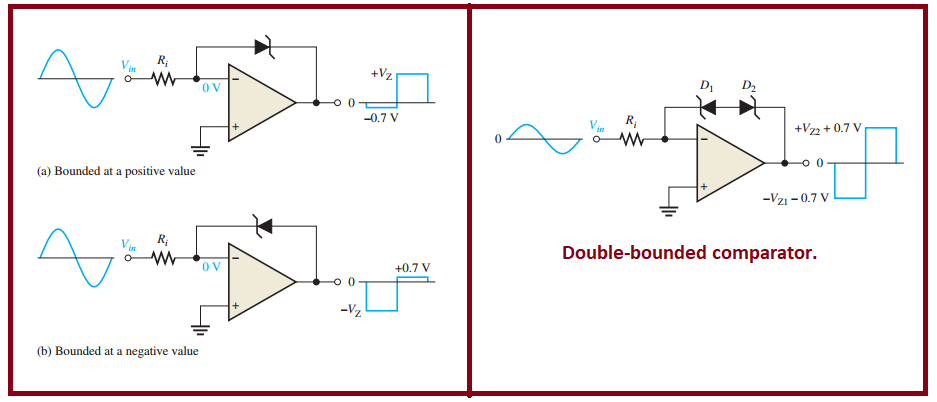
Output Bounding
-
Limits output voltage to values less than op-amp saturation
-
Methods:
-
Single zener diode: bounds one direction
-
Two zener diodes: bounds both directions (\(V_Z + 0.7V\) each way)
-
-
Example: With 4.7V zeners, output bounds at \(\pm5.4V\)
Comparator Applications
-
Over-temperature sensing:
-
Uses Wheatstone bridge with thermistor
-
Comparator detects bridge balance point
-
Triggers alarm/response when temperature exceeds threshold
-
-
Analog-to-Digital Conversion (Flash ADC):
-
Uses parallel comparators with reference voltage ladder
-
\(2^n-1\) comparators needed for n-bit conversion
-
Priority encoder produces binary output
-

Amplifiers
Summing Amplifier
-
Application of inverting op-amp configuration
-
Output proportional to negative sum of input voltages
-
\[\begin{aligned} V_{OUT} = -\left(\dfrac{R_f}{R_1}V_{IN1} + \dfrac{R_f}{R_2}V_{IN2} + \cdots + \dfrac{R_f}{R_n}V_{INn}\right) \end{aligned}\]General output equation:
-
\[\begin{aligned} V_{OUT} = -\dfrac{R_f}{R}(V_{IN1} + V_{IN2} + \cdots + V_{INn}) \end{aligned}\]For equal input resistors

Unity-Gain Summing Amplifier
-
Special case where \(R_f = R\)
-
\[\begin{aligned} V_{OUT} = -(V_{IN1} + V_{IN2} + \cdots + V_{INn}) \end{aligned}\]Output is simple inverted sum of inputs:
-
\[\begin{aligned} V_{OUT} = -(2V - 3V + 4V) = -3V \end{aligned}\]Example: For inputs +2V, -3V, and +4V:
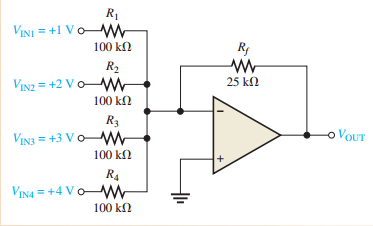
Averaging Amplifier
-
Produces mathematical average of input voltages
-
Set \(R_f/R = 1/n\) where \(n\) is number of inputs
-
\[\begin{aligned} V_{OUT} = -\dfrac{1}{n}(V_{IN1} + V_{IN2} + \cdots + V_{INn}) \end{aligned}\]Output equation:
-
\[\begin{aligned} V_{OUT} = -\dfrac{25k\Omega}{100k\Omega}(V_1 + V_2 + V_3 + V_4) = -\dfrac{1}{4}(V_1 + V_2 + V_3 + V_4) \end{aligned}\]: , Example: 4-input averager with
Digital-to-Analog Conversion
-
Binary-weighted resistor DAC:
-
Each input resistor corresponds to binary weight
-
MSB has smallest resistor (\(R\)), next has \(2R\), then \(4R\), etc.
-
Output is analog representation of digital input
-
-
R/2R ladder DAC:
-
Uses only two resistor values (\(R\) and \(2R\))
-
More practical for IC implementation
-
Each bit contributes half the voltage of the previous bit
-

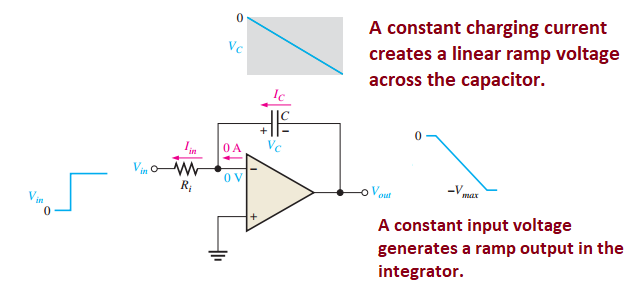
Op-Amp Integrator
-
Produces output proportional to integral of input
-
Basic configuration:
-
Input resistor \(R_{in}\)
-
Feedback capacitor \(C\)
-
-
\[\begin{aligned} V_{OUT} = -\dfrac{1}{R_{in}C}\int V_{IN} dt \end{aligned}\]Output voltage:
-
Constant input produces linear ramp output
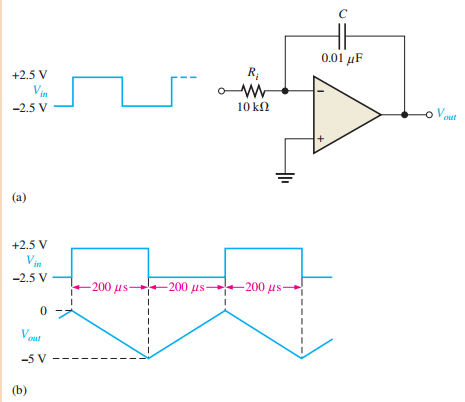
Op-Amp Integrator Example
Given \( R_{in} = 10k\Omega \), \( C = 0.01\mu F \), square wave input \( \pm 2.5V \):
\[ \frac{\Delta V_{out}}{\Delta t} = -\frac{V_{in}}{R_{in}C} = -\frac{2.5V}{10k\Omega \times 0.01\mu F} = -25mV/\mu s \]
Produces triangular wave output with 5V peak-to-peak.
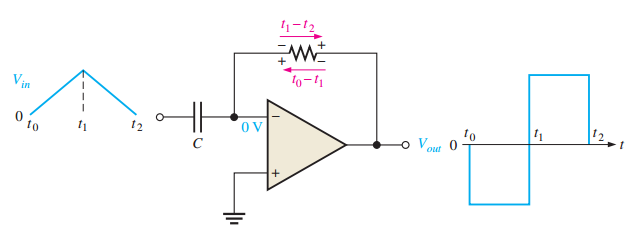
Op-Amp Differentiator
-
Produces output proportional to derivative of input
-
Basic configuration:
-
Input capacitor \(C\)
-
Feedback resistor \(R_f\)
-
-
Output voltage:
-
\[\begin{aligned} V_{OUT} = -R_f C \dfrac{dV_{IN}}{dt} \end{aligned}\]
-
Ramp input produces constant output
Instrumentation Amplifiers
-
Amplify small signals riding on large common-mode voltages
-
Key Characteristics:
-
High input impedance
-
High common-mode rejection
-
Low output offset
-
Low output impedance
-
-
\[\begin{aligned} \text{Gain}~A_{cl} = 1 + \dfrac{2R}{R_{\text{gain}}} \quad \text{where} \quad R_1 = R_2 = R \end{aligned}\]
-
Input Stage (2 Op-Amps): High \(Z_{in}\) and initial amplification
-
Difference Amplifier (3rd Op-Amp): Subtracts and amplifies input signal difference

Specialized Circuits
Operational Transconductance Amplifier (OTA)
-
OTA is a voltage-controlled current source (VCCS)
-
\[\begin{aligned} I_{\text{out}} = g_m \cdot (V_+ - V_-) \end{aligned}\]: into output Converts differential input
-
Output is current, unlike op-amps which output voltage
-
Transconductance \(g_m\) is programmable via bias current
-
Key Characteristics:
-
High input impedance
-
Wide bandwidth
-
Linear transconductance over bias range
-
Suitable for analog signal processing
-
OTA Applications and Comparison
Applications:
-
Voltage-controlled filters and oscillators
-
Analog multipliers and dividers
-
Audio and RF processing
-
AGC circuits, function generators
OTA vs Op-Amp:
| Feature | OTA | Op-Amp |
|---|---|---|
| Output | Current | Voltage |
| Controlled by | Bias current (\(g_m\)) | Open-loop gain |
| Key Parameter | \(g_m\) (transconductance) | \(A_{OL}\) (gain) |
| Primary Use | Tunable analog circuits | Voltage amplification |
Logarithmic Amplifier (Log Amp)
-
Outputs a voltage proportional to the logarithm of the input voltage
-
\[\begin{aligned} V_{\text{out}} = -K \cdot \ln\left(\dfrac{V_{\text{in}}}{V_T}\right) \end{aligned}\]Based on the exponential I-V relationship of a diode or BJT:
-
Uses an op-amp with a diode or BJT in the feedback path
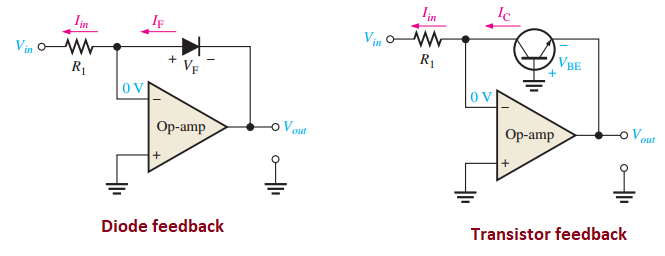
Antilogarithmic Amplifier (Antilog Amp)
-
Converts a logarithmic input back to a linear output
-
\[\begin{aligned} V_{\text{out}} = K \cdot e^{V_{\text{in}}/V_T} \end{aligned}\]Uses a transistor in the input path to create an exponential relationship:
-
\[\begin{aligned} \log(A) + \log(B) = \log(AB) \Rightarrow \text{Antilog} \rightarrow AB \end{aligned}\]Often paired with log amps for analog multiplication/division:
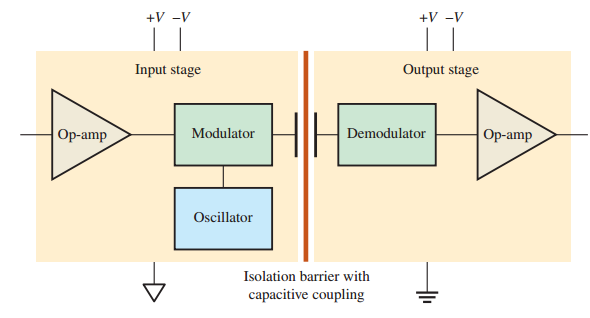
Isolation Amplifier
-
Transmits signals across two circuits with galvanic isolation
-
Prevents high voltages or ground loop currents from damaging systems
-
Isolation achieved using:
-
Transformer coupling
-
Optical isolation (optocouplers)
-
Capacitive coupling
-
-
Key Features:
-
High input-to-output isolation voltage
-
Accurate signal transmission
-
High common-mode rejection (CMR)
-
Isolation Amplifier Applications
-
Applications:
-
Medical instrumentation (e.g., ECG, EEG)
-
Industrial process control
-
High-voltage system monitoring
-
Signal isolation in data acquisition systems
-
-
Advantages:
-
Protects measurement devices from voltage spikes
-
Eliminates ground loops and electrical noise
-
Enables safe measurement in hazardous environments
-
-
Note: Often integrated with analog-to-digital converters (ADCs)
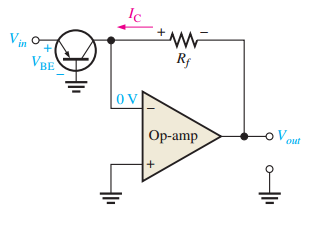
Constant-Current Source
-
Delivers a fixed current regardless of load resistance
-
Based on Ohm’s law: \(I = \dfrac{V_{\text{ref}}}{R}\)
-
Uses negative feedback to maintain stable output current

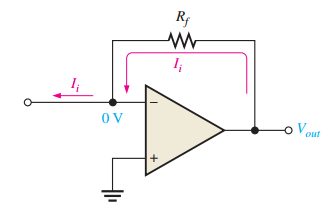
Current-to-Voltage Converter
-
Also called a Transimpedance Amplifier
-
Converts input current (\(I_{\text{in}}\)) to output voltage (\(V_{\text{out}}\))
-
Output: \(V_{\text{out}} = -I_{\text{in}} R_f\)
-
Commonly used with photodiodes and sensors
Voltage-to-Current Converter
-
Also called a Voltage-Controlled Current Source (VCCS)
-
Converts input voltage to output current
-
Output current: \(I_{\text{out}} = \dfrac{V_{\text{in}}}{R}\)
-
Useful in actuators and LED drivers

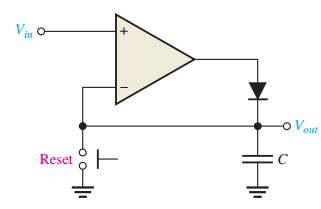
Peak Detector
-
Captures and holds the peak value of an input signal
-
Uses an op-amp, diode, and capacitor
-
Commonly used in signal processing and instrumentation
Conclusion
-
Operational amplifiers are versatile components in electronics, enabling a wide range of circuits:
-
Comparators for signal comparison and ADC interfacing
-
Summing, averaging, and DAC circuits for signal processing
-
Integrators and differentiators for waveform generation
-
Instrumentation amplifiers for precise measurements
-
Specialized circuits (OTA, log/antilog, isolation) for advanced applications
-
-
Their high gain, flexibility, and reliability make op-amps essential in modern electronics
-
Future exploration: Advanced op-amp designs and integration with digital systems