Unveiling Diodes: A Comprehensive Guide to Diode Theory (Electronics)

Demonstrative Video

Need for a Diode - Initial Thoughts

Charger Circuit Operation

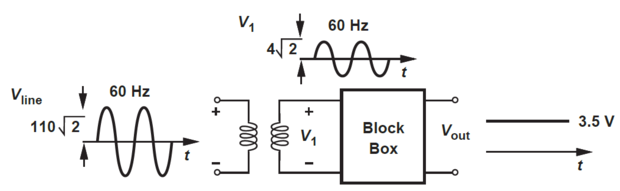
\(\xrightarrow[\text{110 V}]{\text{ac voltage}}\) \(\xrightarrow[\text{4 V}]{\text{Transformer}}\) \(\xrightarrow[\text{3.5 V}]{\text{dc voltage using LPF}}\)
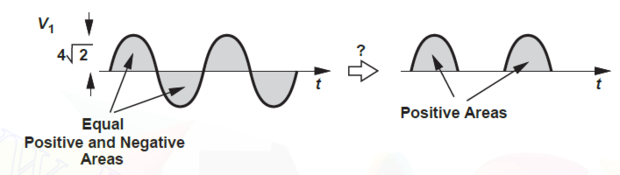
Output of TF using black box exhibits a zero dc content as -ve and +ve half cycles enclose equal areas, leading to a zero average

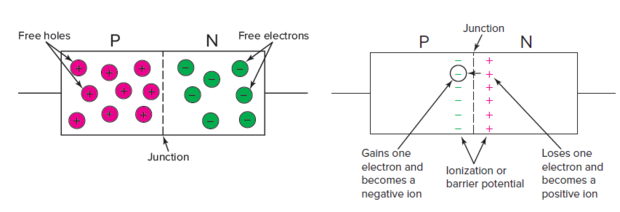
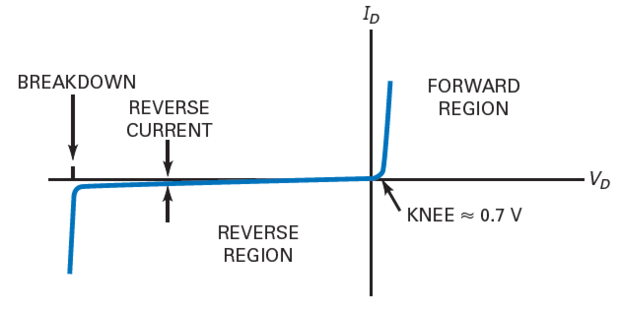
DIODE - Basic Ideas

Resistor \(\rightarrow\) linear device \(\rightarrow\) current Vs voltage is a straight line.
Diode \(\rightarrow\) nonlinear device \(\rightarrow\) \(I\) Vs \(V\) is not a straight line.
The reason is the barrier potential.

\[\boxed{V_d < V_b \rightarrow I_d \downarrow} \qquad \boxed{V_d > V_b \rightarrow I_d \uparrow}\]

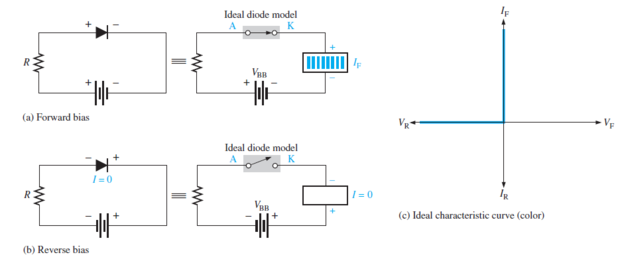
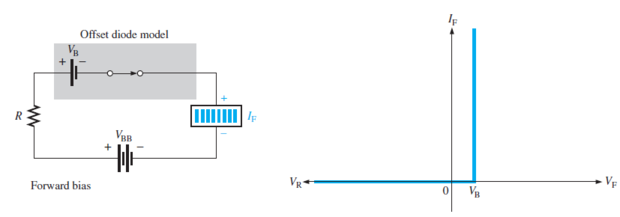
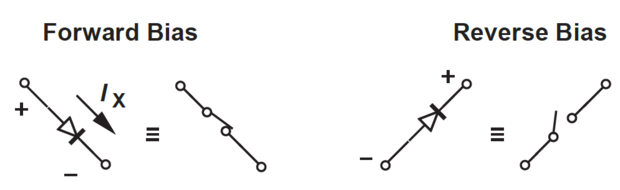
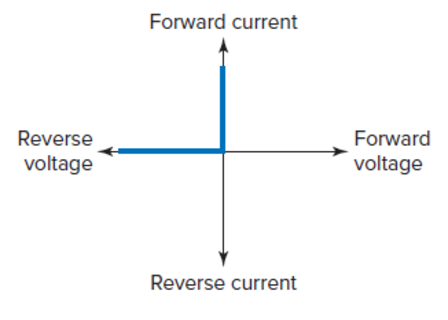
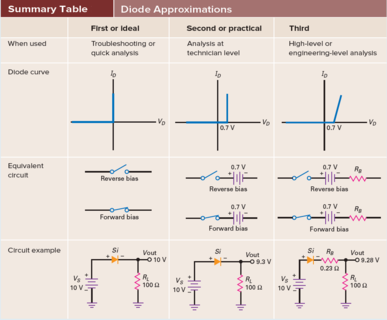
Ideal Diode: acts like a perfect conductor (zero resistance) when forward biased and like a perfect insulator (\(\infty\) resistance) when reverse biased.

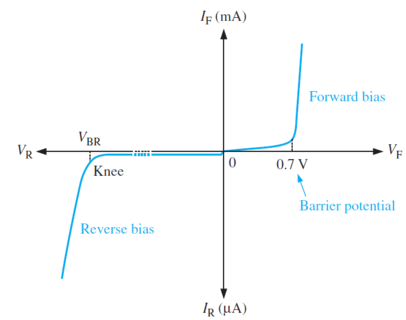
Diode Characteristic Curve

\[\begin{aligned} & V_{\text{anode}} > V_{\text{cathode}} \leftarrow \text{on} \\ & V_{\text{anode}} < V_{\text{cathode}} \leftarrow \text{off} \\ & V_{\text{anode}} - V_{\text{cathode}} = V_D \end{aligned}\]

Real diode

Ideal diode

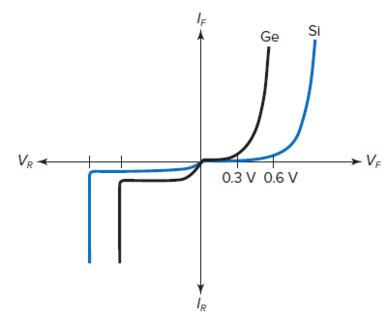
Si Vs Ge

Above the knee voltage, the diode current increases rapidly.
Small increase in the diode voltage cause large increases in diode current.

\[\text{Bulk resistance}~R_B = R_p + R_n\]
. is less than 1 depends on the size of the p and n regions and how heavily doped they are. Often, Bulk Resistance :
Maximum DC Forward Current : If the current in a diode is too large, the excessive heat can destroy the diode. The \(I_{F(max)}\) is one of the maximum ratings given on a data sheet.
\[\begin{aligned} P_D & = V_D \cdot I_D \\ P_{max} & = V_{max} \cdot I_{max} \end{aligned}\]
The power rating is the maximum power the diode can safely dissipate without shortening its life or degrading its propertiesPower Dissipation :

Diode Current Equation

\[I=I_o\left[\mathrm{e}^{\left(V / \eta V_T\right)}-1\right]\]

\[\begin{aligned} I & = \text{diode current} \\ I_o & = \text{diode reverse saturation current at room temperature}\\ V & = \text{external voltage applied to the diode} \\ \eta &=\text{ a constant, 1 for germanium and 2 for silicon} \\ V_T&=k T / q=T / 11600, \text{volt-equivalent of temperature, i.e., thermal voltage} \\ k & = \text{Boltzmann's constant}~\left(1.38066 \times 10^{-23} \mathrm{~J} / \mathrm{K}\right)\\ q & = \text{charge of the electron}~ \left(1.60219 \times 10^{-19} \mathrm{C}\right)\\ T & = \text{temperature of the diode junction}~ (\mathrm{K})=\left({ }^{\circ} \mathrm{C}+273^{\circ}\right) \end{aligned}\]

and current The diode current equation relating the voltage

\[\boxed{I=I_o\left[\mathrm{e}^{\left(V / \eta V_T\right)}-1\right]}\]

When the diode is reverse biased, its current equation may be obtained by changing the sign of the applied voltage \(V\).
\[I=I_o\left[\mathrm{e}^{\left(-V / \eta V_T\right)}-1\right]\]
Thus, the diode current with reverse bias is
If \(V \gg V_T\), then the term \(\mathrm{e}^{\left(-V / \eta v_T\right)} \ll 1\), therefore \(I \approx-I_o\), termed as reverse saturation current, which is valid as long as the external voltage is below the breakdown value.

Effect of temperature:

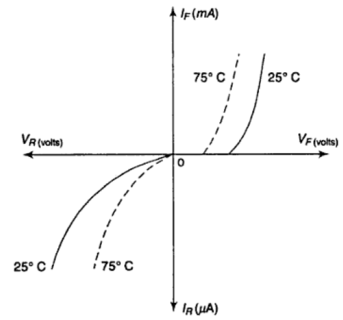
T \(\uparrow~\Rightarrow\) generation of e-p pairs increases, which increase the conductivities
If T \(\uparrow\) at fixed V \(\Rightarrow\) I increases
To bring I to normal \(\Rightarrow\) V \(\downarrow\)

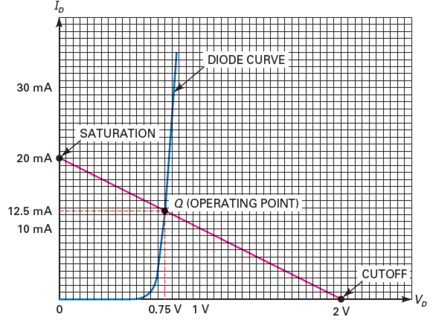
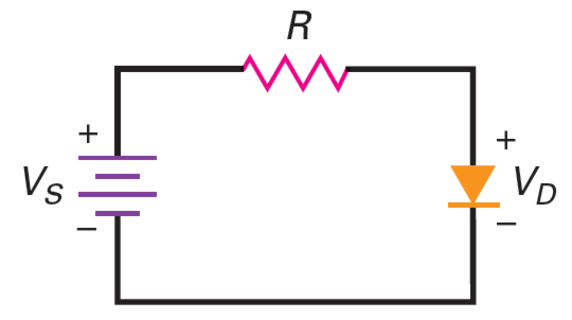
Load Lines

\[I_D=\frac{V_S-V_D}{R_s}\]
Load line

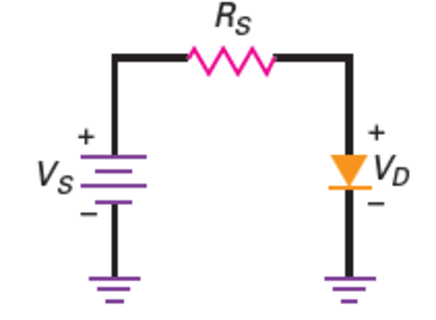
If \(V_s = 2~\mathrm{V}\), \(R = 100~\Omega\)
\(V_D = 0 \Rightarrow I_D = 20~\mathrm{mA}\)
\(I_D = 0 \Rightarrow V_D = V_s = 2~\mathrm{V}\)
The straight line is called the load line
\(Q\) is an abbreviation for quiescent, which means “at rest.”