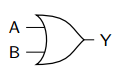
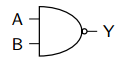
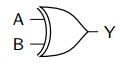
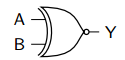
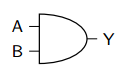
Problem 19: AND Gate
Definition
AND gate produces output 1 only when ALL inputs are 1.
Boolean Expression:
\(Y = A \cdot B\) or \(Y = AB\)
Truth Table
| A | B | Y = A·B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Applications
-
Enable/Disable circuits
-
Masking operations
-
Multiplication in arithmetic circuits