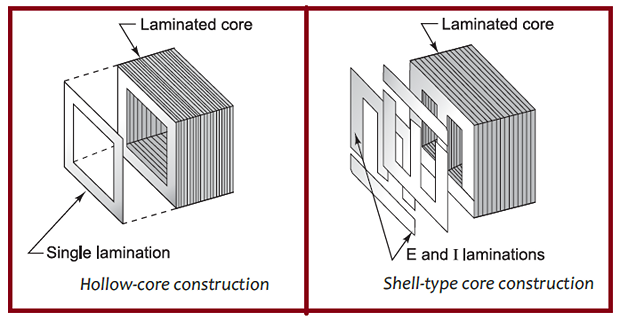
two main shapes of cores used in laminated steel-core transformers
Construction
Working Principle
EMF Equation
Transformation Ratio (K)
Rating of a Transformer
Losses in a Transformer
Ideal and Practical Transformers
Phasor Diagram of a Transformer on No Load
Phasor Diagram of a Transformer on Load
Equivalent Circuit
Voltage Regulation
Efficiency
Open Circuit (OC) Test and Short-Circuit (SC) Test
Static device which can transfer electrical energy from one circuit to another circuit without change of frequency.
\(V~\uparrow~\Rightarrow~I~\downarrow\) and vice versa
Works on the principle of mutual induction.
Works with ac voltage i.e. time varying.
A major application is to increase voltage before transmitting electrical energy over long distances through wires and to reduce voltage at places where it is to be used.
Used in electronic circuits to step down the supply voltage to a level suitable for the low-voltage circuits they contain.
Signal and audio transformers are used to couple stages of amplifiers and to match devices such as microphones to the input of amplifiers.
Mainly consists of two coils or windings placed on a common core.
With the increase in size (capacity) and operating voltage, it also needs other parts such as a suitable tank, bushing, conservator, breather, etc.
Two basic parts—core and windings will be discussed.
Transformer Core:
composition depends on voltage, current and frequency
core materials are soft iron and steel
Air-core transformers are used when the voltage source has a high frequency (above 20 kHz) and Iron-core when frequency is low (below 20 kHz).
constructed of laminated steel to provide a continuous magnetic path
high-grade silicon steel is used where hysteresis loss is very low
alternating flux induced eddy currents in the core.
cause eddy current loss in the core
Silicon content in the steel increases its resistivity to eddy-current loss, thereby reducing eddy-current losses.
To reduce eddy-current losses further, the core is laminated by a light coat of varnish or by an oxide layer on the surface
two main shapes of cores used in laminated steel-core
transformers
Transformer Windings:
Two coils, called windings, are wrapped around a core
primary winding in which electrical energy is fed
secondary winding which is connected to the load
Windings made up of an insulated copper conductor in the form of a round wire or strip
The windings are insulated from each other and the core, using cylinders of insulating material such as a press board or Bakelite
For simplicity, the primary and secondary windings are shown on separate limbs of the core.
If such an arrangement is used in actual practice, all the flux produced in the primary winding will not link with the secondary winding.
Some of the flux will leak out through the air known as leakage flux
leakage flux cause poor performance of the transformer.
Hence, to reduce leakage flux, the windings are placed together on the same limb in actual transformers
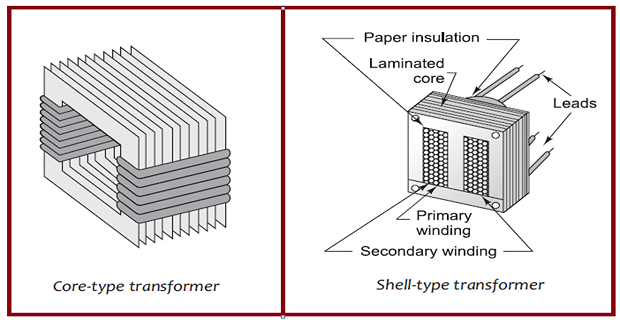
| Core-type | Shell-type | |
|---|---|---|
| 1. | magnetic frame with two limbs. | magnetic frame with three limbs. |
| 2. | single magnetic circuit | two magnetic circuits |
| 3. | winding encircles the core | core encircles most part of winding |
| 4. | cylindrical windings | sandwich-type windings |
| 5. | easy to repair | not easy to repair |
| 6. | better cooling as windings are uniformly distributed on two limbs | ineffective cooling as the windings are surrounded by the core |
| 7. | low-voltage transformers | high-voltage transformers |
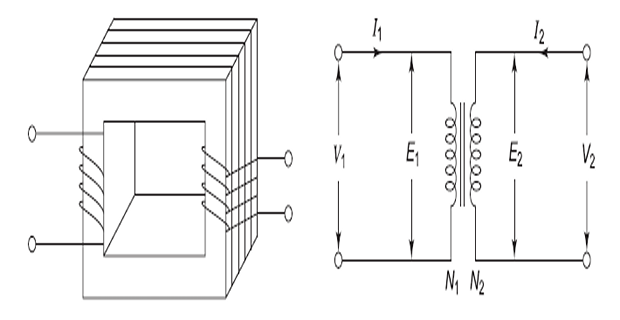
When an alternating voltage \(V_1\) is applied to a primary winding, an alternating current \(I_1\) flows in it producing an alternating flux in the core.
As per Faraday’s laws of electromagnetic induction, an emf \(e_1\) is induced in the primary winding. \[e_{1}=-N_{1}{\frac{d\phi}{d t}}\]
Assuming leakage flux to be negligible, almost the whole flux produced in the primary winding links with the secondary winding.
Hence, an emf \(e_2\) is induced in the secondary winding. \[e_{2}=-N_{2}{\frac{d\phi}{d t}}\]
Thus, energy transfer from primary to secondary winding
If \(N_2>N_1~\Rightarrow\) step-up transformer
If \(N_2<N_1~\Rightarrow\) called a step-down transformer
step-up transformer increase the voltage at the output, whereas a step-down transformer is used to decrease the voltage at the output.
Primary winding \(\Rightarrow\) sinusoidal alternating voltage \(\Rightarrow\) alternating current flows in the winding \(\Rightarrow\) sinusoidally varying flux in the core \[\phi = \phi_m\sin\omega t\]
As per Faraday’s laws of electromagnetic induction, an emf \(e_1\) is induced in the primary winding. \[\begin{aligned} e_1& =-N_{1}\frac{d\phi}{d t} \\ &=-N_1\frac{d}{dt}(\phi_m\sin\omega t) \\ &=-N_1\phi_m\omega\cos\omega t \\ &=N_1\phi_m\omega\sin{(\omega t-90^{\circ})} \\ &=2\pi f\phi_m N_1\sin{(\omega t-90^{\circ})} \end{aligned}\]
Maximum value of induced emf \(=2\pi f\phi_m N_1\)
RMS value of induced emf in primary winding \[E_1=\frac{E_{\max}}{\sqrt{2}}=\boxed{\frac{2\pi f\phi_mN_1}{\sqrt{2}}=4.44f\phi_m N_1}\]
RMS value of induced emf in the secondary winding \[\begin{aligned} &\boxed{E_2 =4.44f\phi_m N_2 } \\ \text{Note:}~ \Rightarrow~&\boxed{\frac{E_{1}}{N_{1}} =\frac{E_2}{N_2}=4.44f\phi_m } \end{aligned}\]
Thus, emf per turn is same in primary and secondary windings
Also equal emf is induced in each turn of the primary and secondary windings.
\[\begin{aligned} E_1& =4.44f\phi_m N_1 \qquad E_2 =4.44f\phi_m N_2 \\ \frac{E_{2}}{E_{1}}& =\frac{N_2}{N_1}=K ~~ \Leftarrow~{\color{magenta}{\textbf{Transformation ratio}}} \end{aligned}\]
\[\begin{aligned} & {\color{red}{\textbf{Neglecting losses}}}\\ V_1& \approx E_1 \quad V_2 \approx E_2 \\ \frac{E_{2}}{E_{1}}& =\frac{V_2}{V_1}=\frac{N_2}{N_1}=K\\ V_1I_1 & = V_2I_2\\ {\frac{I_{1}}{I_{2}}}&={\frac{V_{2}}{V_{1}}}=K\\ \end{aligned}\]
\[\begin{aligned} N_2 & > N_1 \quad \Rightarrow~K>1 \Rightarrow~{\color{teal}{\textbf{Step-up}}} \\ N_2 & < N_1 \quad \Rightarrow~K<1\Rightarrow~{\color{brown}{\textbf{Step-down}}} \end{aligned}\]
\[\frac{E_{2}}{E_{1}} =\frac{V_2}{V_1}={\frac{I_{1}}{I_{2}}}=\frac{N_2}{N_1}=K\]
The rating of a transformer indicates the output power from it.
Load is not fixed and power factor continuously changes.
Rating is not expressed in terms of power but in terms of the product of voltage and current, known as the VA rating.
Rating is generally expressed in kilovolt-ampere (kVA). \[\text{kVA rating of a transformer} = \frac{V_{1}I_{1}}{1000}=\frac{V_{2}I_{2}}{1000}\]
We can calculate full-load currents of primary and secondary windings from kVA rating of a transformer.
Full-load current is the maximum current which can flow through the winding without damaging it. \[\begin{aligned} \text{Full-load primary current}~ I_1 & =\frac{\mathrm{kVA rating}\times1000}{V_1}\\ \text{Full-load secondary current}~ I_2 & =\frac{\mathrm{kVA~rating}\times1000}{V_2} \end{aligned}\]