Electrical Sciences · Lecture

OC & SC Tests on Transformer

Transformers

Prof. Mithun Mondal BITS Pilani, Hyderabad Campus
SECTION 01

Demonstrative Video

SECTION 02

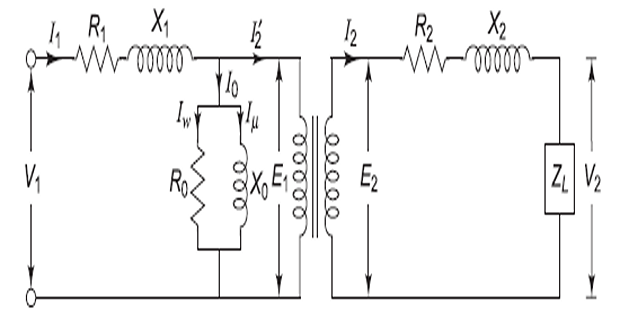
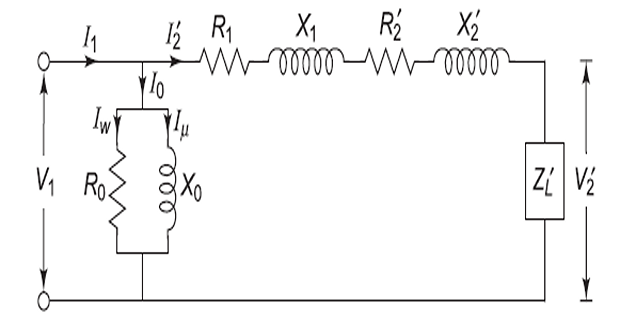
Equivalent Circuit

  • Practical transformer excluding no-load current:

    • \(R_i\) and \(X_i\) represents resistance and leakage reactance

  • Practical transformer including no-load current components:

    • \(I_1 = I_0 + I_2^{\prime}\)

image

  • Modified Circuit of Primary Winding:

\[\begin{aligned} I_1^2R_2'& =I_2^2R_2 ~ \Leftarrow~\text{same power loss} \\ \Rightarrow~R_2'& =\left(\frac{I_2}{I_1}\right)^2R_2=\frac{R_2}{K^2} \\ &\\ &\boxed{R_2' = \frac{R_2}{K^2}} ~\qquad ~\boxed{X_2' = \frac{X_2}{K^2}} \end{aligned}\]

  • Note: Since all quantities are transferred to primary, the transformer need not be shown

  • As \(I_0\) is very small as compared to \(I_1~\Rightarrow\) drop across \(R_1\) and \(X_1\) due to \(I_0\) can be neglected \(\Rightarrow\) shift no-load components to the extreme left

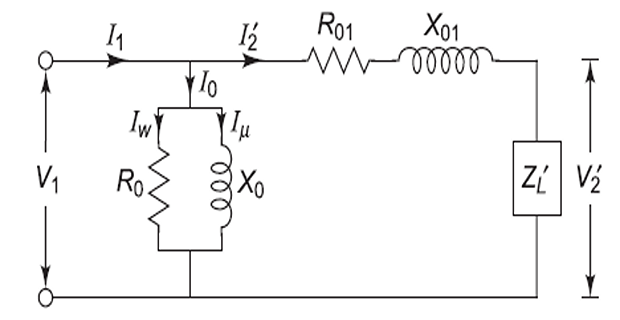
image
Equivalent parameters referred to primary:

\[\begin{aligned} R_{01} & =R_1+R_2'=R_1+\dfrac{R_2}{K^2} \\ X_{01} & =X_1+X_2'=X_1+\dfrac{X_2}{K^2} \\ Z_{01} & =\sqrt{R_{01}^2+X_{01}^2} \end{aligned}\]
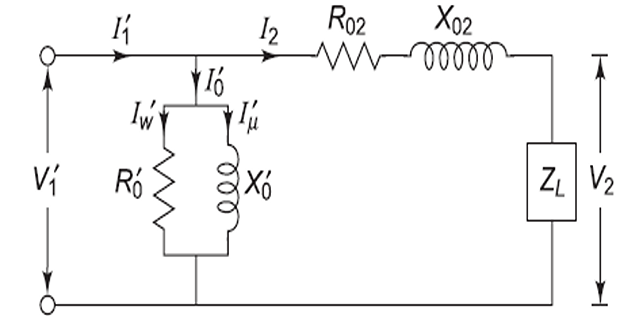
image

Equivalent parameters referred to secondary:

image

\[\begin{aligned} R_{02} & =R_2+R_1'=R_2+K^2 \cdot R_1 \\ X_{02} & =X_2+X_1'=X_2+ K^2 \cdot X_1 \\ Z_{02} & =\sqrt{R_{02}^2+X_{02}^2} = K^2 \cdot Z_{01} \end{aligned}\]

Remember

  • Shifting primary R/X to the secondary, multiply it by \(K^2\)

  • Shifting secondary R/X to the primary, divide it \(K^2\)

SECTION 03

Voltage Regulation

  • Transformer loaded, \(V_2~\downarrow\) due to a drop across \(R_2\) and \(X_2\) .

  • \[\begin{aligned} \text{Regulation} & =\frac{\left(\begin{matrix}\text{Secondary terminal}\\ \text{voltage on no load}\end{matrix}\right)-\left(\begin{matrix}\text{Secondary terminal}\\ \text{voltage on full load}\end{matrix}\right)}{\text{Secondary terminal voltage on no load}}\\ & = \dfrac{E_2-V_2}{E_2} \\ \text{%Regulation} & = \dfrac{E_2-V_2}{E_2} \times 100 \end{aligned}\]
    . from no load to full load conditions, expressed as a fraction of the no-load secondary voltage is called Change in
\[\begin{aligned} \text{Total voltage drop} & =E_2-V_2\\ &=O C-O A\\ &=O M-O A\\ &=A M=A N+N M\\ \end{aligned}\]
\[\begin{aligned} \text { Approximate voltage drop } & \approx A N \quad(\because N M \text { is very small) } \\ & =A D+D N \\ & =A D+B L \\ & =I_2 R_{02} \cos \phi+I_2 X_{02} \sin \phi \\ \% \text { regulation } & =\frac{I_2 R_{02} \cos \phi+I_2 X_{02} \sin \phi}{E_2} \times 100 \end{aligned}\]
For leading pf, Approximate voltage drop
\[\begin{aligned} &\boxed{\% \text { regulation } =\frac{I_2 R_{02} \cos \phi \pm I_2 X_{02} \sin \phi}{E_2} \times 100}\\ + &~~ \text{lagging pf} \qquad - ~~ \text{leading pf} \end{aligned}\]
\[\begin{aligned} \% {\color{red}{\textbf{regulation}}} & =\frac{I_1 R_{01} \cos \phi \pm I_1 X_{01} \sin \phi}{V_1} \times 100 \quad \Leftarrow~\text{primary side}\\ & \\ \% \text { regulation } & =\frac{100 I_2 R_{02}}{E_2} \cos \phi \pm \frac{100 I_2 X_{02}}{E_2} \sin \phi \\ & =\boxed{v_r \cos \phi \pm v_x \sin \phi }\\ &\boxed{v_r =\frac{ I_2 R_{02}}{E_2}\times 100}= {\color{magenta}{\textbf{percentage resistive drop }}}\\ & \boxed{v_x =\frac{I_2 X_{02}}{E_2}\times 100}= {\color{blue}{\textbf{percentage reactive drop }}} \end{aligned}\]
SECTION 04

Efficiency

\[\begin{aligned} \eta & =\dfrac{\mbox{output power}}{\mbox{input power}}\\ &=\dfrac{\mbox{output power}}{\mbox{output power+losses}}\\ & =\dfrac{\mbox{output power}}{\mbox{output power+iron losses+copper losses}}\\ & \boxed{=\dfrac{V_{2}I_{2}\cos\Phi_{2}}{V_{2}I_{2}\cos\Phi_{2}+P_{i}+P_{c}}} \end{aligned}\]
where

If \(x\) is the fraction of the full-load, then efficiency is given as

\[\begin{aligned} \eta_{x} & =\boxed{\dfrac{x\times\mbox{Output}}{x\times\mbox{Output}+P_{i}+x^{2}P_{c}}}\\ &=\boxed{\dfrac{xV_{2}I_{2}\cos\Phi_{2}}{xV_{2}I_{2}\cos\Phi_{2}+P_{i}+x^{2}I_{2}^{2}R_{T}}} \end{aligned}\]

Condition for the maximum efficiency

\[\eta = \dfrac{V_2I_2\cos\Phi_2}{V_2I_2\cos\Phi_2+P_i+I_2^2R_T} = \dfrac{V_2\cos\Phi_2}{V_2\cos\Phi_2+P_i/I_2+I_2R_T}\]

  • \(V_2\) is constant

  • for a given \(\cos\Phi_2\) , \(\eta\) depends upon \(I_2\)

  • \[\begin{aligned} \dfrac{d}{dI_{2}} & =\left(V_{2}\cos\Phi_{2}+\dfrac{P_{i}}{I_{2}}+I_{2}R_{T}\right)=0\\ & \Rightarrow0-\dfrac{P_{i}}{I_{2}^{2}}+R_{T}=0\\ & \Rightarrow P_{i}=I_{2}^{2}R_{T}\\ & \boxed{\Rightarrow\mbox{Iron loss}=\mbox{copper loss}} \end{aligned}\]
    efficiency will be maximum when
\[I_2 = \sqrt{\dfrac{P_i}{R_T}}\]
For maximum efficiency . Then is the fraction of full load KVA at which If Value of output current for maximum efficiency
SECTION 05

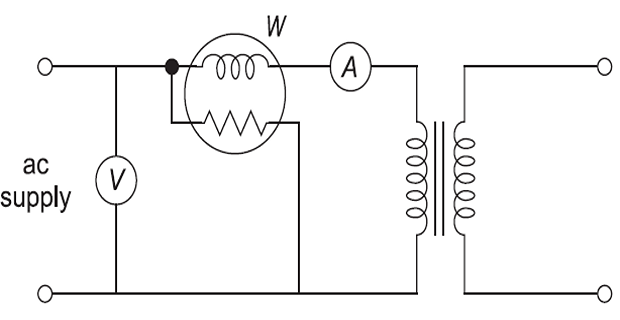
OC & SC Tests

Open-Circuit Test (OC)

  • Purpose : To determine

    1. iron loss or core loss ( \(W_i\) )

    2. magnetising resistance ( \(R_0\) )

    3. magnetising reactance ( \(X_0\) )

  • Test Connections :

    • HV open and supply and meters are connected to LV side

    • ammeter indicates no-load current (3-5% of F.L current)

    • Cu losses negligible and wattmeter indicates iron loss

    image
\[\begin{aligned} & \text { Wattmeter reading }=W_i \\ & \text { Voltmeter reading }=V_1 \\ & \text { Ammeter reading }=I_0 \\ & W_i=V_1 I_0 \cos \phi_0 \\ & \boxed{\cos \phi_0=\frac{W_i}{V_1 I_0}} \\ & \boxed{I_w=I_0 \cos \phi_0} \qquad \boxed{I_\mu=I_0 \sin \phi_0} \\ & \boxed{R_0=\frac{V_1}{I_w}}\\ & \boxed{X_0=\frac{V_1}{I_\mu}} \\ & \end{aligned}\]
Calculation:

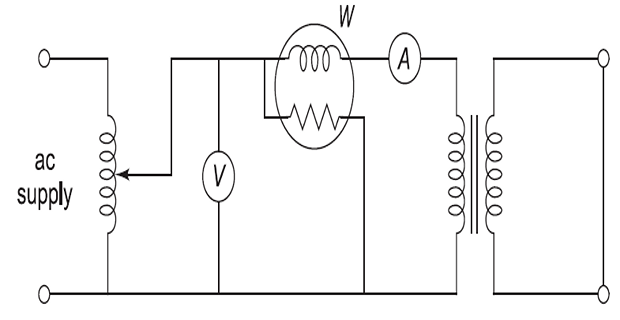
Short-Cicuit Test (SC)

  • Purpose : To determine

    1. full-load copper loss

    2. equivalent resistance ( \(R_{01}\) or \(R_{02}\) )

    3. equivalent reactance ( \(X_{01}\) or \(X_{02}\) )

  • Test Connections :

    • LV side short-circuited while low-voltage is applied to other winding

    • Applied voltage slowly increased until F.L. current flows in the winding

    • Normally, the applied voltage is 5 to 10% of the rated voltage

    • Flux produced in core small & iron losses are very small.

    • Thus, wattmeter indicates full-load copper loss.

    image
\[\begin{aligned} & \text { Wattmeter reading }=W_{\mathrm{sc}} \\ & \text { Voltmeter reading }=V_{\mathrm{sc}} \\ & \text { Ammeter reading }=I_{\mathrm{sc}} \\ &\\ &\boxed{ Z_{sc}=\frac{V_{\mathrm{sc}}}{I_{\mathrm{sc}}}} \\ & \boxed{R_{sc}=\frac{W_{\mathrm{sc}}}{I_{\mathrm{sc}}^2}} \\ & \boxed{X_{sc}=\sqrt{\left(Z_{sc}\right)^2-\left(R_{sc}\right)^2}} \end{aligned}\]