Demonstrative Video
Basic Electronics Contents:
Semiconductors
PN Junction Diode
Bipolar Junction Transistors (BJT)
Semiconductor Fundamentals
Semiconductor Materials
Semiconductor: are special class of elements having a conductivity between that of a good conductor and that of an insulator
Semiconductor materials fall into one of two classes:
Single crystal - germanium (Ge) and silicon (Si) having repetitive crystal structure
Compound - gallium arsenide (GaAs), cadmium sulphide (CdS), gallium nitride (GaN), and gallium arsenide phosphide (GaAsP) are constructed of two or more semiconductor materials of different atomic structure.
The three semiconductors used most frequently in the construction of electronic device are Ge, Si, and GaAs.
Best conductors (silver, copper, and gold) have one valence electron, whereas the best insulators have eight valence electrons
Best semiconductors have four valence electrons.
Many years ago, Ge was only material suitable for making semiconductor devices.
But Ge devices had a fatal flaw (their excessive reverse current, discussed later) that engineers could not overcome.
Next to oxygen, silicon is the most abundant element on the earth.
The advantages of Si immediately made it the semiconductor of choice.
Without it, modern electronics, communications, and computers would be impossible.
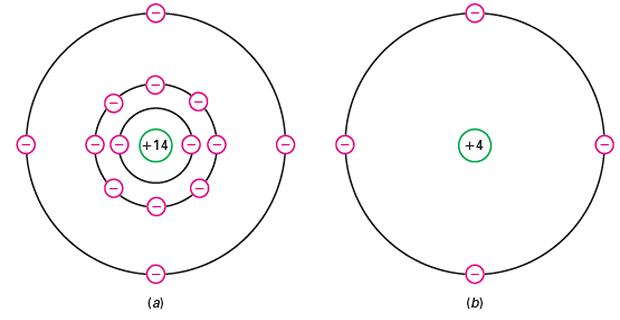
An isolated silicon atom has 14 protons and 14 electrons
core net charge 14 because it contains 14 protons in the nucleus and 10 electrons in the first two orbits.
Energy Band
The range of energies possessed by electrons of the same orbit in a solid is known as energy band.
In a single isolated atom, electrons revolving in any orbit possess a definite energy.
However in a solid, an atom is greatly influenced by the closely packed neighbouring atoms.
Because of this the electrons in the same orbit have a range of energies rather than a single energy.
Although there are number of energy bands in solids, but we are more concerned with the following:
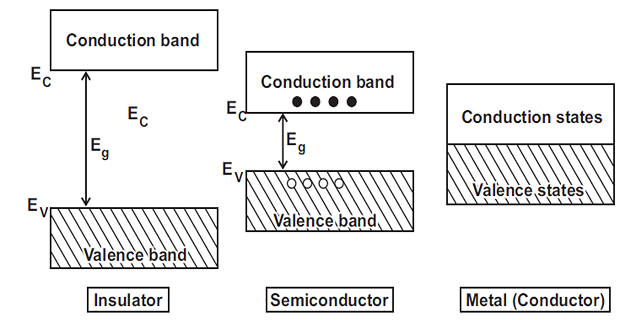
Valence band: Outermost orbit electrons in an atom, highest energy level.
Conduction band: Loose electrons responsible for current conduction.
Forbidden Energy Gap: Gap between valence and conduction bands.
Silicon Crystal Structure:
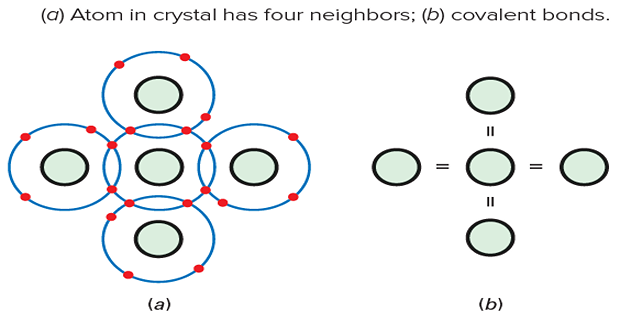
Silicon atoms arrange themselves in an orderly pattern called a crystal.
Each silicon atom shares its electrons with four neighbouring atoms.
This sharing allows each atom to have a total of eight electrons in its valence orbit.
Covalent bonds form between atoms due to the equal and opposite forces of attraction.
Billions of covalent bonds hold the silicon crystal together, giving it solidity.
Eight Electrons and Chemical Stability:
Each atom in a silicon crystal has eight electrons in its valence orbit.
This configuration results in chemical stability and solid material.
Elements tend to combine and share electrons to achieve eight electrons in their outer orbit.
The reason why eight electrons provide stability is not fully understood, but it is observed in various materials.
Scientific Laws and Explanations:
There are advanced physics equations that partially explain the stability of eight electrons in different materials.
The significance of the number eight remains unexplained, similar to other observed laws in physics, such as the law of gravity and Coulomb’s law.
When the valence orbit has eight electrons, it is saturated because no more electrons can fit into this orbit
Ambient Temperature and Vibrating Atoms:
Ambient temperature is the temperature of the surrounding air.
At temperatures above absolute zero (\(-273^{\circ}\)), the heat energy causes the atoms in a silicon crystal to vibrate.
Higher ambient temperatures result in stronger mechanical vibrations.
The warmth felt when picking up a warm object is due to the vibrating atoms.
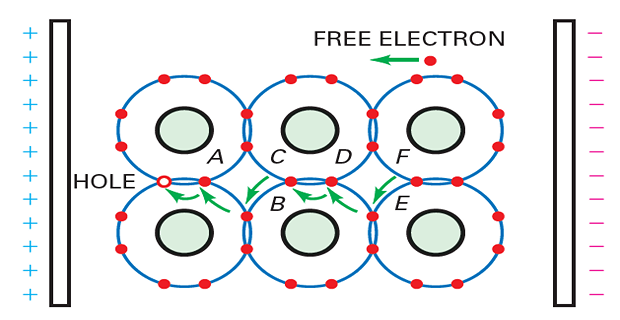
Generation of Free Electrons and Holes:
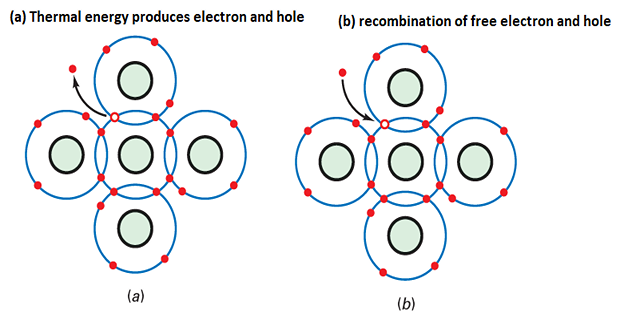
Vibrations in a silicon crystal can dislodge electrons from the valence orbit.
The released electron gains enough energy to move into a larger orbit, becoming a free electron.
The departure of the electron creates a vacancy in the valence orbit called a hole.
Holes behave like positive charges and can attract and capture nearby electrons.
The presence of holes is a critical difference between conductors and semiconductors.
Role of Doping:
At room temperature, thermal energy produces only a few holes and free electrons.
To increase the number of holes and free electrons, the crystal needs to be doped.
Recombination and Lifetime:
In a pure silicon crystal, thermal energy generates an equal number of free electrons and holes.
Free electrons move randomly throughout the crystal.
Occasionally, a free electron and a hole come close to each other, resulting in recombination.
Recombination is the merging of a free electron and a hole.
The time between the creation and disappearance of a free electron is called the lifetime.
The lifetime can vary from a few nanoseconds to several microseconds, depending on the crystal’s quality and other factors.
Main Points inside a Silicon Crystal:
Creation of Free Electrons and Holes:
Thermal energy generates some free electrons and holes.
Recombination of Free Electrons and Holes:
Other free electrons and holes recombine.
Temporary Existence of Free Electrons and Holes:
Some free electrons and holes exist temporarily, waiting for recombination.
Intrinsic Semiconductor
An extremely pure semiconductor is called an intrinsic semiconductor.
At absolute zero temperature, the valence band of an intrinsic semiconductor is completely filled, and the conduction band is completely empty.
When heat energy is supplied (e.g., at room temperature), some valence electrons are lifted to the conduction band, creating free-moving electrons and holes.
Intrinsic semiconductors have a negative temperature coefficient of resistance, meaning their resistivity decreases and conductivity increases with a rise in temperature.
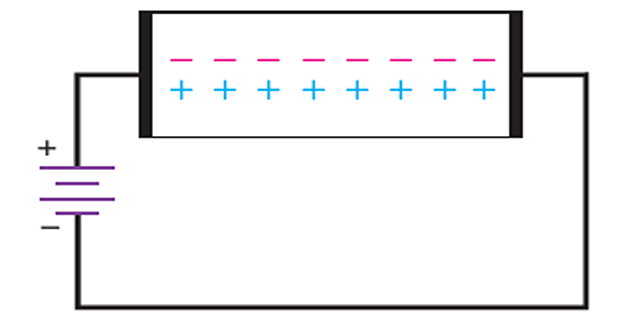
Extrinsic Semiconductor
Extrinsic Semiconductor:
An intrinsic semiconductor, on its own, is not useful for electronic devices.
To make it conductive, a small amount of suitable impurity is added, resulting in an extrinsic (impure) semiconductor.
The process of adding impurities to a semiconductor is called doping, which needs to be closely controlled.
Extrinsic semiconductors are classified based on the type of impurity added:
n-type semiconductor: When a donor impurity is added, creating excess free electrons.
p-type semiconductor: When an acceptor impurity is added, creating excess holes.
Hole flow through a semiconductor
n-type semiconductors
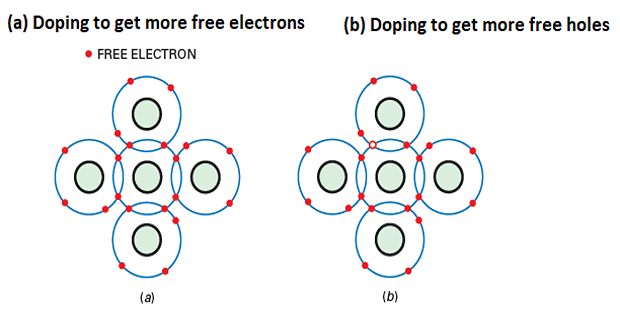
When a small amount of pentavalent impurity is added to a pure semiconductor, it creates an extrinsic semiconductor known as an n-type semiconductor.
Pentavalent impurities such as arsenic and antimony provide a large number of free electrons in the semiconductor crystal.
These impurities are called donor impurities because each atom donates one free electron to the semiconductor crystal.
The pentavalent impurity atoms fit into the crystal structure, with their four valence electrons forming covalent bonds and the fifth electron being free.
The small amount of pentavalent impurity results in a large number of free electrons available for conduction.
p-type semiconductors
When a small amount of trivalent impurity is added to a pure semiconductor, it creates an extrinsic semiconductor known as a p-type semiconductor.
Trivalent impurities such as boron, gallium and indium provide a large number of free holes in the semiconductor crystal.
These impurities are called acceptor impurities because each atom creates a hole that can accept an electron from the semiconductor crystal.
The trivalent impurity atoms fit into the crystal structure, with their three valence electrons forming covalent bonds but leaving one covalent bond incomplete, creating a hole.
The small amount of trivalent impurity results in a large number of holes available in the semiconductor.
Summary
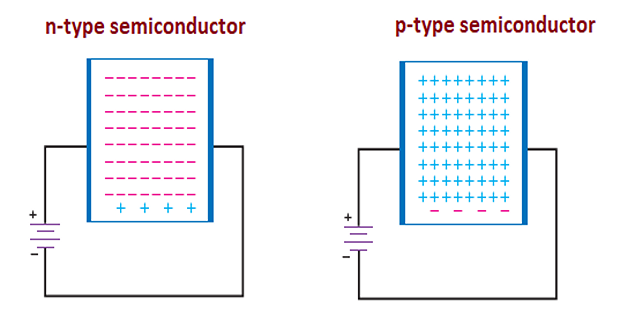
In an n-type semiconductor, a small amount of pentavalent impurity is added, providing a large number of free electrons. These impurities are donor impurities.
In a p-type semiconductor, a small amount of trivalent impurity is added, providing a large number of free holes. These impurities are acceptor impurities.
Mass Action Law
Under thermal equilibrium, the product of the number of holes and electrons is constant and independent of the amount of donor and acceptor impurity doping.
\[\boxed{n \cdot p = n_i^2}\]While considering the conductivity of the doped semiconductors, only the dominant majority charge carriers have to be considered
Charge densities in doped semiconductors
N-type semiconductor:
\[\begin{aligned} N_D & = \text{conc. of donor atoms} \\ n_N & = \text{electron conc. in N-type} \\ p_N & = \text{hole conc. in N-type} \end{aligned}\]
P-type semiconductor:
\[\begin{aligned} p_P & = N_A + n_P \approx N_A \\ n_p & = \dfrac{n_i^2}{p_P}~(\text{from mass action law})\\ & \approx \dfrac{n_i^2}{N_A} \end{aligned}\]\[\begin{aligned} N_A & = \text{conc. of acceptor atoms} \\ p_p & = \text{hole conc. in P-type} \\ n_P & = \text{electron conc. in P-type} \end{aligned}\]
Extrinsic Conductivity
- \[\sigma_N = qn_N\mu_n \approx qN_D\mu_n \quad \text{since}~n_N \approx N_D\]Conductivity of N-type semiconductor:
- \[\sigma_P= qn_P\mu_p \approx qN_A\mu_p \quad \text{since}~p_P \approx N_A\]Conductivity of P-type semiconductor:
If conc. of donor atoms added to a P-type semiconductor exceeds the conc. of acceptor atoms i.e. \(N_D >> N_A\) then P-type is converted to N-type
Similarly, if \(N_A >> N_D\), N-type converted to P-type
Problem
Find the conductivity of silicon
in intrinsic condition at a room temp. of \(300^{\circ}\)K
with donor impurity of 1 in \(10^8\)
with acceptor impurity of 1 in \(5\times 10^{7}\)
with both impurities present simultaneously
Given that
Solution
- \[\begin{aligned} \sigma_i &=q n_i\left(\mu_n+\mu_p\right) =\left(1.6 \times 10^{-19}\right)\left(1.5 \times 10^{10}\right)(1300+500) \\ &=4.32 \times 10^{-6} \mathrm{~S} / \mathrm{cm} \end{aligned}\]In intrinsic condition,
- \[\begin{aligned} p &=\frac{n_i^2}{n} \approx \frac{n_i^2}{N_D} =\frac{\left(1.5 \times 10^{10}\right)^2}{5 \times 10^{14}}=0.46 \times 10^6 \mathrm{~cm}^{-3} \end{aligned}\]\[\begin{aligned} \sigma &=n q \mu_n=N_D q \mu_n \\ &=\left(5 \times 10^{14}\right)\left(1.6 \times 10^{-19}\right)(1300) \\ &=0.104 \mathrm{~S} / \mathrm{cm} . \end{aligned}\]\(p\)\(p \ll n\) Therefore, Further, Hence, Number of silicon atoms
Drift and Diffusion Currents
Flow of charge (current) through a semiconductor or PN junction diode has two components:
Drift current
Diffusion current
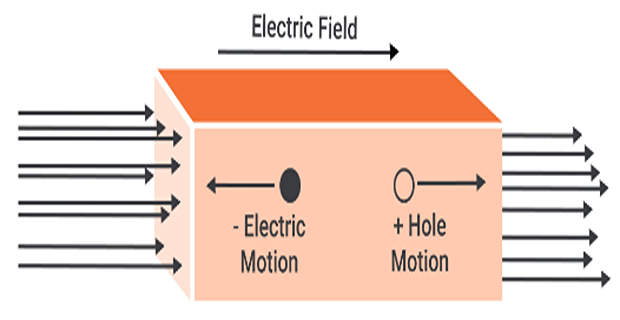
Drift current:
Drift current arises from the movement of carriers in response to an applied electric field.
Positive carriers (holes) move in the same direction as the electric field
Negative carriers (electrons) move in the opposite direction.
The net motion of charged particles generates a drift current that is in the same direction as the applied electric field.
Diffusion current :
Electric current can flow even in the absence of applied voltage provided a concentration gradient exists
When the number of either electrons or holes is greater in one region than that of other region
Charge carrier move from higher to lower concentration of same type of charge carrier
Movement of charge carrier resulting in a current called diffusion current
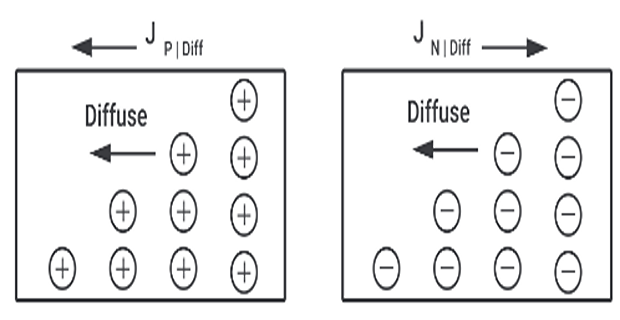
hole density \(p(x)\) decreases with increasing \(x\), hence negative sign
\(J_p\) is positive in \(+x\) direction
\(dn/dx\) and \(dp/dx\) are concentration gradients
\(D_n\) and \(D_p\) are diffusion coefficients in cm2/s
- \[= \begin{cases} J_p=q p \mu_p E-q D_p \dfrac{\mathrm{d} p}{\mathrm{~d} x} \\ \\ J_n=q n \mu_n E-q D_n \dfrac{\mathrm{d} n}{\mathrm{~d} x} \end{cases}\]Total current :
Einstein Relationship :
Relationship between mobility and diffusion coefficient of a particular type of charge carrier in the same semiconductor
Higher the charge carrier mobility, greater will be its tendency to diffuse
Used to determine \(D_{p,n}\) by experimentally measuring \(\mu_{p,n}\)
Problem-1
A p-type semiconductor with a length of 5 cm, cross-sectional area of 1 cm2, and a doping concentration of \(1 \times 10^{16} \, \text{cm}^{-3}\) is subjected to an electric field of 100 V/m. Calculate the drift current in the semiconductor.
Solution:
Problem-2
A silicon bar with a length of 2 mm and a cross-sectional area of \(0.2 \, \text{mm}^2\) has an excess minority carrier concentration of \(3 \times 10^{14} \, \text{cm}^{-3}\). The diffusion coefficient for minority carriers in silicon is \(10^{-9} \, \text{m}^2/\text{s}\). Calculate the diffusion current across the silicon bar.
Solution:
Given Data: