Number Systems & Conversions

Introduction to Number Systems

What is a Number System?

Definition

A number system is a mathematical notation for representing numbers using a consistent set of digits or symbols.

Key Components:

  • Base (Radix): Number of unique digits

  • Digits: Symbols used for representation

  • Positional Value: Weight of each position

  • Place Value: Base raised to position power

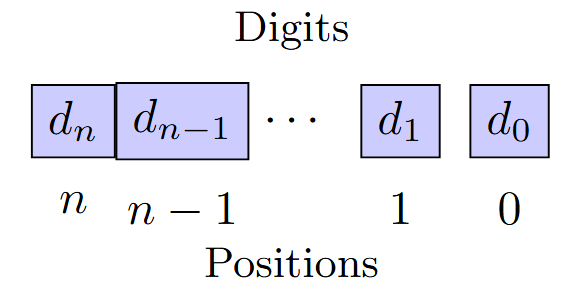
Position of the digits
Position of the digits

General Formula

\(N = d_n \times \text{base}^n + d_{n-1} \times \text{base}^{n-1} + \cdots + d_1 \times \text{base}^1 + d_0 \times \text{base}^0\)

Common Number Systems

The Four Essential Number Systems

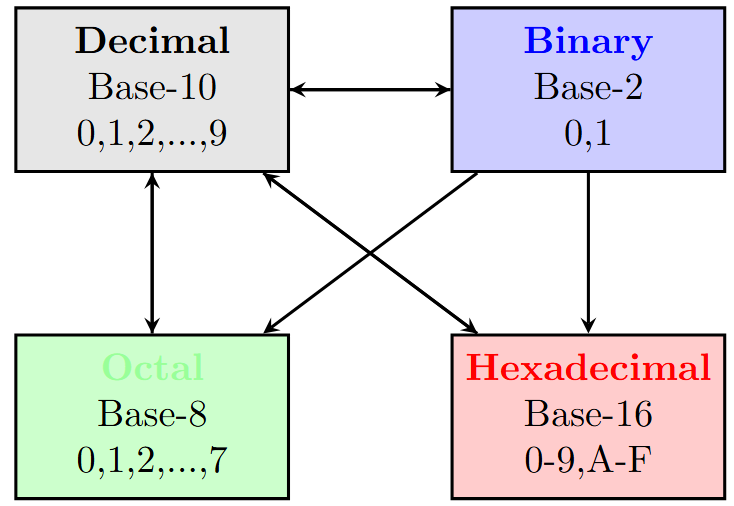
The four essential number system
The four essential number system

Decimal Number System (Base-10)

Characteristics:

  • Base: 10

  • Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

  • Most familiar to humans

  • Natural counting system

Example: \(1234_{10}\)

\[\begin{aligned} 1234_{10} &= 1 \times 10^3 + 2 \times 10^2 \\ &\quad + 3 \times 10^1 + 4 \times 10^0 \\ &= 1000 + 200 + 30 + 4 \\ &= 1234_{10} \end{aligned}\]

The position weights in base-10 system
The position weights in base-10 system

Binary Number System (Base-2)

Characteristics:

  • Base: 2

  • Digits: 0, 1 only

  • Foundation of digital systems

  • Each bit represents ON/OFF state

Example: \(1011_2\)

\[\begin{aligned} 1011_2 &= 1 \times 2^3 + 0 \times 2^2 \\ &\quad + 1 \times 2^1 + 1 \times 2^0 \\ &= 8 + 0 + 2 + 1 \\ &= 11_{10} \end{aligned}\]

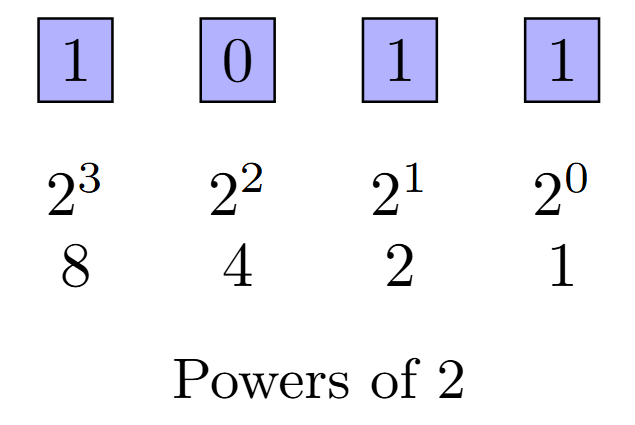
The position powers in binary system
The position powers in binary system

Octal Number System (Base-8)

Characteristics:

  • Base: 8

  • Digits: 0, 1, 2, 3, 4, 5, 6, 7

  • Compact binary representation

  • Historical importance in computing

Example: \(175_8\)

\[\begin{aligned} 175_8 &= 1 \times 8^2 + 7 \times 8^1 + 5 \times 8^0 \\ &= 64 + 56 + 5 \\ &= 125_{10} \end{aligned}\]

The position powers in octal number system
The position powers in octal number system

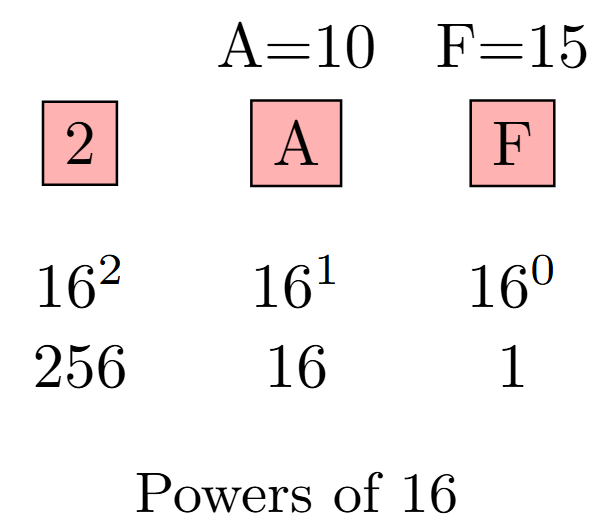
Hexadecimal Number System (Base-16)

Characteristics:

  • Base: 16

  • Digits: 0-9, A-F

  • A=10, B=11, C=12, D=13, E=14, F=15

  • Widely used in programming

Example: \(2AF_{16}\)

\[\begin{aligned} 2AF_{16} &= 2 \times 16^2 + A \times 16^1 + F \times 16^0 \\ &= 2 \times 256 + 10 \times 16 + 15 \times 1 \\ &= 512 + 160 + 15 \\ &= 687_{10} \end{aligned}\]

The position weights in hexadecimal number system
The position weights in hexadecimal number system

Number System Conversions

Conversion Methods Overview

Base conversion technique overview
Base conversion technique overview

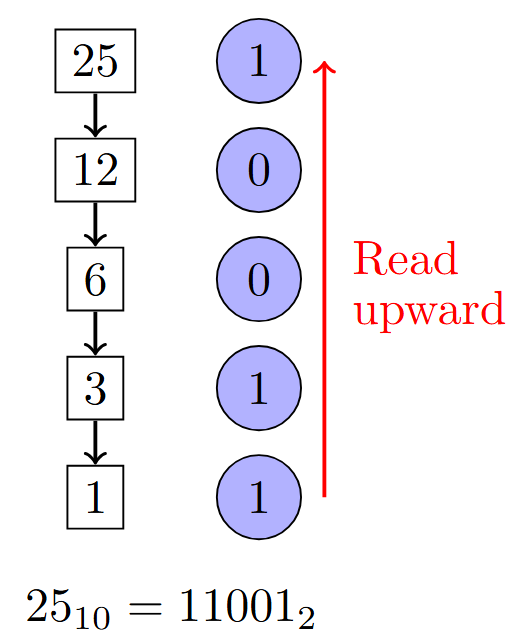
Decimal to Binary Conversion

Method: Successive Division by 2

Example: Convert \(25_{10}\) to Binary

Division Quotient Remainder
\(25 \div 2\) \(12\) \(\mathbf{1}\)
\(12 \div 2\) \(6\) \(\mathbf{0}\)
\(6 \div 2\) \(3\) \(\mathbf{0}\)
\(3 \div 2\) \(1\) \(\mathbf{1}\)
\(1 \div 2\) \(0\) \(\mathbf{1}\)

Result: Read remainders upward: \(11001_2\)

Decimal to binary conversion
Decimal to binary conversion

Verification

\(11001_2 = 1 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 16 + 8 + 0 + 0 + 1 = 25_{10}\) \(\checkmark\)

Binary to Decimal Conversion

Method: Weighted Sum (Positional Notation)

Example: Convert \(110101_2\) to Decimal

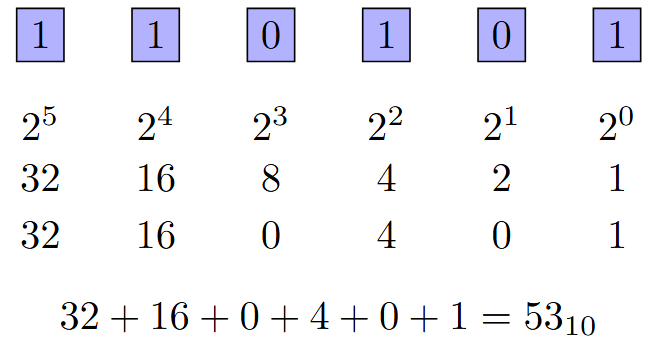
Pro Tip!

For quick mental conversion, memorize powers of 2 up to \(2^{10}\) = 1024

Quick Binary-Octal-Hex Conversions

Key Insight: Direct grouping method for related bases

Binary \(\leftrightarrow\) Octal (Group by 3)

Binary to Octal: Group binary digits in sets of 3 (from right)

Example: \(110101_2\)

Binary to octal conversion
Binary to octal conversion

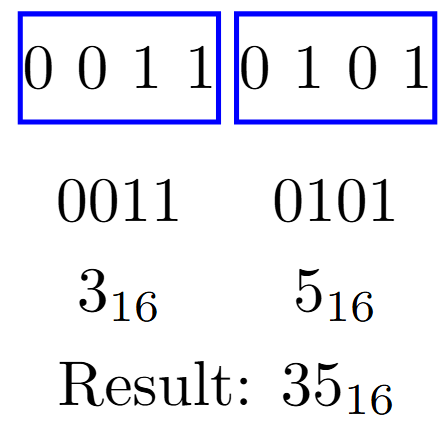
Binary \(\leftrightarrow\) Hex (Group by 4)

Binary to Hex: Group binary digits in sets of 4 (from right)

Example: \(110101_2\)

Binary to hex conversion
Binary to hex conversion

Binary Arithmetic

Binary Addition Rules

Basic Rules

A B Sum Carry
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1

Example 1: Simple Addition

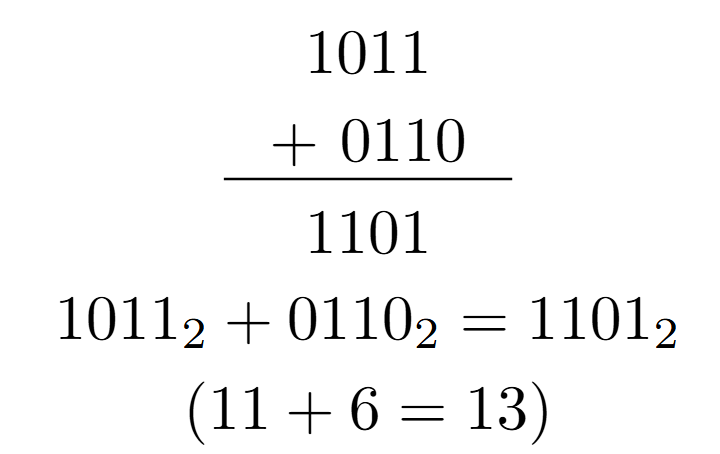
Example 2: With Carry Chain

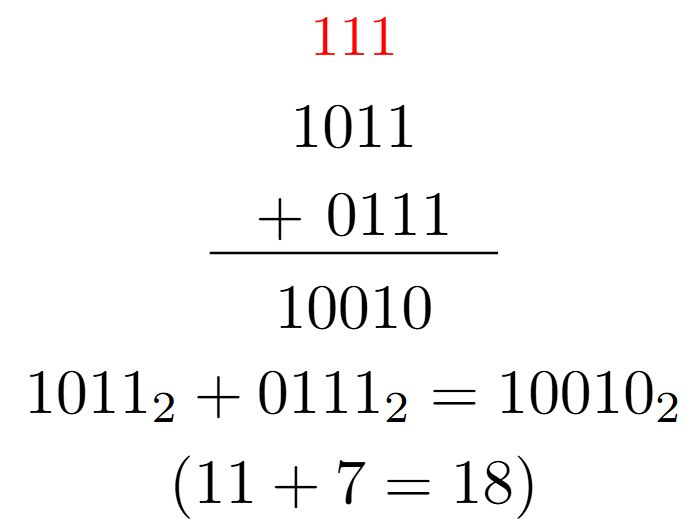
Binary Subtraction Rules

Basic Rules

A B Difference Borrow
0 0 0 0
1 0 1 0
0 1 1 1
1 1 0 0

Example 1: Simple Subtraction

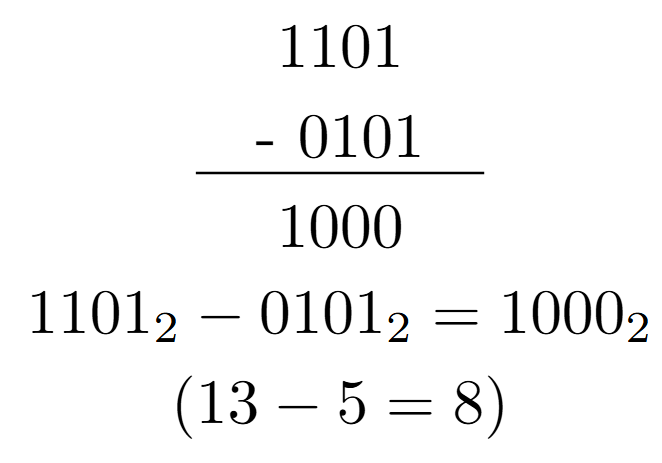
Example 2: With Borrowing

Applications & Summary

Why Different Number Systems Matter

Binary Applications:

  • Digital circuit design

  • Computer programming

  • Data storage & transmission

  • Logic operations

Octal Applications:

  • Unix/Linux file permissions

  • Compact binary representation

  • Assembly programming

Hexadecimal Applications:

  • Memory addressing

  • Color codes (RGB)

  • Machine code representation

  • Debugging tools

Decimal Applications:

  • Human-readable interface

  • Mathematical calculations

  • Financial computations

  • Scientific measurements

Key Takeaway

Each number system serves specific purposes in electronics and computing!

Quick Reference Table

Decimal Binary Octal Hex Notes
0 0000 0 0 -
1 0001 1 1 -
2 0010 2 2 -
3 0011 3 3 -
4 0100 4 4 -
5 0101 5 5 -
6 0110 6 6 -
7 0111 7 7 -
8 1000 10 8 -
9 1001 11 9 -
10 1010 12 A First hex letter
11 1011 13 B -
12 1100 14 C -
13 1101 15 D -
14 1110 16 E -
15 1111 17 F Largest single hex
16 10000 20 10 One hex digit overflow

Summary & Key Points

What We Learned

  • Number Systems: Different bases for representing numbers

  • Conversion Methods: Division method and weighted sum

  • Quick Conversions: Grouping for Binary-Octal-Hex

  • Binary Arithmetic: Addition and subtraction rules

  • Practical Applications: Where each system is used

Practice Problems

  1. Convert \(156_{10}\) to binary, octal, and hexadecimal

  2. Calculate \(1101_2 + 1011_2\) in binary

  3. Convert \(3A7_{16}\) to decimal

  4. Perform \(10110_2 - 01011_2\)

Next Lecture Preview

Boolean Algebra & Logic Gates - The foundation of digital circuits!