Conquering Rectification: Diodes Power Up Electronics

SECTION 01

Overview

Demonstrative Video

Need for a Diode - Initial Thoughts

Charger Circuit Operation

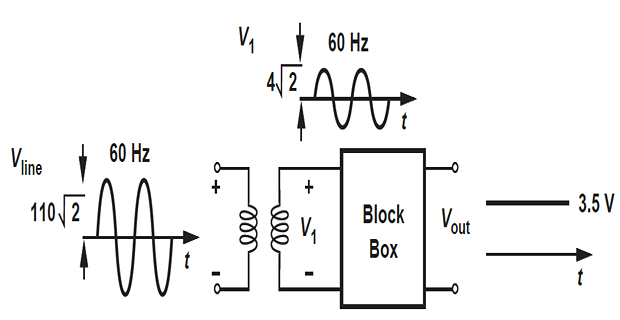
\(\xrightarrow[\text{110 V}]{\text{ac voltage}}\) \(\xrightarrow[\text{4 V}]{\text{Transformer}}\) \(\xrightarrow[\text{3.5 V}]{\text{dc voltage using LPF}}\)
Output of TF using black box exhibits a zero dc content as -ve and +ve half cycles enclose equal areas, leading to a zero average

DIODE - Basic Ideas

Resistor \(\rightarrow\) linear device \(\rightarrow\) current Vs voltage is a straight line.
Diode \(\rightarrow\) nonlinear device \(\rightarrow\) \(I\) Vs \(V\) is not a straight line.
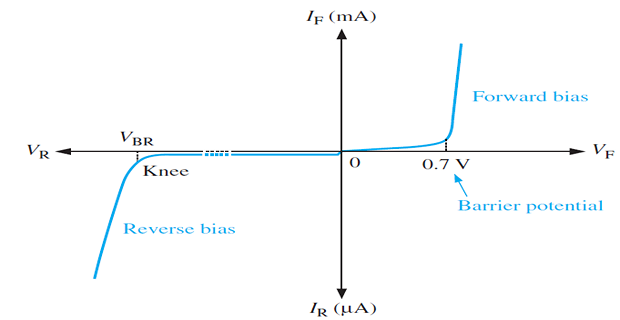
The reason is the barrier potential.
A pn junction is known as a semiconductor diode.
Also known as crystal diodes since grown out of a crystal (like Ge/ Si).

A diode has two terminals.
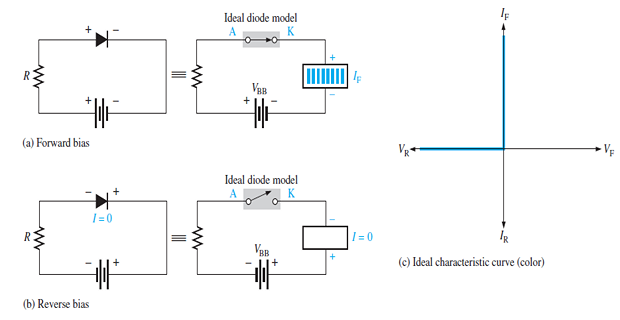
Conducts only when forward biased, i.e., when the terminal connected with the arrowhead is at a higher potential than the terminal connected to the bar.
When reverse biased, practically does not conduct any current through it.

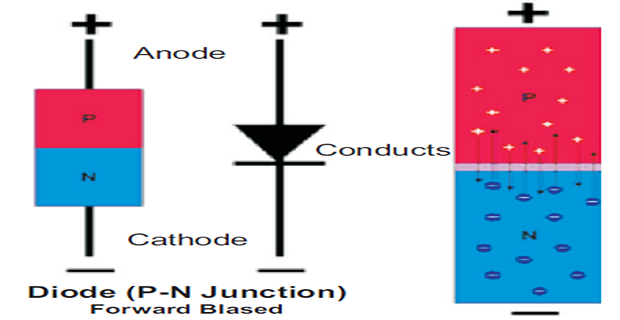
A region around the junction from which the charge carriers (free electrons and holes) are depleted called the depletion layer .
A potential difference built up across the pn junction, which restricts further movement of charge carriers across the junction, known as potential barriers .
When a pn junction is connected across an electric supply (potential difference), the junction is said to be under biasing .

\[\boxed{V_d < V_b \rightarrow I_d \downarrow} \qquad \boxed{V_d > V_b \rightarrow I_d \uparrow}\]

Forward Biasing
- When positive terminal of DC source or battery is connected to the p-type semiconductor and the negative terminal is connected to the n-type semiconductor of a pn junction, the junction is said to be in forward biasing.
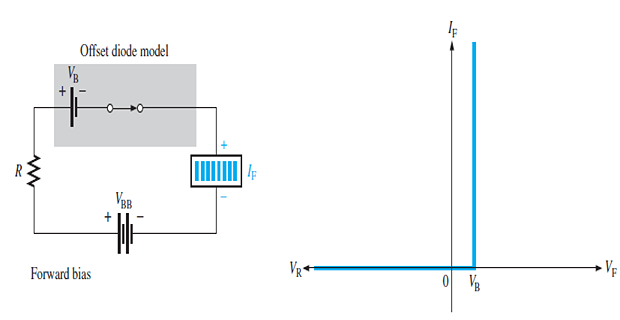
- The junction potential barrier is reduced , and at some forward voltage (0.3 V for Ge and 0.7 V for Si), it is eliminated altogether.
- The junction offers low resistance to the flow of current through it.
- The current magnitude through the circuit depends upon the applied forward voltage.
Reverse Biasing
- When the positive terminal is connected to the n-type semiconductor and the negative terminal is connected to the p-type semiconductor of a pn junction, the junction is said to be in reverse biasing.
- The junction potential barrier is strengthened .
- The junction offers high resistance to the flow of current through it.
- The current magnitude through the circuit depends upon the applied reverse voltage.

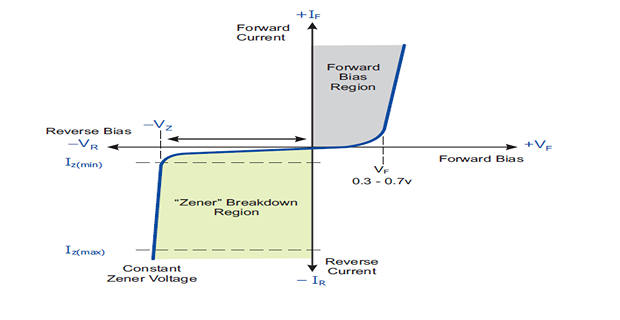
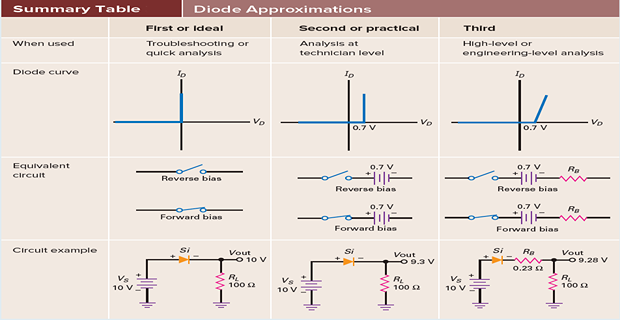
Ideal Diode: acts like a perfect conductor (zero resistance) when forward biased and like a perfect insulator ( \(\infty\) resistance) when reverse biased.

Diode Characteristic Curve

\[\begin{aligned} & V_{\text{anode}} > V_{\text{cathode}} \leftarrow \text{on} \\ & V_{\text{anode}} < V_{\text{cathode}} \leftarrow \text{off} \\ & V_{\text{anode}} - V_{\text{cathode}} = V_D \end{aligned}\]

Real diode

Ideal diode

Si Vs Ge

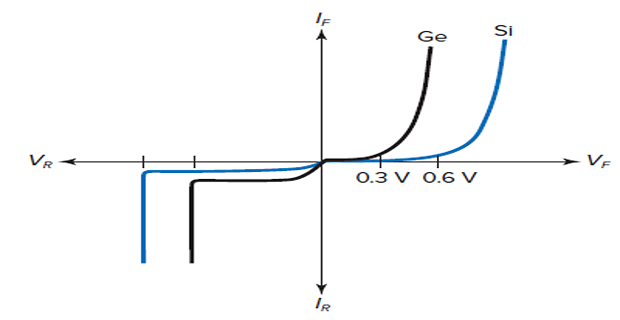
Above the knee voltage, the diode current increases rapidly.
Small increase in the diode voltage cause large increases in diode current.

\[\text{Bulk resistance}~R_B = R_p + R_n\]

. is less than 1 depends on the size of the p and n regions and how heavily doped they are. Often, Bulk Resistance :
Maximum DC Forward Current : If the current in a diode is too large, the excessive heat can destroy the diode. The \(I_{F(max)}\) is one of the maximum ratings given on a data sheet.
\[\begin{aligned} P_D & = V_D \cdot I_D \\ P_{max} & = V_{max} \cdot I_{max} \end{aligned}\]

The power rating is the maximum power the diode can safely dissipate without shortening its life or degrading its properties Power Dissipation :

Diode Current Equation

\[I=I_o\left[\mathrm{e}^{\left(V / \eta V_T\right)}-1\right]\]

\[\begin{aligned} I & = \text{diode current} \\ I_o & = \text{diode reverse saturation current at room temperature}\\ V & = \text{external voltage applied to the diode} \\ \eta &=\text{ a constant, 1 for germanium and 2 for silicon} \\ V_T&=k T / q=T / 11600, \text{volt-equivalent of temperature, i.e., thermal voltage} \\ k & = \text{Boltzmann's constant}~\left(1.38066 \times 10^{-23} \mathrm{~J} / \mathrm{K}\right)\\ q & = \text{charge of the electron}~ \left(1.60219 \times 10^{-19} \mathrm{C}\right)\\ T & = \text{temperature of the diode junction}~ (\mathrm{K})=\left({ }^{\circ} \mathrm{C}+273^{\circ}\right) \end{aligned}\]

and current The diode current equation relating the voltage

\[\boxed{I=I_o\left[\mathrm{e}^{\left(V / \eta V_T\right)}-1\right]}\]

When the diode is reverse biased, its current equation may be obtained by changing the sign of the applied voltage \(V\) .
\[I=I_o\left[\mathrm{e}^{\left(-V / \eta V_T\right)}-1\right]\]

Thus, the diode current with reverse bias is
If \(V \gg V_T\) , then the term \(\mathrm{e}^{\left(-V / \eta v_T\right)} \ll 1\) , therefore \(I \approx-I_o\) , termed as reverse saturation current , which is valid as long as the external voltage is below the breakdown value.

Load Lines

\[I_D=\frac{V_S-V_D}{R_s}\]

Load line

If \(V_s = 2~\mathrm{V}\) , \(R = 100~\Omega\)
\(V_D = 0 \Rightarrow I_D = 20~\mathrm{mA}\)
\(I_D = 0 \Rightarrow V_D = V_s = 2~\mathrm{V}\)
The straight line is called the load line
\(Q\) is an abbreviation for quiescent , which means “at rest.”

Problem-1

A germanium PN junction diode is forward biased with a voltage of 0.7 V applied across it. The diode has a saturation current of 10 \(\mu\) A and a forward bias resistance of 50 \(\Omega\) . Calculate the current flowing through the diode if the thermal voltage is 26 mV.

\[\begin{aligned} \text{Forward bias voltage}~V& = 0.7 ~ \text{V} \\ \text{Saturation current}~ I_s & = 10 \, \mu\text{A} = 10^{-5} \, \text{A} \\ \text{Forward bias resistance}~ R_f & = 50 \, \Omega \\ \text{Ideality factor}~ \eta &= 1 \\ \text{Thermal voltage}~ V_t & = 26 \, \text{mV} = 26 \times 10^{-3} \, \text{V} \\ \text{Diode equation:} ~ & I = I_s \left( e^{\frac{V}{\eta V_t}} - 1 \right) \\ & = 10^{-5} \left( e^{\frac{0.7}{1 \times 26 \times 10^{-3}}} - 1 \right) \\ & \approx 0.205 \, \text{A} \end{aligned}\]

Diode as a Rectifiers

Electrical power generated T & D as a.c. for economical reasons.
The alternating voltage is available at the mains but most of the electronic circuit need d.c. voltage for their operation.
Therefore the rectifier is needed to convert ac to dc.
The rectifier can be of two types:
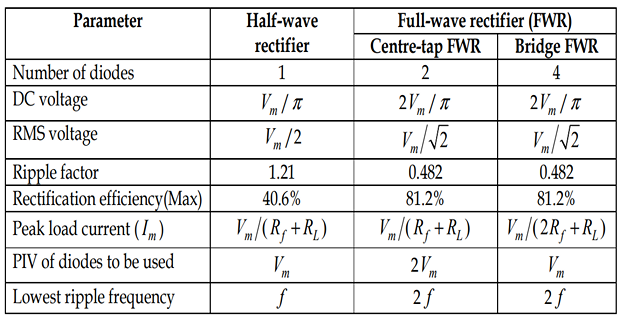
1. Half-Wave Rectifier
2. Full-Wave Rectifier

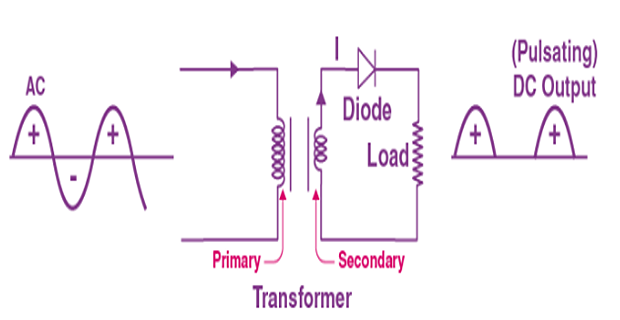
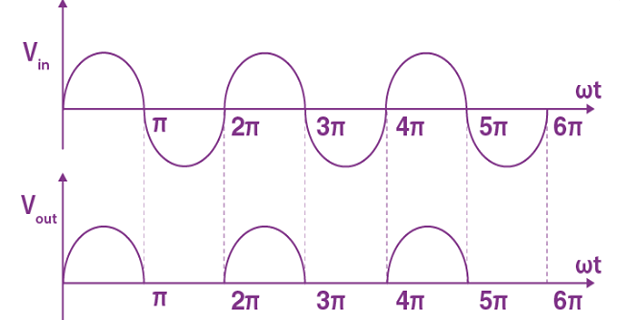
Half-Wave Rectifiers

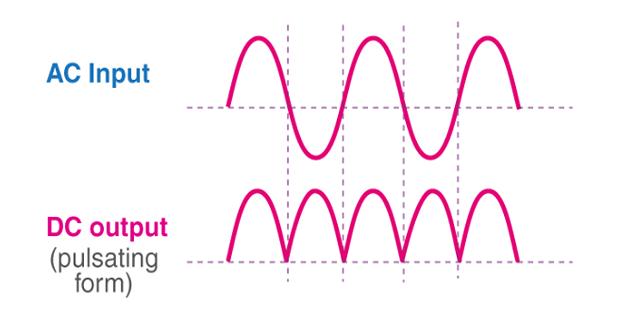
A half-wave rectifier is a simple electronic circuit that converts an alternating current (AC) input signal into a pulsating direct current (DC) output signal. It uses a diode as its main component.

Operation:

The AC input signal is applied to the primary side of a step-down transformer to reduce the voltage to a suitable level.
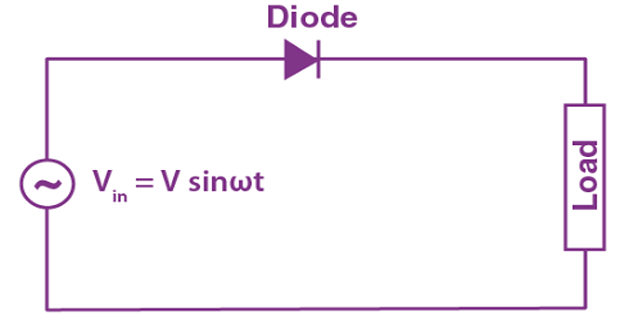
The transformed AC voltage is then applied to the diode, which acts as a one-way valve for electric current.
During the positive half-cycle of the AC input, the diode conducts and allows the current to flow through it, resulting in a positive voltage across the load resistor.
During negative half-cycle of AC input, diode becomes reverse-biased and blocks the current flow. Hence, no voltage is present across the load resistor during this period.
The output waveform of the rectifier is a pulsating DC voltage that only contains the positive half-cycles of the input signal.

Forward-Biased

Reverse-Biased

Full-cycle

Important formulas

Peak voltage (Vp): \(V_p = \dfrac{V_m}{\sqrt{2}}\)
Average voltage (Vavg): \(V_{\text{avg}} = \dfrac{V_p}{\pi}\)
Peak-to-Peak voltage (Vpp): \(V_{\text{pp}} = 2 \cdot V_p\)
RMS voltage (Vrms): \(V_{\text{rms}} = \dfrac{V_p}{\sqrt{2}}\)
Rectification Efficiency ( \(\eta\) ): \(\eta = \dfrac{V_{\text{avg}}}{V_{\text{rms}}} \times 100\%\)

Full-wave rectifiers

Significant power is lost while using a half-wave rectifier.
Full wave rectifiers provide a smooth and steady supply of power.
A full wave rectifier converts the complete cycle of alternating current into pulsating DC.
Full wave rectifiers utilize the full cycle of the input AC.
There are two methods to construct a full wave rectifier:
- Centre tapped rectifiers: Uses a centre tapped transformer and two diodes.
- Bridge rectifier: Uses a standard transformer with four diodes arranged as a bridge.

Centre-tapped Full-Wave Rectifiers

Consists of a centre tapped step-down TF and two diodes.
The output voltage is obtained across the connected load resistor.

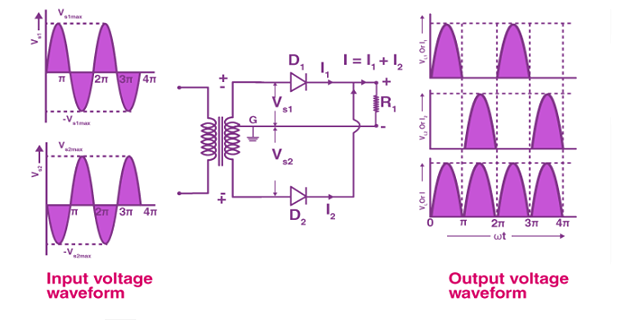
The step-down TF converts the HV AC into LV AC.
During the positive half cycle, diode D1 conducts as a short circuit while D2 acts as an open circuit.
During the negative half cycle, diode D1 acts as an open circuit while D2 conducts as a short circuit.
DC voltage is obtained for both positive and negative half cycles.

Bridge Rectifiers

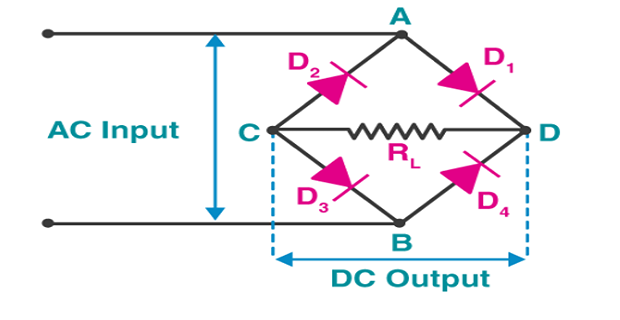
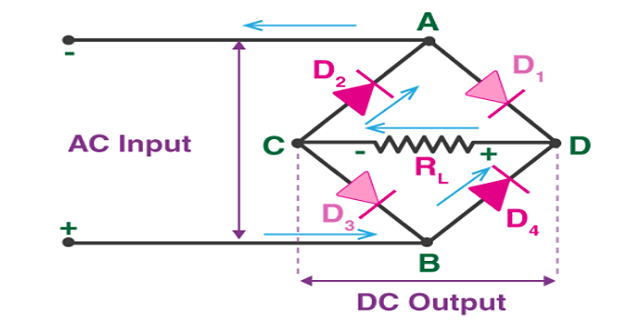
Important Formulas

Peak Inverse Voltage :
- maximum voltage a diode can withstand in the reverse-biased direction before breakdown.
- The PIV of the full-wave rectifier is double that of a half-wave rectifier.
- The PIV across D1 and D2 is \(2V_{\text{max}}\)
DC Output Voltage : \(V_{dc} = I_{avg}R_{L} = \dfrac{2}{\pi}I_{max}R_L\)
RMS Current : \(I_{rms} =\dfrac{I_{max}}{\sqrt{2}}\)
Rectification efficiency : \(\eta = \dfrac{\text{DC output power}}{\text{AC output power}}\)

Ripples in Rectified DC Output

Ripple refers to small fluctuations in the output voltage or current of a rectifier circuit.
It is caused by the pulsating nature of the rectified waveform.
The rectified waveform consists of positive and negative half cycles.
During the transition between half cycles, there is a brief period where the voltage or current decreases or crosses zero.
This transition period leads to fluctuations in the output, resulting in a ripple component superimposed on the DC signal.
Ripple is typically expressed as the peak-to-peak value or the root mean square (RMS) value of the fluctuation.
It is undesirable in applications requiring a steady and smooth DC voltage or current.
Ripple can cause distortions or malfunctions in sensitive electronic components.
Additional filtering or regulation techniques can be used to reduce the ripple and obtain a more stable DC output.

Summary

Problem-1

An a.c. supply of 230 V is applied to a half-wave rectifier circuit through a transformer of turn ratio 10:1. Find (i) the output d.c. voltage and (ii) the peak inverse voltage. Assume the diode to be ideal.

\[\begin{aligned} \text{Max. primary voltage}~V_{pm} &= \sqrt{2} \times 230 = 325.3~\mathrm{V} \\ \text{Max. secondary voltage}~V_{sm} & = V_{pm} \times \dfrac{N_2}{N_1} = 325.3\times\dfrac{1}{10} = 32.53~\mathrm{V}\\ V_{dc} & = I_{dc} \times R_L\\ & = \dfrac{I_m}{\pi} \times R_L = \dfrac{V_{sm}}{\pi} = \dfrac{32.53}{\pi} = 10.36~\mathrm{V}\\ \text{PIV} & = V_{sm} = 32.53~\mathrm{V} \\ \end{aligned}\]

Problem-2

A crystal diode having internal resistance \(R_f = 20~\Omega\) is used for half-wave rectification. If the applied voltage \(v = 50 \sin \omega t\) and load resistance \(R_L= 800~\Omega\) , find : (i) \(I_m\) , \(I_{dc}\) , \(I_{rms}\) (ii) a.c. power input and d.c. power output (iii) d.c. output voltage (iv) efficiency of rectification.

\[\begin{aligned} v&=50 \sin \omega t \Rightarrow V_m =50 \mathrm{~V}\\ I_m&=\frac{V_m}{r_f+R_L}=\frac{50}{20+800}=0.061 \mathrm{~A}=61 \mathrm{~mA} \\ I_{d c} & =I_m / \pi=61 / \pi=19.4 \mathrm{~mA} \\ I_{r m s} & =I_m / 2=61 / 2=30.5 \mathrm{~mA} \end{aligned}\]

\[\begin{aligned} \text{a.c. power input}&=\left(I_{r m s}\right)^2 \times\left(R_f+R_L\right)\\ &=\left(\frac{30.5}{1000}\right)^2 \times(20+800)=0.763~\mathrm{W}\\ \text{d.c. power output}&=I_{d c}^2 \times R_L=\left(\frac{19.4}{1000}\right)^2 \times 800=0.301~\mathrm{W} \\ \text{d.c. output voltage}&=I_{d c} R_L=19.4 \mathrm{~mA} \times 800 \Omega=15.52~\mathrm{V} \\ \text{Efficiency of rectification}&=\frac{0.301}{0.763} \times 100=39.5 \% \end{aligned}\]

Problem-3

A half-wave rectifier is used to supply \(50 ~\mathrm{~V}\) d.c. to a resistive load of \(800~ \Omega\) . The diode has a resistance of \(25~ \Omega\) . Calculate a.c. voltage required.

\[\begin{aligned} \text { Output d.c. voltage, } V_{d c} & =50 \mathrm{~V} \\ \text { Diode resistance, } r_f & =25 \Omega \\ \text { Load resistance, } R_L & =800 \Omega \end{aligned}\]

be the maximum value of a.c. voltage required. Let

Problem-4

A full-wave rectifier uses two diodes, the internal resistance of each diode may be assumed constant at \(20~ \Omega\) . The transformer r.m.s. secondary voltage from centre tap to each end of secondary is \(50~ \mathrm{~V}\) and load resistance is \(980~ \Omega\) . Find : (i) the mean load current (ii) the r.m.s. value of load current.

\[\begin{aligned} r_f & =20 \Omega, \quad R_L=980 \Omega \\ \text { Max. a.c. voltage, } V_m & =50 \times \sqrt{2}=70.7 \mathrm{~V} \\ \text { Max. load current, } I_m & =\frac{V_m}{r_f+R_L}=\frac{70.7 \mathrm{~V}}{(20+980) \Omega}=70.7 \mathrm{~mA}\\ I_{d c}&=\frac{2 I_m}{\pi}=\frac{2 \times 70.7}{\pi}=45 \mathrm{~mA}\\ I_{r m s}&=\frac{I_m}{\sqrt{2}}=\frac{70.7}{\sqrt{2}} =50 \mathrm{~mA} \end{aligned}\]

Problem-5

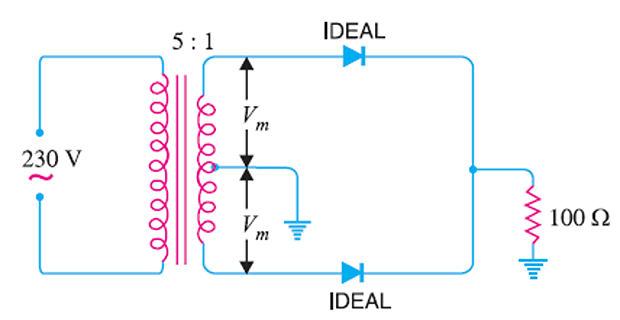
In the centre-tap circuit, the diodes are assumed to be ideal i.e. having zero internal resistance. Find :(i) d.c. output voltage(ii) peak inverse voltage (iii) rectification efficiency.

\[\begin{aligned} V_p & = 230~\mathrm{V} \\ V_s & = 230 \times (1/5) = 46~\mathrm{V} \\ V_{sm} & = 46 \times \sqrt{2} = 65~\mathrm{V} \end{aligned}\]

\[\begin{aligned} I_{rms} & = \dfrac{I_m}{\sqrt{2}} = \dfrac{V_m}{\sqrt{2}\times R_L} = \dfrac{32.5}{\sqrt{2}\times 100} = 0.229~\mathrm{A} \\ \text{Rect. efficiency}~\eta & = \dfrac{I_{dc}^2\times R_L}{I_{rms}^2\times R_L} = 81.7\% \end{aligned}\]