Sum of Products (SOP) & Product of Sums (POS)
Sum of Products (SOP)
-
SOP is a standard form of Boolean expression where the output is a sum (OR) of product (AND) terms
-
Each product term is a minterm, representing a specific combination of inputs where the function equals 1
-
Example: For variables \(A, B\), SOP expression: \(F = A'B + AB'\)
-
Minterms for a 3-variable function (\(A, B, C\)):
-
\(m_0 = A'B'C'\), \(m_1 = A'B'C\), \(m_2 = A'BC'\), \(m_3 = A'BC\)
-
\(m_4 = AB'C'\), \(m_5 = AB'C\), \(m_6 = ABC'\), \(m_7 = ABC\)
-
-
General form: \(F = \sum m_i\) where \(m_i\) are the required minterms
Product of Sums (POS)
-
POS is a standard form where the output is a product (AND) of sum (OR) terms
-
Each sum term is a maxterm, representing combinations where the function equals 0
-
Example: For variables \(A, B\), POS expression: \(F = (A + B)(A' + B')\)
-
Maxterms for a 3-variable function (\(A, B, C\)):
-
\(M_0 = A + B + C\), \(M_1 = A + B + C'\), \(M_2 = A + B' + C\), \(M_3 = A + B' + C'\)
-
\(M_4 = A' + B + C\), \(M_5 = A' + B + C'\), \(M_6 = A' + B' + C\), \(M_7 = A' + B' + C'\)
-
-
General form: \(F = \prod M_i\) where \(M_i\) are the required maxterms
SOP vs POS: Example
-
Consider a 2-variable function with truth table:
| A | B | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
-
SOP form: \(F = A'B' + AB' = B'(A' + A) = B'\)
-
POS form: \(F = (A' + B')(A + B') = B'\)
-
Both forms simplify to the same expression: \(F = B'\)
Karnaugh Maps (K-Maps)
Karnaugh Maps: Introduction
-
A graphical method to simplify Boolean expressions systematically
-
Reduces the number of terms and operations in a Boolean function
-
Organizes minterms in a grid to identify patterns for simplification
-
Adjacent cells differ by only one variable (Gray code ordering)
-
Commonly used for 2, 3, and 4 variables
Key Rules:
-
Group adjacent 1s in powers of 2 (1, 2, 4, 8, ...)
-
Larger groups lead to greater simplification
-
Groups can wrap around edges
2-Variable K-Map
-
For variables \(A, B\), a 2×2 grid is used
-
Each cell represents a minterm

Example: If \(F = A'B' + A'B\), we get:
-
Group cells \(m_0\) and \(m_1\) (top row)
-
Simplified form: \(F = A'\)
3-Variable K-Map
-
For variables \(A, B, C\), a 2×4 grid is used
-
Columns follow Gray code: \(B'C', B'C, BC, BC'\)
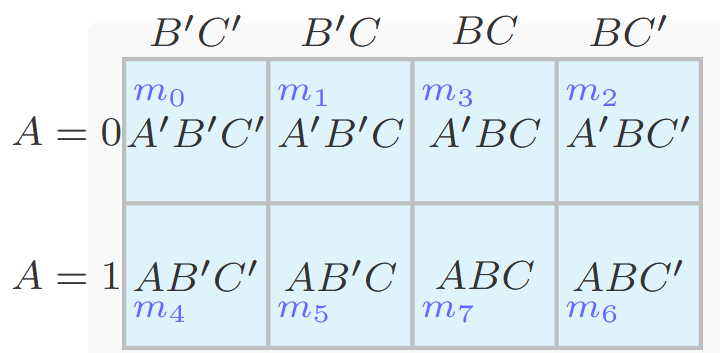
Note: Adjacent cells horizontally and vertically differ by one variable
4-Variable K-Map
-
For variables \(A, B, C, D\), a 4×4 grid is used
-
Both rows and columns follow Gray code ordering
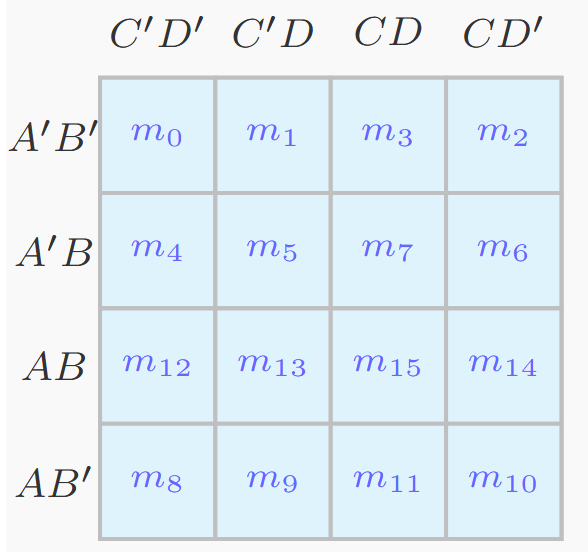
Remember: Corner cells are also adjacent (wrap-around effect)
K-Map Simplification Example
Example: Simplify \(F(A,B,C) = \sum m(1,3,5,7)\)

-
Group the four 1s in the middle columns
-
The group eliminates variables \(A\) and \(B'\) vs \(B\)
-
Simplified expression: \(F = C\)
Combinational Logic Components
Multiplexers (MUX)
-
A multiplexer selects one of many input signals and forwards it to a single output
-
Structure: \(2^n\) input lines, \(n\) select lines, 1 output
-
Also called "data selector"
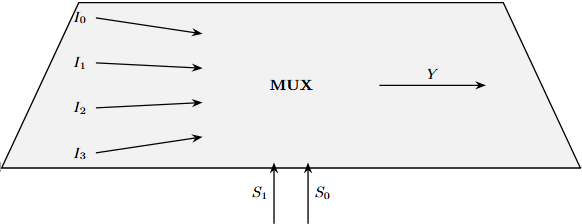
4:1 MUX Truth Table
| \(S_1\) | \(S_0\) | Output |
|---|---|---|
| 0 | 0 | \(I_0\) |
| 0 | 1 | \(I_1\) |
| 1 | 0 | \(I_2\) |
| 1 | 1 | \(I_3\) |
Demultiplexers (DEMUX)
-
A demultiplexer takes a single input and routes it to one of \(2^n\) outputs
-
Structure: 1 input, \(n\) select lines, \(2^n\) outputs
-
Also called "data distributor"
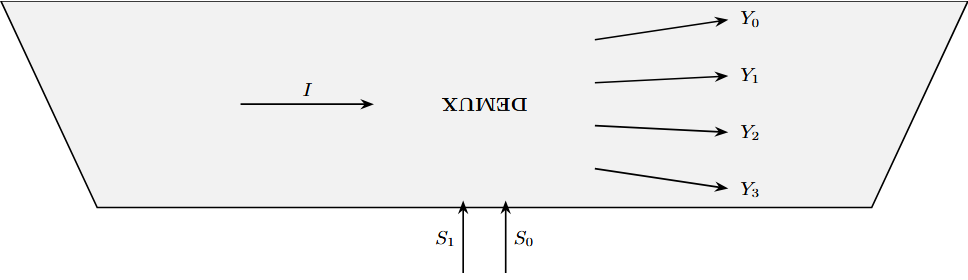
Applications: Data routing, memory addressing, LED displays
Encoders
-
Converts multiple input lines into fewer output lines (binary code)
-
\(2^n\) inputs \(\to\) \(n\) outputs
-
Only one input should be active at a time
Truth Table:
| \(I_3\) | \(I_2\) | \(I_1\) | \(I_0\) | \(Y_1\) | \(Y_0\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Priority Encoder
-
Handles multiple simultaneous inputs by assigning priorities
-
Higher-numbered inputs have higher priority
-
Includes a valid output to indicate if any input is active
4:2 Priority Encoder Truth Table:
| \(I_3\) | \(I_2\) | \(I_1\) | \(I_0\) | \(Y_1\) | \(Y_0\) | \(V\) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | X | X | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
Applications: Interrupt handling, data compression
Decoders
-
Converts binary input into multiple output lines
-
\(n\) inputs \(\to\) \(2^n\) outputs
-
Only one output is active (HIGH) for each input combination
Truth Table:
| \(A_1\) | \(A_0\) | \(Y_3\) | \(Y_2\) | \(Y_1\) | \(Y_0\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
Applications & Summary
Applications of Combinational Circuits
Multiplexers
-
Data routing in communication systems
-
Function generators using MUX
-
CPU data path selection
Decoders:
-
Memory address decoding
-
7-segment display drivers
-
Instruction decoding in processors
Encoders:
-
Keyboard input encoding
-
Priority interrupt systems
-
Data compression
Summary
Key Concepts Covered:
-
SOP & POS: Standard forms for Boolean expressions
-
K-Maps: Graphical method for Boolean simplification
-
MUX/DEMUX: Data selection and distribution
-
Encoders/Decoders: Code conversion circuits
Important Points:
-
K-Maps provide systematic simplification for up to 4 variables
-
Combinational circuits have no memory - output depends only on current inputs
-
These building blocks form the foundation of digital systems
Next: Sequential Logic Circuits (Flip-flops, Counters, Registers)