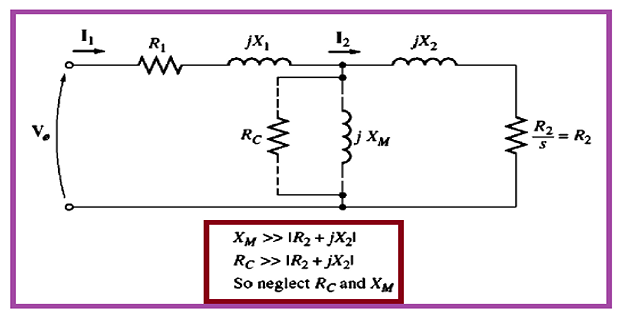
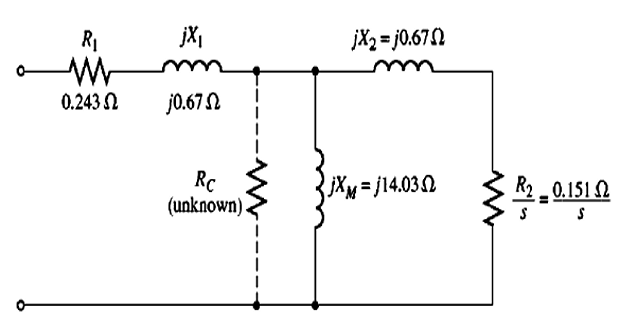
Solution-1
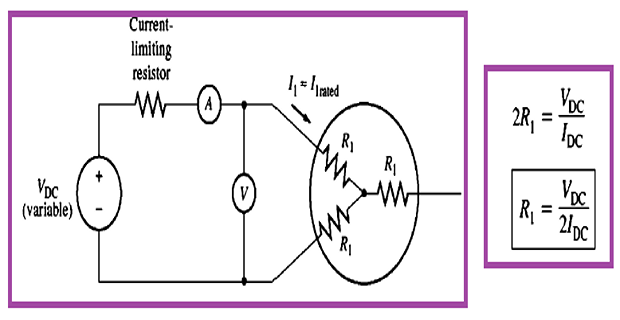
DC Test:
The following test data were taken on a 7.5 HP, 4-pole, 208-V, 60-Hz, Y-connected induction motor having a rated current of 28 A.
DC test: \[\mathrm{V_{DC}} = 13.6~\mathrm{V} \quad \quad \mathrm{I_{DC}} = 28.0~\mathrm{A}\]
| No-load test: | Locked rotor test: | ||||||
| \(V_{T}\) | = | 208 V | \(V_{T}\) | = | 25 V | ||
| \(I_{A}\) | = | 8.12 A | \(I_{A}\) | = | 28.1 A | ||
| \(I_{B}\) | = | 8.20 A | \(I_{B}\) | = | 28.0 A | ||
| \(I_{C}\) | = | 8.18 A | \(I_{C}\) | = | 27.6 A | ||
| \(f\) | = | 60 Hz | \(f\) | = | 15 Hz | ||
| \(P_{in}\) | = | 420 W | \(P_{in}\) | = | 920 W | ||
Sketch the per-phase equivalent circuit
Find the slip at the pull-out torque
Find the value of the pull-out torque
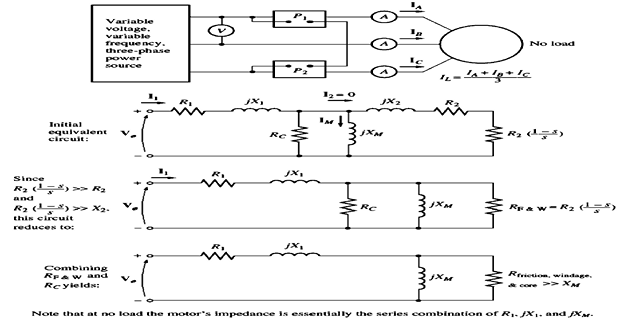
Equivalent Circuit:
From DC Test: \[\mathrm{R_{DC}} = \dfrac{V_{DC}}{2I_{DC}}=\dfrac{13.6}{2\times 28}=0.243~\Omega\]
From No-load Test: \[\begin{aligned} I_{\mathrm{L}, \mathrm{av}} &=\frac{8.12 \mathrm{~A}+8.20 \mathrm{~A}+8.18 \mathrm{~A}}{3}=8.17 \mathrm{~A} \\ V_{\phi, \mathrm{nl}} &=\frac{208 \mathrm{~V}}{\sqrt{3}}=120 \mathrm{~V} \\ \left|Z_{\mathrm{nl}}\right| &=\frac{120 \mathrm{~V}}{8.17 \mathrm{~A}}=14.7 \Omega=X_{1}+X_{M} \\ P_{\mathrm{SCL}} &=3 I_{1}^{2} R_{1}=3(8.17 \mathrm{~A})^{2}(0.243 \Omega)=48.7 \mathrm{~W} \\ P_{\text {rot,nl }} &=P_{\text {in.nl }}-P_{\text {SCL.nl }} \\ &=420 \mathrm{~W}-48.7 \mathrm{~W}=371.3 \mathrm{~W} \end{aligned}\]
From Locked-Rotor Test: \[\begin{aligned} I_{\mathrm{Lav}}&=\frac{28.1 \mathrm{~A}+28.0 \mathrm{~A}+27.6 \mathrm{~A}}{3}=27.9 \mathrm{~A} \\ \left|Z_{\mathrm{LR}}\right|&=\frac{V_{\phi}}{I_{A}}=\frac{V_{T}}{\sqrt{3} I_{A}}=\frac{25 \mathrm{~V}}{\sqrt{3}(27.9 \mathrm{~A})}=0.517 \Omega \\ \theta&=\cos ^{-1} \frac{P_{\mathrm{in}}}{\sqrt{3} V_{T} I_{L}} =\cos ^{-1} \frac{920 \mathrm{~W}}{\sqrt{3}(25 \mathrm{~V})(27.9 \mathrm{~A})} \\ &=\cos ^{-1} 0.762=40.4^{\circ} \\ R_{\mathrm{LR}}&=0.517 \cos 40.4^{\circ}=0.394 \Omega=R_{1}+R_{2} \\ R_{1}&=0.243 \Omega~~(\text{Given}) \Rightarrow R_{2}=0.151 \Omega \\ X_{\mathrm{LR}}^{\prime}&=0.517 \sin 40.4^{\circ}=0.335 \Omega ~~(\text{at 15 Hz})\\ X_{\mathrm{LR}}&=\frac{f_{\text {rated }}}{f_{\text {test }}} X_{\mathrm{LR}}^{\prime}=\left(\frac{60 \mathrm{~Hz}}{15 \mathrm{~Hz}}\right) 0.335 \Omega=1.34 \Omega \\ X_{1}&=X_{2}=0.67 \Omega \\ X_{M}&=\left|Z_{\text {nl }}\right|-X_{1}=14.7 \Omega-0.67 \Omega=14.03 \Omega \end{aligned}\]
For this equivalent circuit, the Thevenin equivalents \[V_{\mathrm{TH}}= 114.6 \mathrm{~V} \quad R_{\mathrm{TH}}=0.221 \Omega \quad X_{\mathrm{TH}}=0.67 \Omega\]
The slip at the pull-out torque: \[\begin{aligned} s_{\max } &=\frac{R_{2}}{\sqrt{R_{\mathrm{TH}}^{2}+\left(X_{\mathrm{TH}}+X_{2}\right)^{2}}} \\ &=\frac{0.151 \Omega}{\sqrt{(0.243 \Omega)^{2}+(0.67 \Omega+0.67 \Omega)^{2}}}=0.111=11.1 \% \end{aligned}\]
The maximum torque of this motor \[\begin{aligned} \tau_{\max } &=\frac{3 V_{\mathrm{TH}}^{2}}{2 \omega_{\text {sync }}\left[R_{\mathrm{TH}}+\sqrt{\left.R_{\mathrm{TH}}^{2}+\left(X_{\mathrm{TH}}+X^{2}\right)\right]}\right.} \\ &=\frac{3(114.6 \mathrm{~V})^{2}}{2(188.5 \mathrm{rad} / \mathrm{s})\left[0.221 +\sqrt{(0.221 )^{2}+(0.67 +0.67 )^{2}}\right]} \\ &=66.2 \mathrm{~N} \cdot \mathrm{m} \end{aligned}\]