Demonstrative Video
\(\bullet\) Transformer with resistance and
leakage reactance
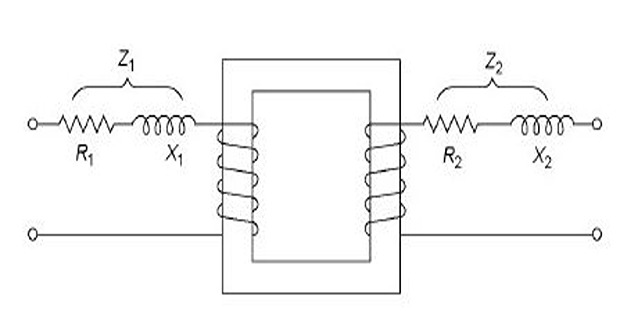
\[\begin{aligned}
Z_{1} & =\sqrt{\left(R_{1}^{2}+X_{1}^{2}\right)}\\
Z_{2} & =\sqrt{\left(R_{2}^{2}+X_{2}^{2}\right)}\\
V_{1} & =E_{1}+I_{1}\left(R_{1}+jX_{1}\right)=E_{1}+I_{1}Z_{1}\\
E_{2} & =V_{2}+I_{2}\left(R_{2}+jX_{2}\right)=V_{2}+I_{2}Z_{2}
\end{aligned}\]
\[\begin{array}{ccc}
X_{2}^{'}=X_{2}/K^{2} & \mbox{and} &
X_{1}^{'}=K^{2}X_{1}\\
X_{01}=X_{1}+X_{2}^{'} & \mbox{and} &
X_{02}=X_{2}+X_{1}^{'}
\end{array}\]
Leakage reactance can also be transferred from one winding to the
other in the same way as resistance
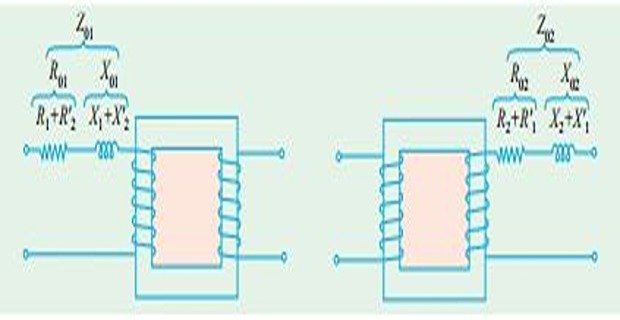
\[\begin{aligned}
Z_{01} & =\sqrt{\left(R_{01}^{2}+X_{01}^{2}\right)}\\
Z_{02} & =\sqrt{\left(R_{02}^{2}+X_{02}^{2}\right)}
\end{aligned}\]
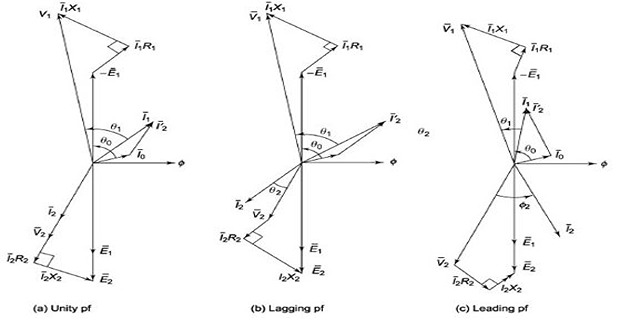
Voltage Drop in a Transformer
\[\begin{aligned}
V_{1} & \thickapprox E_{1}\\
E_{2} & =KE_{1}=KV_{1}\\
E_{2} & =_{0}V_{2}
\end{aligned}\]
At no load:
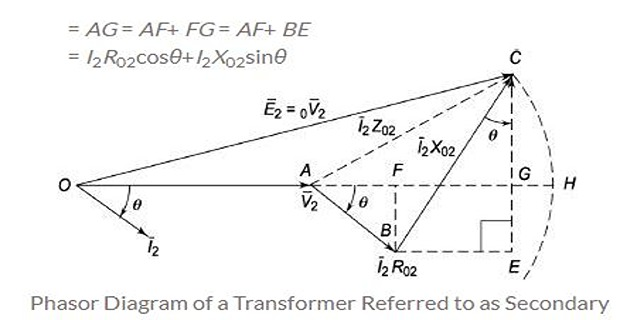
\[I_{2}R_{02}\cos\Phi\pm
I_{2}X_{02}\sin\Phi\]
\(-\)\(+\)The approximate voltage drop is:
\[I_{1}R_{01}\cos\Phi\pm
I_{1}X_{01}\sin\Phi\]
\[\begin{aligned}
v_{r} &
=\dfrac{I_{2}R_{02}}{_{0}V_{2}}\times100=\dfrac{I_{1}R_{01}}{V_{1}}\times100=\mbox{percentage
resistive drop}\\
v_{x} &
=\dfrac{I_{2}X_{02}}{_{0}V_{2}}\times100=\dfrac{I_{1}X_{01}}{V_{1}}\times100=\mbox{percentage
reactive drop}
\end{aligned}\]
\[\begin{aligned}
= & \dfrac{I_{2}R_{02}cos\Phi\pm
I_{2}X_{02}sin\Phi}{_{0}V_{2}}\times100\\
= & v_{r}cos\Phi\pm v_{x}sin\Phi
\end{aligned}\]
Similarly, approximate voltage drop referred to primary is
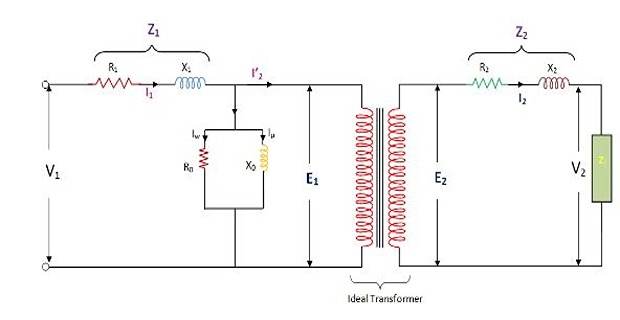
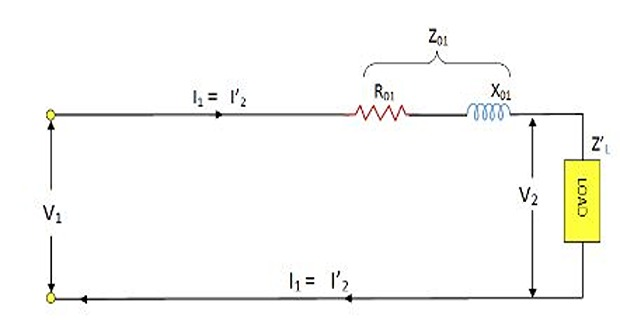
Equivalent Circuit of a Transformer
Equivalent circuit is basically a diagram in which the resistance and
leakage reactance of the transformer are imagined to be external to the
winding
The equivalent circuit diagram of transformer is given below:-
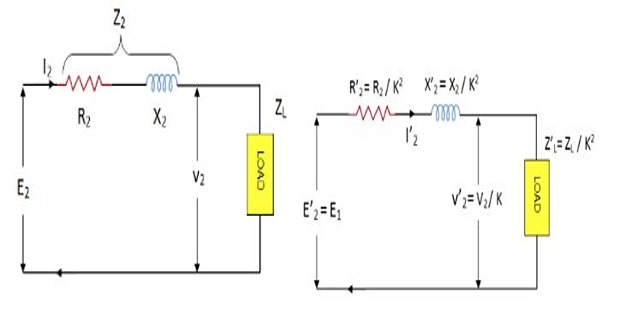
The secondary circuit and its equivalent primary value
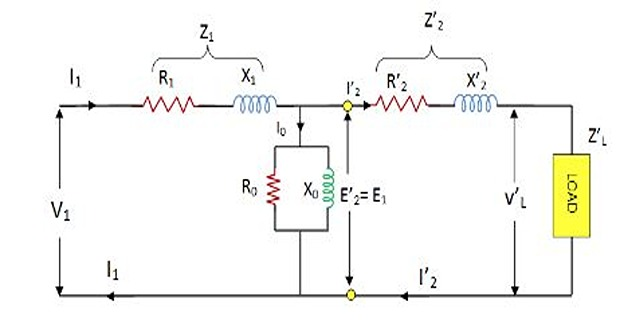
The total equivalent circuit is obtained by adding in the primary
impedance
It can be simplified
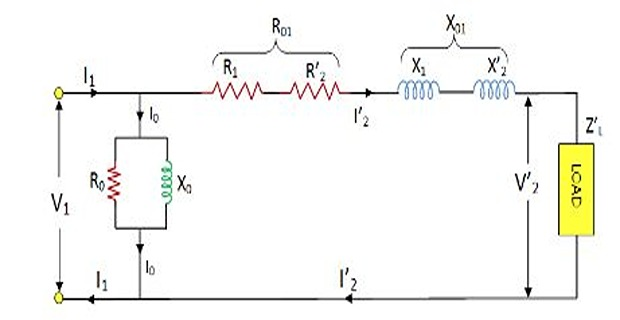
At last, the circuit is simplified by omitting \(I_0\) altogether
\[\begin{aligned}
Z &
=Z_{1}+Z_{m}||\left(Z_{2}^{'}+Z_{L}^{'}\right)\\
&
=Z_{1}+\dfrac{Z_{m}\left(Z_{2}^{'}+Z_{L}^{'}\right)}{Z_{m}+\left(Z_{2}^{'}+Z_{L}^{'}\right)}
\end{aligned}\]
\[V_{1}=I_{1}\left[Z_{1}+\dfrac{Z_{m}\left(Z_{2}^{'}+Z_{L}^{'}\right)}{Z_{m}+\left(Z_{2}^{'}+Z_{L}^{'}\right)}\right]\]
The total impedance between the input terminal:








