Demonstrative Video
Case-1: Transformer on no-load
Even under no-load \(I_1\) is not wholly reactive
Under no-load, \(I_1 = I_0\) has to supply
Iron loss in the core: Hysteresis and eddy current loss
very small amount of copper loss in the primary winding alone (\(I_2=0\))
Hence, \(I_0\) is not at \(90^{\circ}\) behind \(V_1\), but lags by \(\Phi_0 < 90^{\circ}\)
No-load input power:
\[W_0=V_1I_0\cos(\Phi_0)\]
where \(\cos(\Phi_0)\) is primary power factor under no-load condition
\[ \begin{aligned} I_w &=I_0\cos(\Phi_0)\\ I_m &=I_0\sin(\Phi_0) \end{aligned} \] \[I_0=\sqrt{I_w^2+I_m^2}\]
\[I_0=\sqrt{I_w^2+I_m^2}\]Important points:
\(I_0\) is very small about 1% of the full-load primary current
As \(I_0\) is very small, no-load primary Cu loss is negligibly small, means no-load primary input is practically equal to the iron loss in the transformer
As core loss is responsible for the shift in the current vector, \(\Phi_0\) is known as the hysteresis angle of advance
Since, Core \(\mu\) varies with the instantaneous value of \(I_m\), hence wave of \(I_m\) is not truly sinusoidal. Thus it should not be represented by vector (only sinusoids are represented by vectors), but it makes no difference
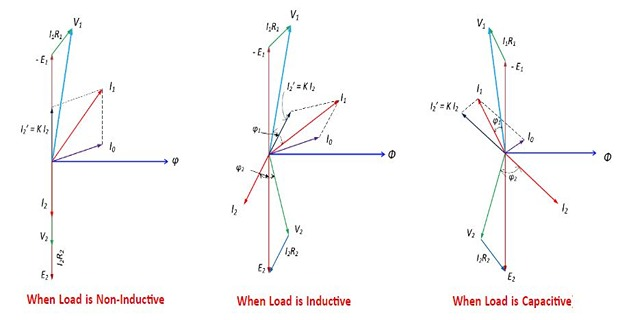
Case-2: Transformer on load
When the transformer is on loaded condition, the secondary of the transformer is connected to load.
The load can be resistive, inductive or capacitive.
The current \(I_2\) flows through the secondary winding of the transformer.
\(\left|I_2\right|\) depends on \(V_2\) and the load impedance.
The phase angle between \(I_2\) and \(V_2\) depends on the nature of the load.
Operation of the Transformer on Load Condition
When secondary of the transformer is kept open, it draws the no-load current from the main supply.
The no-load current induces the magnetomotive force \(N_1I_0\) and this force set up the flux \(\Phi\) in the core of the transformer.
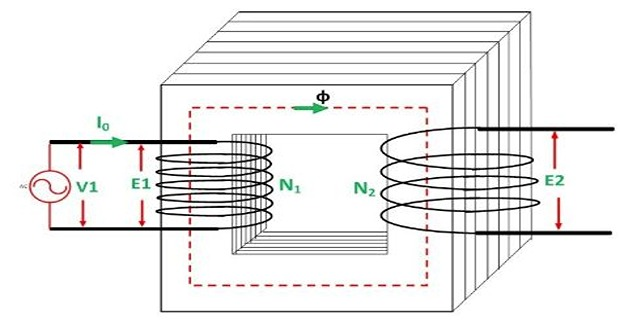
When the load is connected \(I_2\) flows through secondary winding.
\(I_2\) induces \(N_2I_2\) on the secondary winding of the transformer.
This force set up \(\Phi_2\) in the transformer core.
\(\Phi_2\) oppose the flux \(\Phi\), according to Lenz’s law

As \(\Phi_2\) opposes \(\Phi\), the resultant flux decreases and reduces the induces EMF \(E_1\).
Thus, strength of \(V_1\) is more than \(E_1\) and an additional primary current \(I_1^{'}\) drawn from the main supply.
The additional current is used for restoring the original value of the flux in the core so that \(V_1 = E_1\).
The primary current \(I_1^{'}\) is in phase opposition with \(I_2\). Thus, it is called the primary counter balancing current.
\(I_1^{'}\) induces \(N_1I_1^{'}\) that set up \(\Phi_1^{'}\).
The direction of the flux is same as that of the \(\Phi\) and it cancels \(\Phi_2\) which induces because of the \(N_2I_2\)
Now, \(N_1I_1^{'} = N_2I_2\)
\[I_1^{'}=\left(\frac{N_2}{N_1}\right)I_2=KI_2\]Therefore,
\[\overrightarrow{I_1}=\overrightarrow{I_0}+\overrightarrow{I_1^{'}}\]
Practical Transformer
\(\bullet\) Transformer with winding Resistance but No Magnetic Leakage
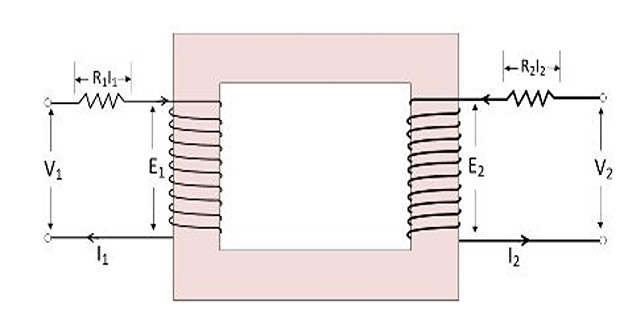
\(\bullet\) Equivalent Resistance

Resistance of two winding can be transferred to any one winding
The advantage of concentrating both the resistances in one winding is that it makes calculations very simple and easy because one has to work in one winding only
The equivalent secondary resistance as referred to primary:
\[R_2^{'}\to R_2/K^2\]- \[\begin{aligned} I_{2}^{2}R_{2} & =I_{1}^{2}R_{2}^{'}\\ \Rightarrow R_{2}^{'} & =\left(I_{2}/I_{1}\right)^{2}R_{2}\\ \Rightarrow R_{2}^{'} & =R_{2}/K^{2} \end{aligned}\]\(\left(I_2/I_1\right) = 1/K\)\(I_0\) in secondary Equivalent resistance in primary which would have caused the same loss as
Similarly, equivalent primary resistance as referred to secondary:
\[R_1^{'}=K^2R_1\]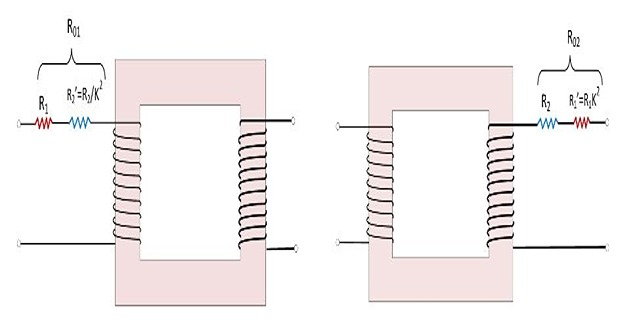
Effective resistance referred
\[\begin{aligned} R_{01} & =R_{1}+R_{2}^{'}=R_{1}+R_{2}/K^{2}\\ R_{02} & =R_{2}+R_{1}^{'}=R_{2}+K^{2}R_{1} \end{aligned}\]\(\bullet\) Magnetic Leakage flux in transformer
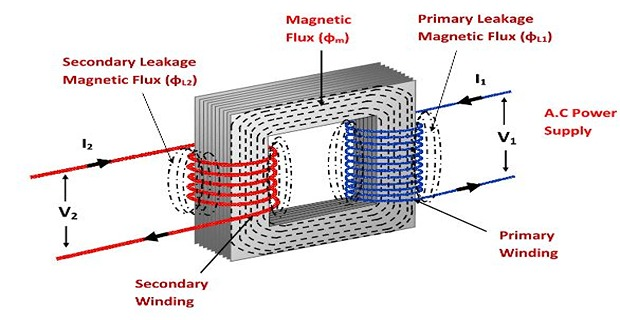
It is impossible to link all the flux with \(N_1\) and \(N_2\)
All the flux linked with \(N_1\) does not link \(N_2\) but part of it i.e. \(\Phi_{L_{1}}\) completes its magnetic circuit by passing through air rather than through the core
The primary leakage flux is produced due to primary ampere-turns (mmf)
\(\Phi_{L_{1}}\) is in phase with \(I_1\) and induces \(e_{L_{1}}\) in primary but not in secondary
Similarly the case for secondary leakage flux \(\Phi_{L_{2}}\)
At no or light load, primary and secondary ampere-turns are small, hence leakage fluxes are negligible
As load increased both winding carry huge currents generating large mmf, hence there is leakage flux