Master Torque: Unveiling Torque Development by Field Alignment

Following cases are considered to understand the process of torque development by the alignment of two fields:
- Soft iron piece placed in the magnetic field.
- Permanent magnet placed in the magnetic field.
- Electromagnet placed in the magnetic field.

Consider a soft iron piece, capable of free rotation, placed in the magnetic field of two permanent magnets
The magnetic lines of force are set up in the soft iron piece

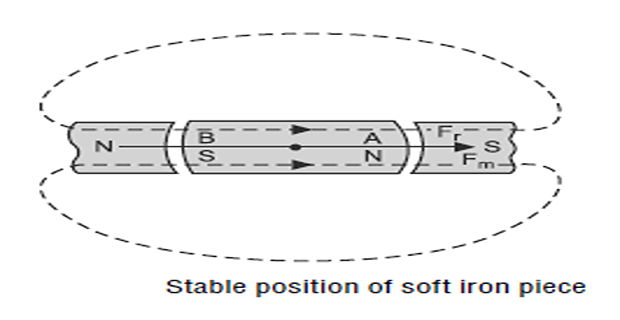
The molecular poles get aligned parallel to the magnetic field due to magnetic induction.
The soft iron piece obtains the polarities as marked
This is the stable position of the soft iron piece.
Torque produce in this case is zero.

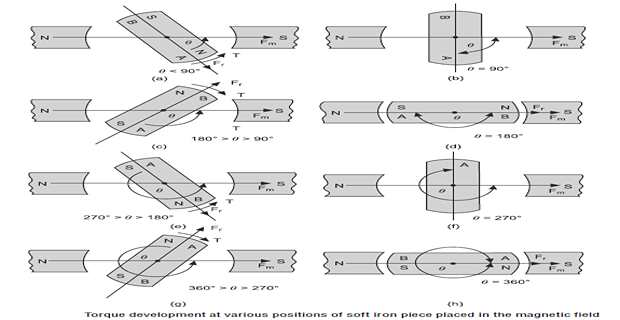
If the soft iron piece is rotated through an angle \(\theta (\theta < 90^{\circ})\), then by magnetic induction, ends A and B become North and South poles respectively.

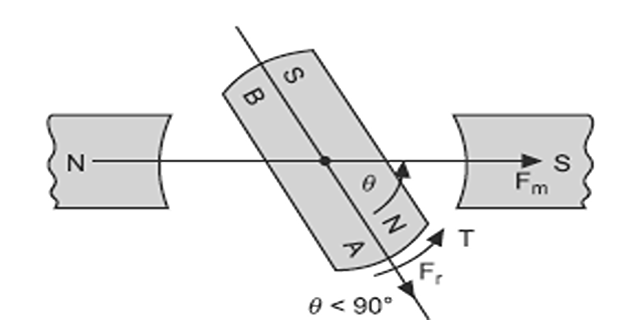
A force of attraction acts on the two ends and the soft iron piece will try to come in line with the main field i.e., the position of least reluctance path.
This anticlockwise torque tries to decrease the angle \(\theta\) and is considered as negative.

When soft iron piece is rotated through an angle \(\theta=90^{\circ}\), an equal force of attraction and repulsion acts on each end of short iron piece therefore, torque produced is zero.

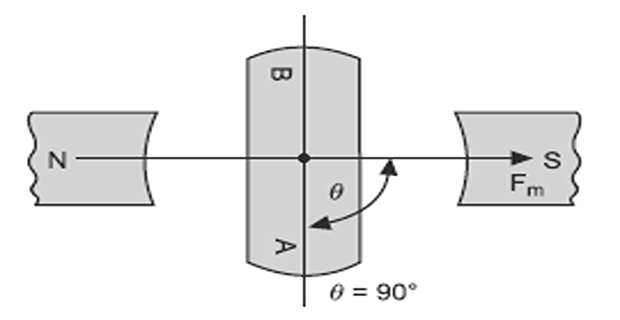
This is the unstable position of the soft iron piece, because a slight change in angle \(\theta\) in either direction will create a torque in that direction.

When soft iron piece is rotated through an angle \(\theta (\theta > 90^{\circ})\), then by magnetic induction ends, A and B become South and North poles respectively.

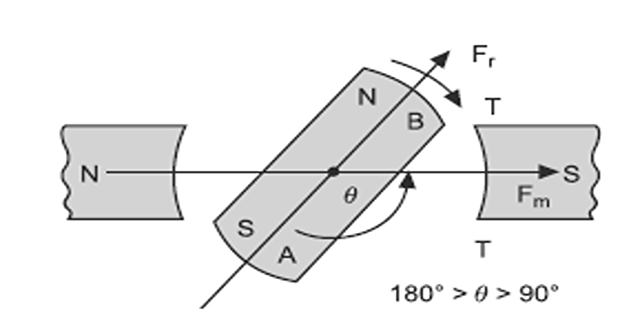
A force of attraction acts on the ends and soft iron piece will try to come in line with the main field.
This clockwise torque tries to increase the angle \(\theta\) and is considered as positive

When soft iron piece is rotated through an angle \(\theta = 180^{\circ}\), then by magnetic induction, ends A and B will obtain South and North polarity respectively

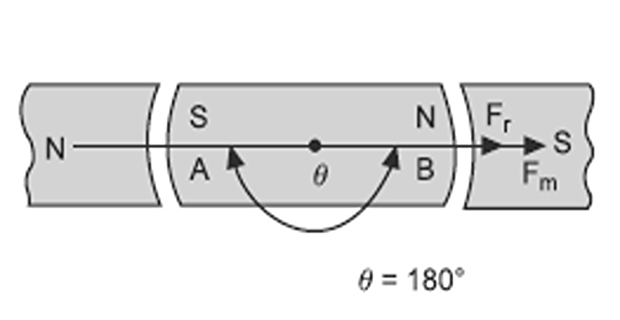
There is a force of attraction at ends A as well as at B of soft iron piece which being equal and opposite cancel each other.
In this position, torque produced is zero.
This is the stable position, because any change in angle \(\theta\) will create a torque which will tend to restore it position

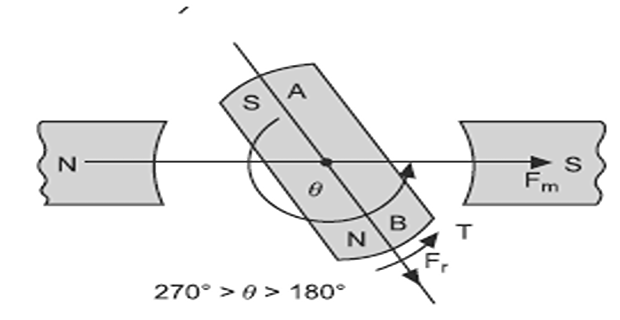
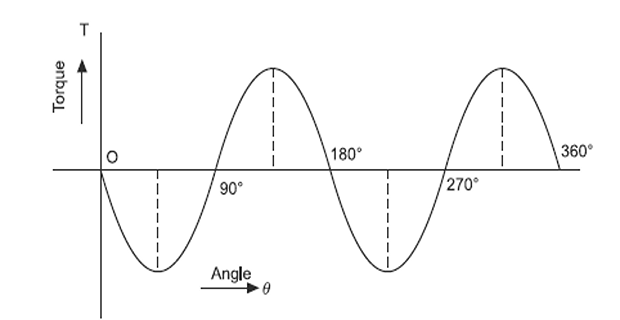
Between \(180^{\circ}\) to \(360^{\circ}\) torque is
- \(270^{\circ}>\theta>180^{\circ}\), negative (anticlockwise) .
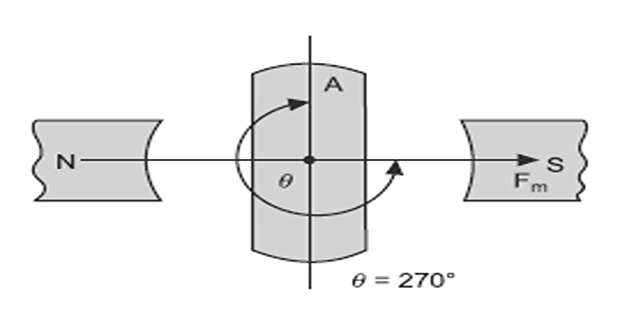
- \(\theta=270^{\circ}\), zero, and it is an unstable position .
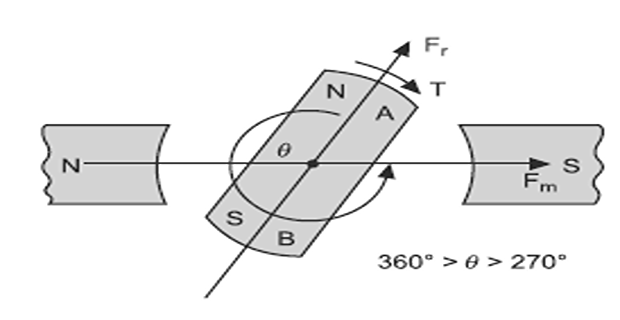
- \(360^{\circ}>\theta>270^{\circ}\), positive (clockwise)
- \(\theta=360^{\circ}\), zero and it is a stable position.

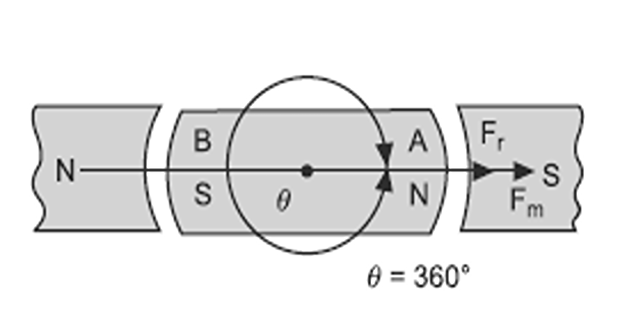
When a soft iron piece is placed in the magnetic field, by magnetic induction iron piece is magnetised.
The magnetised iron piece produces its own field, the axis of that field is shown by arrow head \(F_r\).
The axis of the main magnetic field is shown by the arrowhead \(F_m\).
The rotor field \(F_r\) tries to come in line with \(F_m\) due to which torque develops.
Hence, it can be said that torque is developed by the alignment of two fields.
The angle between two magnetic fields on which torque depends is called torque angle.
Torque angle is measured with respect to the direction to the direction of rotation of soft iron piece

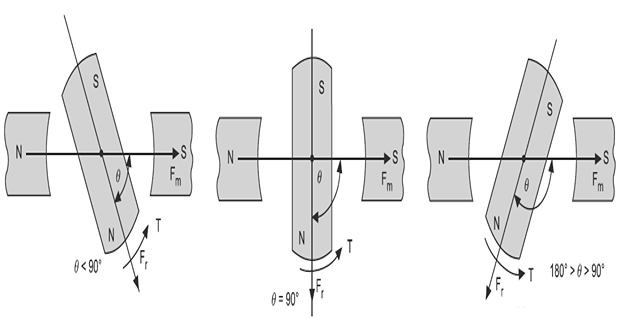
There is a force of attraction on north and south pole of the rotating magnet, which being equal and opposite cancel each other.

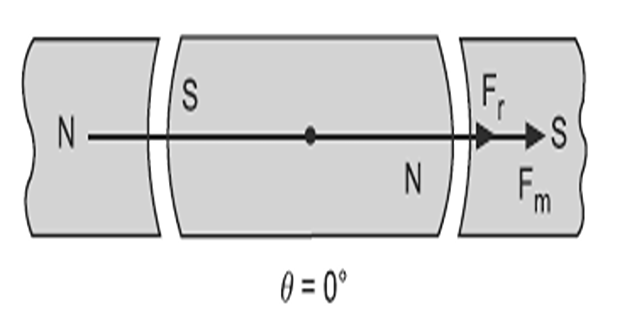
In this position, torque produced is zero because the field of rotating magnet Fr and the field of stationary permanent magnet Fm are in line with each other.

When the magnet in rotated through in angle \(\theta\left(\theta\right.\) less than \(90^{\circ},\) equal to \(90^{\circ}\) more than \(90^{\circ}\) but less than \(180^{\circ}\) ), its north pole will be attracted towards the south pole and south pole will be attracted towards the north pole of permanent stationary magnets
In other words, we can say that the rotor field \(F_{r}\) tries to come in line with main field \(F_{m}\) and torque is developed.
This anticlockwise torque is considered as negative, because it is decreasing the torque angle \(\theta\).

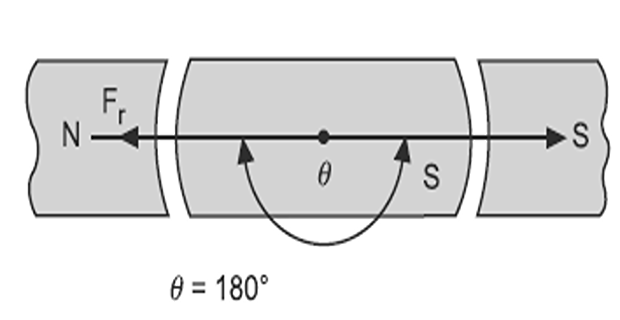
When the magnet is rotated through an angle \(\theta=180^{\circ},\) the two field \(F_{r}\) and \(F_{m}\) are in line with each other but acting in opposite direction
therefore, torque developed is zero but this is the unstable position because slight change in angle \(\theta\) in either direction will create a torque in that direction and the rotor will not regain its original position.

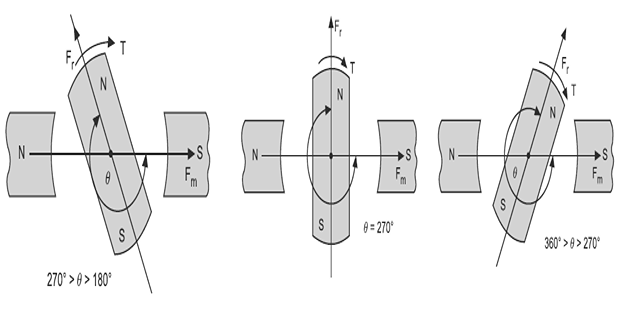
When the magnet is rotated through an angle \(\theta\) more than \(180^{\circ}\), but less than \(360^{\circ}\) (i.e., \(\theta\) is less than \(270^{\circ}\), equal to \(270^{\circ}\), more than \(270^{\circ}\) ), its north and south poles will be attracted towards the south and north poles of the permanent stationary magnets respectively
In other words, \(F_{r}\) will try to come in line with \(F_{m}\) and thus torque is developed.
This clockwise torque is considered as positive, because it is increasing the torque angle \(\theta .\)
The maximum -ve or +ve torque is produced on the rotating magnet when \(\theta=90^{\circ}\) or \(\theta=270^{\circ}\left(-90^{\circ}\right)\) respectively, because at these positions, there is maximum force of attraction or repulsion acting on magnet.

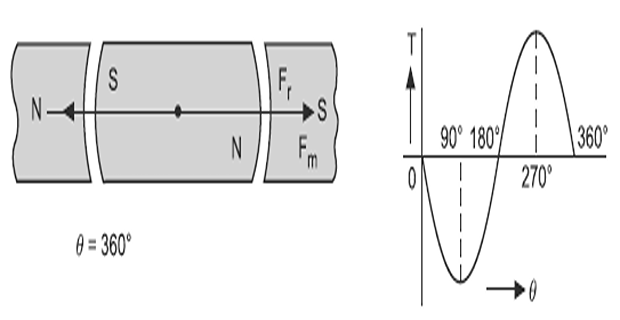
When rotating, permanent magnet is rotated through an angle \(\theta=360^{\circ},\) two field \(F_{r}\) and \(F_{m}\) are in line with each other therefore, the torque developed is zero.
This is the stable position because any change in angle \(\theta\) will develop a torque which tends to restore its original position.
Thus, it is concluded that the torque is produced due to the alignment of two fields.
The angle between the two magnetic fields on which torque depends is called Torque angle.
This torque angle is measured with respect to the direction of rotation of rotating magnet.

An electromagnet free to rotate about its axis, is placed in the magnetic field of permanent magnets.
When the field produced by the electromagnet \(F r\) is in the same direction as that of the main field produced by the stationary permanent magnets \(F m,\) the torque produced is zero
When rotated through \(\theta=90^{\circ},\) \(F_{r}\) will make \(\theta=90^{\circ}\) with \(F_{m}\).
\(F_{r}\) will try to come in line with \(F_{m}\), and produces an anticlockwise torque and is considered -ve because it reduces the torque angle \(\theta\).

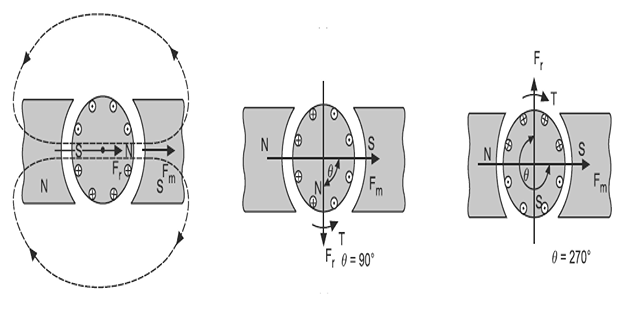
When rotated through \(\theta=270^{\circ},\) \(F_{r}\) will try to come in line with \(F_{m}\), therefore, a clockwise torque will be produced and and is considered +ve because it increases the torque angle \(\theta\).
When torque angle \(\theta\) is between zero and \(180^{\circ},\) the torque produced is -ve, whereas when \(\theta\) is between \(180^{\circ}\) to \(360^{\circ},\) the torque produced is +ve.
When \(\theta=90^{\circ}\) or \(\theta=270^{\circ}\) \(\left(-90^{\circ}\right)\), torque produced is maximum negative or maximum positive respectively.
Conclusion: variation of torque with respect to \(\theta\) is similar to that in the case of permanent rotating magnet placed in the magnetic field of permanent stationary magnet
The torque produced in this case is called an electromagnetic torque \(\left(T_{e}\right)\).