Induction Motor Model: Equivalent Circuit Breakdown | Electrical Machines

Demonstrative Video

SECTION 01

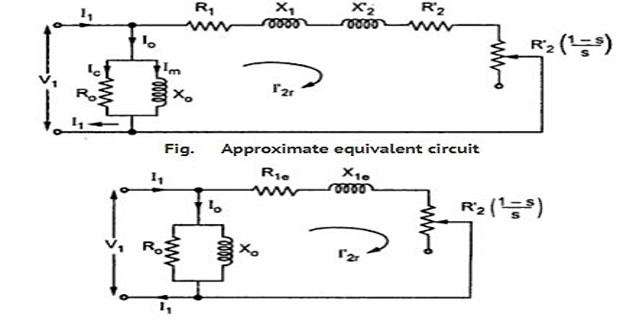
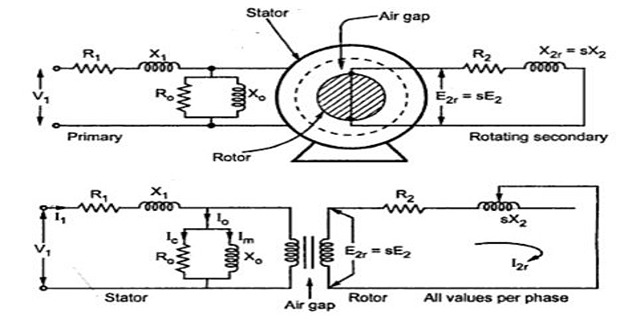
Equivalent Circuit of an IM

2-winding Transformer:
- \(I_0\) is 1% of the F.L Current
- Reason: magnetic flux is confined completely in the steel core of low reluctance, hence \(I_\mu\) is small, as a result \(I_0\) is small
Induction Motor:
- presence of air-gap (high reluctance) necessitates a large \(I_\mu\), hence \(I_0\) is very large (40-50 % of F.L Current)
Although, stator and rotor operates at different frequency, but represented in the same vector diagram because magnetic field relative to them are synchronous with each other

IM Eqckt

From above equation, rotor circuit consists of

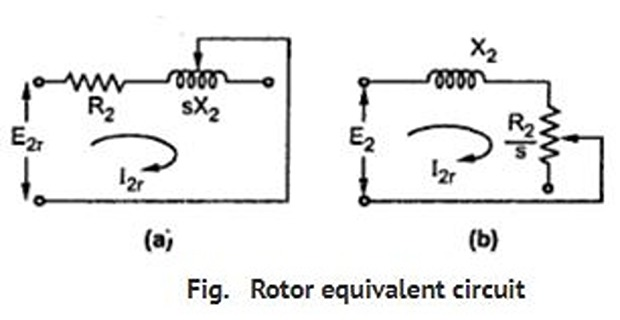
\[I_{2}=s\dfrac{E_{2}}{\sqrt{R_{2}^{2}+\left(sX_{2}\right)^{2}}}=\dfrac{E_{2}}{\sqrt{\left(R_{2}/s\right)^{2}+X_{2}^{2}}}\]
When motor is loaded, rotor current is given by
From above equation, rotor circuit consists of
- a fixed \(R_2\) and variable \(sX_2\) (proportional to slip) connected across \(E_r = sE_2\), or
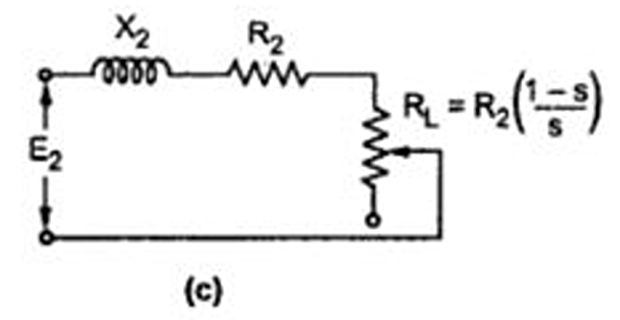
- Fixed reactance \(X_2\) connected in series with a variable \(R_2/s\) (inversely proportional to slip) and supplied with constant \(E_2\)

IM Rotor

IM Rotor1

\[\begin{aligned} \dfrac{R_{2}}{s} & =R_{2}+R_{2}\left(\dfrac{1}{s}-1\right)\\ \Rightarrow R_{2} & =\mbox{represents the rotor Cu loss}\\ \Rightarrow R_{L}&=R_{2}\left(\dfrac{1}{s}-1\right) \\ & =\mbox{electrical equivalent of the mechanical load} \end{aligned}\]

IM Ec Stator

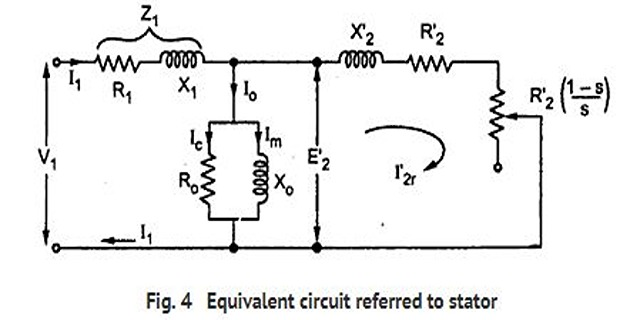
The exciting current may be transferred to the left because inaccuracy involved is negligible and calculations is very much simplified

IM Approx Ckt