Demonstrative Video
Effect of Increased Load with Constant Excitation
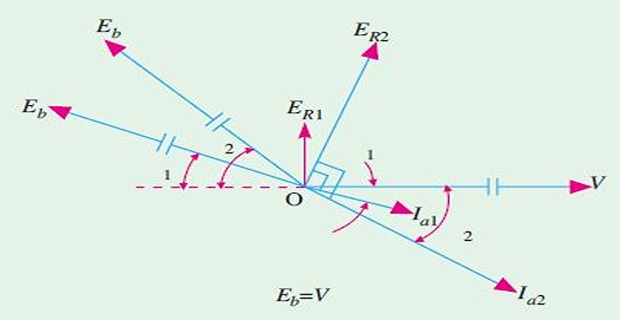
Keep excitation constant and vary the load. \(R_a << X_s\), hence phase angle between \(E_R\) and \(I_a\), i.e. \(\theta = 90^{\circ}\)
At light-load:
\(\alpha_1\) small \(\Rightarrow\) \(E_{R1}\) small \(\Rightarrow\) \(I_{a1}\) small
\(\phi_1\) small \(\Rightarrow\) \(\cos \phi_1\) large
Load increased:
motor must develop more \(T\) by drawing more \(I_a\)
unlike dc motor, syn motor cannot \(I_a \uparrow\) by \(N \downarrow\) and hence \(E_b\) because both are constants
What happens?
rotor falls back in phase i.e. \(\alpha_2 \uparrow\)
\(E_R\) increased considerably
result \(I_{a} \uparrow \Rightarrow T \uparrow\)
\(\phi \uparrow \rightarrow \cos\phi \downarrow\)
\((I_a \uparrow) >> (\cos\phi \downarrow) \Rightarrow T \uparrow\)
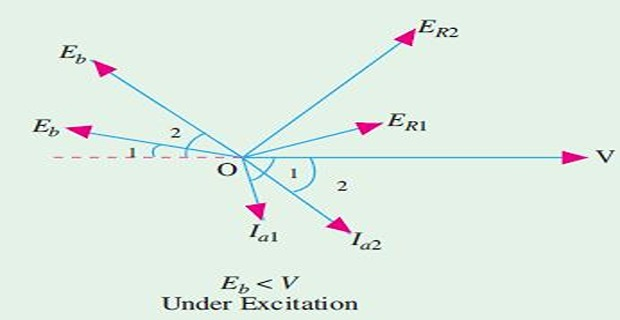
Small load \(\Rightarrow\) small \(\alpha_1\) \(\Rightarrow\) \(I_{a1}\) lags \(V\) by \(\phi_1 \uparrow\) \(\Rightarrow\) poor pf
Unlike normal excitation, \(I_a \uparrow \uparrow\) for developing same power because of poor pf
Load \(\uparrow \Rightarrow E_R \uparrow \Rightarrow I_a \uparrow \Rightarrow \phi \downarrow \Rightarrow \cos\phi \uparrow\)
Both \(I_a \uparrow\) and \(\cos\phi \uparrow\) \(\Rightarrow\) \(P_d \uparrow\) to meet the load
Change in pf is more than the change in \(I_a\)
Light load \(\Rightarrow \alpha_1\) small but \(I_{a1} \uparrow \uparrow\) and leads \(V\) by larger \(\phi_1\)
Like under-excited more load, pf improves and approaches unity
\(I_a \uparrow\) to give more power to meet the load
\(\phi \downarrow\) or pf increases at a faster rate than \(I_a\) to meet the load
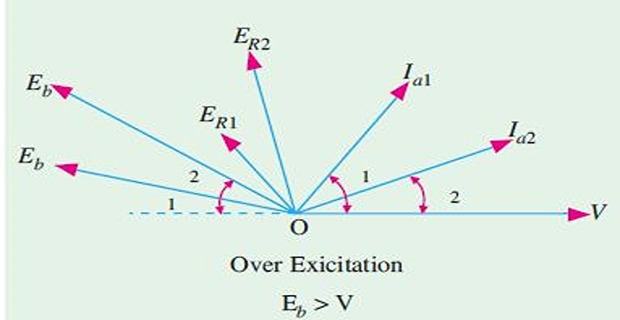
With increase in load:
For
p.f. tends to approach unity
change in p.f. is greater than \(I_a\)
With ,
change in \(I_a\) is greater than p.f. which tends to become increasingly lagging