Demonstrative Video
Effect of Excitation on Armature Current & PF
What happens under over excitation and under-excitation?
Consider SM having constant mechanical load (output constant, if losses neglected)
Case-1: \(E_b = V\) known as 100% excitation
armature \(I\) lags \(V\) by small angle \(\phi\)
\(\theta\) with \(E_R\) is fixed by stator constants i.e. \(\tan\theta=X_s/R_a\)
Case-2: \(E_b < V\) excitation is less than 100%
\(E_{R}\) advanced clockwise and so is \(I\) (because it lags behind \(E_{R}\) by fixed angle \(\theta\) ).
\(|I|\) is increased but its PF is decreased (\(\phi\) has increased).
Because input as well as \(V\) are constant, hence the power component of \(I\) i.e., \(I \cos \phi\) remains same, but watt-less component \(I\) \(\sin \phi\) is increased.
Hence, as excitation \(\downarrow\), \(I~\uparrow\) but p.f. \(\downarrow\) so that power component \(I \cos \phi=OA\) remain constant.
Locus of extremity of current vector is a straight horizontal line
Incidentally, when \(I_f~\downarrow\), the pull-out torque is also \(\downarrow\) in proportion.
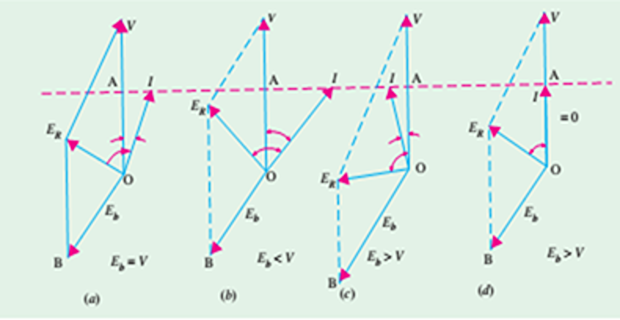
Case-3: \(E_b > V\)
\(E_{R}\) is pulled anticlockwise and so is \(I\).
Now motor is drawing a leading current.
For some value of excitation, that \(I\) may be in phase with V i.e., p.f. is unity
At that time, the current drawn by the motor would be minimum.
Two important points stand out clearly from the prevailing discussion:
\(I_a\) Vs \(I_f\)
\(|I|\) varies with excitation and has large value both for low and high values of excitation (though it is lagging for low excitation and leading for higher excitation).
In between, it has minimum value corresponding to a certain excitation.
The variations of \(I\) with excitation is known as V-curves because of their shape.
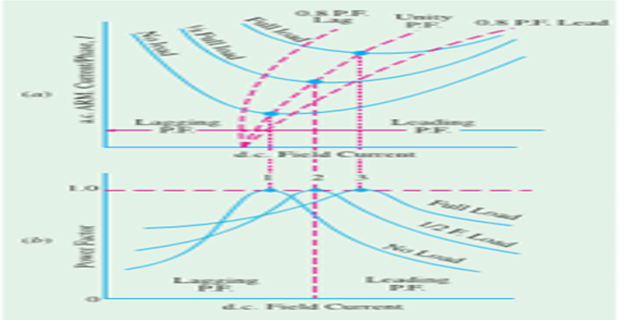
\(\cos\phi\) Vs \(I_f\)
For the same input, \(I\) varies over a wide range and so causes the power factor also to vary accordingly.
When over-excited, motor runs with leading p.f. and with lagging p.f. when under-excited. In between, the p.f. is unity.
The variations of \(p . f\). with excitation looks like inverted V-curve.