Demonstrative Video
Effect of Changing Excitation on Constant Load
Normal excitation \(\boxed{E_b=V}\) at UPF
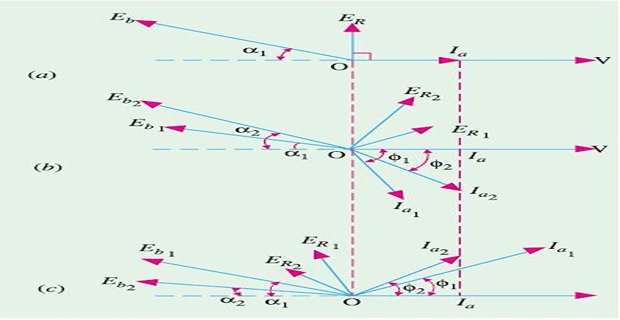
\(E_b\) is reduced to \(E_{b1}\) at same \(\alpha_1\)
\(E_{R1}\) cause lagging \(I_{a1}\)
even \(\left|I_{a1}\right| > \left|I_a\right|\) it is incapable for carrying constant load as \(VI_{a1}\cos\phi_1 < VI_a\)
hence necessary to \(\uparrow\) \((\alpha_1 \rightarrow \alpha_2)\) \(\Rightarrow\) \(\uparrow\) \((E_{b1} \rightarrow E_{b2})\) \(\Rightarrow\) \(\uparrow\) \((E_{R1} \rightarrow E_{R2}) \Rightarrow \uparrow (I_a \rightarrow I_{a2})\)
\(VI_{a2}\cos\phi_2\) meet the constant load

increased \(E_{b1}\) at original \(\alpha_1\)
\(E_{R1}\) cause leading \(I_{a1}\), whose in-phase component is larger than \(I_a\)
Hence, armature develops more power than the load
load angle decrease from \(\alpha_1\) to \(\alpha_2\) which decreases \(E_{R1}\) to \(E_{R2}\)
Consequently decrease from \(I_{a1}\) to \(I_{a2}\) whose in-phase component \(I_{a2}\cos\phi_2 = I_a\)
armature develops sufficient power to carry the constant load
Variation in excitation of a syn motor running with a given load produce variations in its load angle only.