Torque Produced in Single-Phase Induction Motors

Demonstrative Video

Torque Produced by \(1-\phi\) Induction Motor

  • Each component mmf wave induces motor action.

  • Torques from these waves oppose each other.

  • At rest, equal forward and backward flux waves yield no starting torque.

  • If these waves remain equal during rotor motion, torque-speed resembles a polyphase motor with low stator leakage impedance.

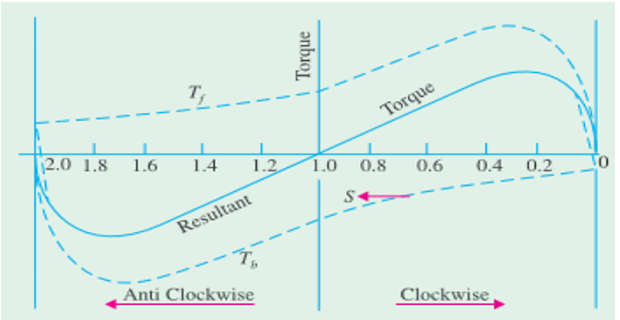
  • Resultant torque-speed characteristic is the sum of two component curves.

  • Slip varies \(0-2\)

  • At standstill, \(s=1\) and \(2-s = 1\)

  • \(T_f\) and \(T_b\) numerically equal but opposite direction

  • Hence, \(T_{st}=0\)

image

  • Motor, when started by auxiliary means, produces torque in the initiated direction.

  • Assumption of equal flux waves during rotor motion simplifies actual conditions.

  • Ignored factors: stator leakage impedance effects and Induced rotor currents not fully considered.

  • Rotor in motion increases backward rotor currents, reducing backward flux.

  • Forward field’s magnetic effect decreases as speed rises due to lower rotor currents.

  • Total flux waves remain constant, inducing a nearly constant stator counter emf.

  • Stator leakage-impedance voltage drop impact is minimized.

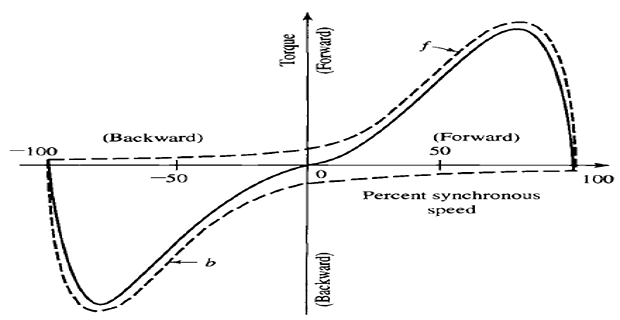
  • In motion, forward field torque surpasses backward field torque.

  • Normal running region: forward field significantly greater than backward field.
    image

  • Flux wave resembles constant-amplitude polyphase motor’s air gap.

  • Single-phase motor’s torque-speed comparable to a polyphase motor.

  • Double-stator-frequency torque pulsations result from oppositely rotating flux waves.

  • Pulsations create no average torque but contribute to motor noise.

  • Torque on curves represents the time-averaged instantaneous torque.

Rotor Slip Due to Two Rotating Fields

  • Rotor is started by axillary means and torque developed

  • Forward field: direction of initial start

  • Let \(n_s = \text{synchronous speed} \quad n = \text{rotor speed}\)

  • \[s_f = s = \dfrac{n_s-n}{n_s} = 1- \dfrac{n}{n_s}\]
    Slip of the motor w.r.t forward field
  • \[s_b = \dfrac{n_s-(-n)}{n_s} = 1+ \dfrac{n}{n_s}\]
    Backward rotating flux rotates opposite to the stator, thus the corresponding back slip
  • \[s_f + s_b = 2~\quad \Rightarrow~s_b = \left(2-s_f\right)\]
    Adding both slips:

Making Single-Phase IM Self-Starting

  • Motor is temporarily converted into a two-phase motor for self-starting.

  • Stator has an additional starting winding alongside the main winding.
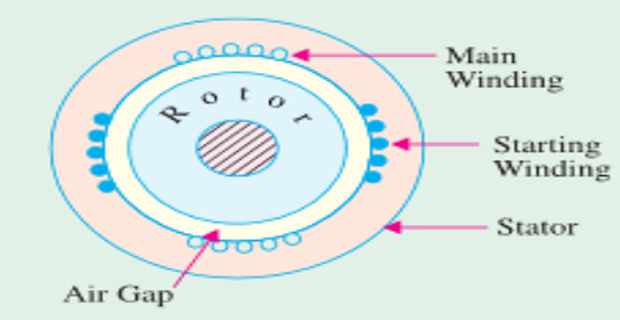
    image

  • Two windings, spaced electrically \(90^{\circ}\) apart, are connected in parallel to a single-phase supply.

  • Ideal phase difference between the stator winding currents is \(90^{\circ}\).

  • The resulting currents create a revolving flux, ensuring self-starting of the motor.