Demonstrative Video
Equivalent Circuit
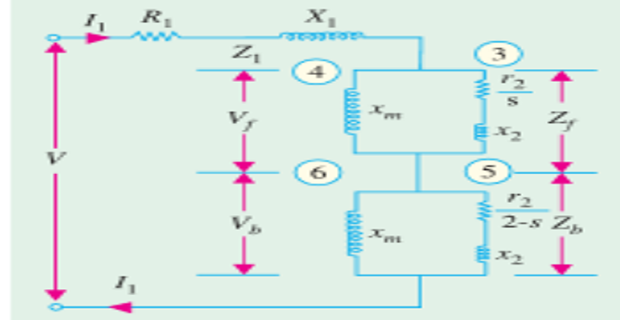
Single-phase motor conceptualized as single common stator winding, but two rotors revolving in opposite directions.
Equivalent circuit based on double-field revolving theory
Without Core Loss
The stator impedance: \(Z_1 = R_1 + j X_1\)
Each rotor impedance: \(r_2 + jx_2\)
\(r_2\) (rotor resistance), \(x_2\) (standstill reactance), and \(x_m\) (magnetising reactance) are half the actual values w.r.t stator (as referred to stator)
Iron loss neglected so exciting branch has only \(x_m\)
Full values by capital letters and half-values by small letters
- \[Z_f = \dfrac{jx_m\left(\dfrac{r_2}{s}+jx_2\right)}{\dfrac{r_2}{s}+j\left(x_m+x_2\right)}\]Impedance of forward running motor with
- \[Z_b = \dfrac{jx_m\left(\dfrac{r_2}{2-s}+jx_2\right)}{\dfrac{r_2}{2-s}+j\left(x_m+x_2\right)}\]Impedance of backward running motor with

Under standstill condition, \(V_f = V_b\)
Under running condition, \(V_f\) almost \(90-95\%\) of \(V\)
- \[P_g = \left(\dfrac{1-s}{s}\right) \cdot I_2^2R_2\]Power developed by the rotor :
- \[T_g = \dfrac{1}{2\pi N} \left(\dfrac{1-s}{s}\right) \cdot I_2^2R_2\]is the rotor r.p.s, then torque is If
- \[T_g = \dfrac{1}{2\pi N_s} \dfrac{I_2^2R_2}{s} = k \cdot \dfrac{I_2^2R_2}{s}\], then Since
- \[T_f = K \cdot \dfrac{I_2^2R_2}{s} \qquad T_b = -K \cdot \dfrac{I_2^2R_2}{(2-s)}\]Therefore, forward and backward torques are:
Total torque \(T=T_f+T_b\)
- \[T_f = I_3^2\cdot r_2/s\]Forward torque in synchronous watts:
- \[T_b = I_5^2 \cdot r_2/(2-s)\]Backward torque :
- \[T = T_f - T_b\]Total torque:
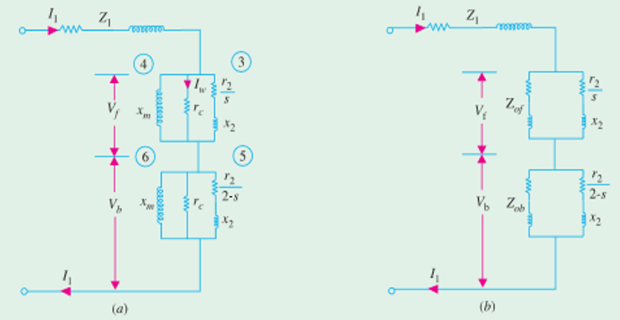
core loss represented by \(r_c\) connected in parallel with \(x_m\)
Running condition: \(V_f >> V_b\)
Most of the iron-loss take place in forward motor \(I_w = P_i/V_f\)

Advantages & Limitations
Advantages:
smaller in size and lighter in weight
cheaper in cost
highly efficient
requires less maintenance
have a longer life
can be designed in a variety of sizes
Limitations
For a given frame size and temperature, its output is only 50% of the three-phase induction motor
Not self-started
Have a lower power factor
Efficiency is lower
Do not have a starting torque
For the same power output, these motors are more expensive than three-phase induction motors.