Demonstrative Video
Ampere-turns Calculations
\[\phi=\frac{\text { m.m.f. }}{\text { reluctance
}}=\frac{N I}{l / a \mu_{0} \mu_{r}}\]
\[\text { AT required, } N I=\frac{\phi l}{a
\mu_{0} \mu_{r}}=\frac{B}{\mu_{0} \mu_{r}} l=H l\]
In a magnetic circuit, flux produced,
Series Magnetic Circuits
In series magnetic circuit without air-gap \(NI=\Phi\Re=Hl\)
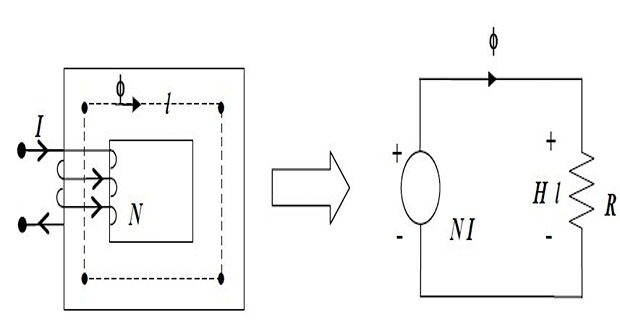
It is a series circuit so same flux (\(\Phi\)) flows through the two medium- iron and air

Total reluctance \(\Re = \Re_{iron} + \Re_{air}\)
- \[\begin{aligned} H_{i} & =\dfrac{B}{\mu_{0}\mu_{i}}\\ H_{g} & =\dfrac{B}{\mu_{0}}\\ \therefore\Phi & =\dfrac{NI}{\left(\Re_{i}+\Re_{g}\right)} \end{aligned}\]too will be different Since value of permeabilities are different for iron and air, the corresponding values of
Series-Parallel magnetic circuit
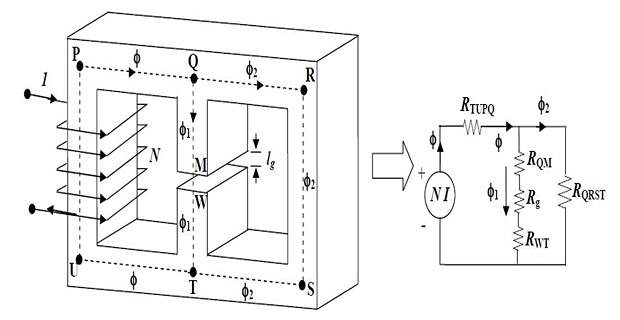

\[\begin{aligned}
\Phi & =\Phi_{1}+\Phi_{2}\\
NI &
=Hl+H_{1}l_{1}+H_{g}l_{g}=\Re\Phi+\left(\Re_{1}+\Re_{g}\right)\Phi_{1}\\
\left(\Re_{1}+\Re_{g}\right)\Phi_{1} & =\Re_{2}\Phi_{2}\\
H_{1}l_{1}+H_{g}l_{g} & =H_{2}l_{2}\\
NI & =Hl+H_{2}l_{2}
\end{aligned}\]