Demonstrative Video
Review of Symbols
| Terms | Symbols | Units |
|---|---|---|
| Flux Density | \(B\) | Tesla (\(T\)) |
| Flux | \(\Phi\) | Webers (\(Wb\)) |
| Flux Linkage | \(\lambda\) | Volt-seconds (\(V-s,Wb-t\)) |
| Current | \(i\) | Amperes (\(A\)) |
| Field Intensity | \(H\) | Ampere/meters (\(A/m\)) |
| Permeability | \(\mu\) | Henries/meter \((H/m)\) |
| mmf | \(F\) | Ampere-turns (\(A-t\)) |
| Permeance | \(P\) | Henries (\(H\)) |
| Reluctance | \(R\) | inverse Henries (\(1/H\)) |
| Inductance | \(L\) | Henries (\(H\)) |
| Current (fields) into page | \(\otimes\) | |
| Current (fields) out of page | \(\odot\) |
Magnetic & Electrical Circuit Analogy
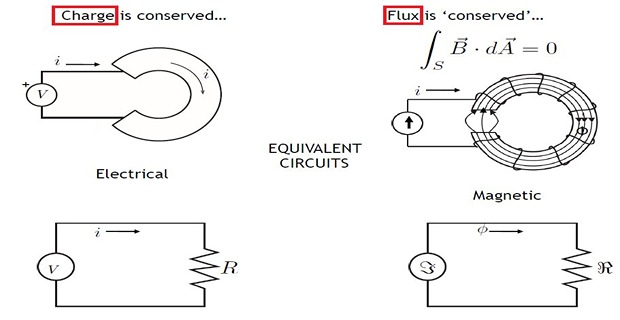
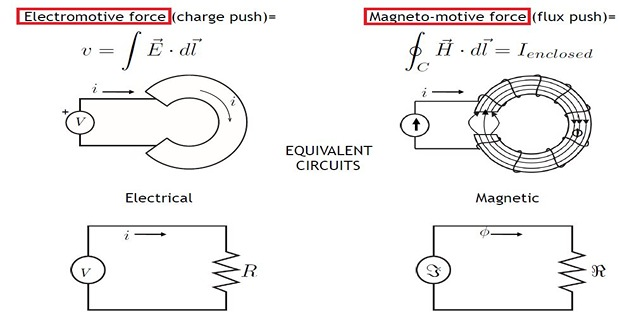
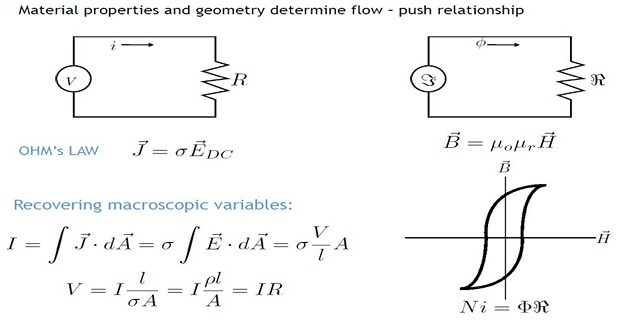
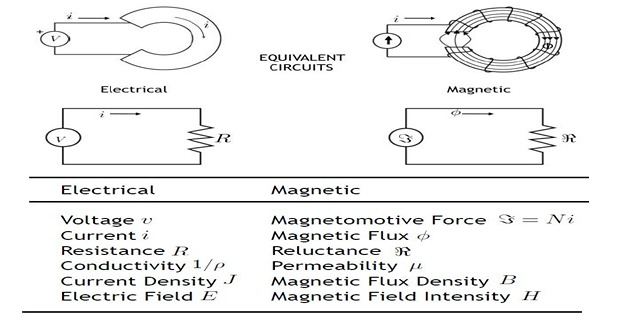
Dissimilarities: Magnetic & Electric Circuit
Magnetic flux does not flow but it sets up in the magnetic circuit (basically molecular poles are aligned)
The electric current (electrons) actually flows in an electric circuit
For magnetic flux, there is no perfect insulator. It can be set-up even in the non-magnetic materials like air, rubber, glass etc. with reasonable mmf
For electric current, there are large number of perfect insulators like glass, air, rubber, etc., which do not allow it to follow through them under normal conditions.
Reluctance of a magnetic circuit is not constant rather it varies with the value of \(B\) because \(\mu_r\) changes considerably with the change in \(B\)
The resistance of an electric circuit is almost constant as its value depends upon the value of \(\rho\) which is almost constant. However, the value of \(\rho\) and \(R\) may vary slightly if temperature changes
Once the magnetic flux is set-up in a magnetic circuit, no energy is expanded. However, a small amount of energy is required at the start to create flux in the circuit.
Energy is expanded continuously, so long as the current flows through an electric circuit. This energy is dissipated in the form of heat.