Demonstrative Video
- Gross-Mechanical Power Developed:
\[\begin{aligned}
P_{m} & =P_{2}-P_{c}\\
&
=\dfrac{3\left(I_{2r}^{'}\right)^{2}R_{2}^{'}}{s}-3\left(I_{2r}^{'}\right)^{2}R_{2}^{'}\\
&
=3\left(I_{2r}^{'}\right)^{2}R_{2}^{'}\left(\dfrac{1-s}{s}\right)
\end{aligned}\]
- Torque Developed:
\[\begin{aligned}
T &
=\dfrac{P_{m}}{\omega}=\dfrac{3\left(I_{2r}^{'}\right)^{2}R_{2}^{'}\left(\dfrac{1-s}{s}\right)}{\dfrac{2\pi
N}{60}}\\
&
=\dfrac{3\left(I_{2r}^{'}\right)^{2}R_{2}^{'}\left(\dfrac{1-s}{s}\right)}{\dfrac{2\pi
N_{s}\left(1-s\right)}{60}} \\
&
=9.55\times\dfrac{\dfrac{3\left(I_{2r}^{'}\right)^{2}R_{2}^{'}}{s}}{N_{s}}
\end{aligned}\]
- Maximum Power Output:
On further simplifying the approximate equivalent circuit
exciting circuit is omitted i.e. \(I_0\) is neglected
\(K\) is assumed unity
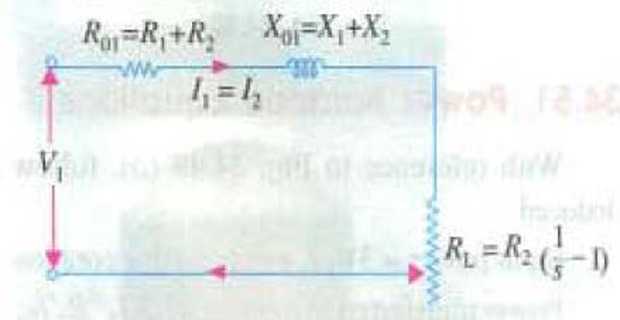
- \[\begin{aligned} P_{g} & =3I_{1}^{2}R_{L}\\ & =3\left[\dfrac{V_{1}}{\sqrt{\left(R_{01}+R_{L}\right)^{2}+X_{01}^{2}}}\right]^{2}R_{L}\\ & =\dfrac{3V_{1}^{2}R_{L}}{\left(R_{01}+R_{L}\right)^{2}+X_{01}^{2}} \end{aligned}\]Gross-power is given by
- \[\begin{aligned} R_{L}^{2} & =R_{01}^{2}+X_{01}^{2}\\ & =Z_{01}^{2}\\ \Rightarrow R_{L} & =Z_{01} \end{aligned}\]The condition for maximum power output is obtained by differentiating and equating with zero, we get
Hence, power is maximum when the equivalent load resistance is equal to the standstill leakage impedance of the motor
Corresponding slip:
\[\begin{aligned}
Z_{01} & =R_{L}=R_{2}\left[\left(1/s\right)-1\right]\\
& \Rightarrow s=\dfrac{R_{2}}{R_{2}+Z_{01}}\\
P_{m,max} &
=\dfrac{3V_{1}^{2}Z_{01}}{\left(R_{01}+Z_{01}\right)^{2}+X_{01}^{2}}\\
& =\dfrac{3V_{1}^{2}}{2\left(R_{01}+Z_{01}\right)}
\end{aligned}\]
is unity is volt/phase and NOTE: