Inductance: Understanding Self & Mutual Inductance | Electrical Machines

Demonstrative Video

SECTION 01

Self Inductance

The property of a coil due to which it opposes the change of current flowing through itself is called self inductance or inductance of the coil
This property (i.e., inductance) is attained by a coil due to self-induced emf produced in the coil itself by the changing current flowing through it.
If \(I\) in the coil is increasing (by the change in circuit conditions), the self-induced emf is produced in the coil in such a direction so as to oppose the rise of current i.e., the direction of self-induced emf is opposite to that of the applied voltage.
On the other hand, if \(I\) in the coil is decreasing, the self-induced emf is produced in the coil in such direction so as to oppose the fall of current i.e., the direction of self-induced emf is in the same direction as that of the applied voltage.

Key Concepts

In fact, self-inductance does not prevent the change of current but it delays the change of current flowing through a coil.
It may be noted that this property of the coil only opposes the changing current (i.e., alternating current).
However, it does not affect the steady (i.e., direct) current when flows through it.
In other words, the self-inductance of the coil (by virtue of its geometrical and magnetic properties) will exhibit its presence to AC but it will not exhibit its presence to DC

\[\begin{aligned} L &=\frac{e}{d I / d t}\left(\text { since } e=L \frac{d I}{d t}\right) \\ &=\frac{N \phi}{I}\left(\text { since } e=N \frac{d \phi}{d t}=L \frac{d I}{d t}\right)\\ &=\frac{N^{2}}{l / a \mu_{0} \mu_{r}}\left(\text { since } \phi=\frac{N I}{l / a \mu_{0} \mu_{r}}\right) \end{aligned}\]

SECTION 02

Mutual Inductance

The property of one coil due to which it opposes the change of current in the other (neighbouring) coil is called mutual-inductance between the two coils
This property (i.e., mutual-inductance) is attained by a coil due to mutually induced emf in the coil while current in the neighbouring coil is changing

\[\begin{aligned} M &=\frac{e_{m}}{d I_{1} / d t}\left(\text { since } e_{m}=M \frac{d I_{1}}{d t}\right) \\ &=\frac{N_{2} \phi_{12}}{I_{1}}\left(\text { since } e_{m}=N_{2} \frac{d \phi_{12}}{d t}=M \frac{d I_{1}}{d t}\right) \\ &=\frac{N_{1} N_{2}}{l / a \mu_{0} \mu_{r}}\left(\text { since } \phi_{12}=\frac{N_{1} I_{1}}{l / a \mu_{0} \mu_{r}}\right) \end{aligned}\]

SECTION 03

Co-efficient of Coupling

When current flows through one coil, it produces flux (\(\phi_1\)).
The whole \(\phi\) may not be linking with the other coil coupled to it.

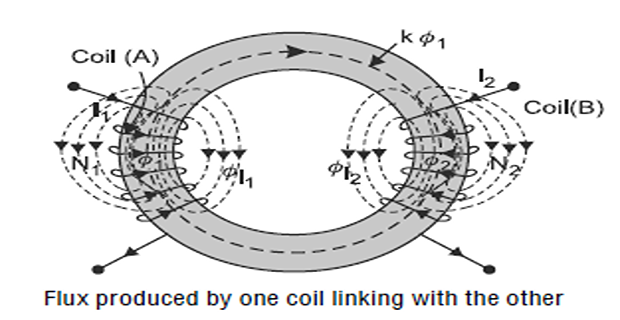
It may be reduced, because of leakage flux (\(\phi_l\)), by a fraction k known as co-efficient of coupling
Thus, the fraction of \(\phi\) produced by \(I\) in one coil that links with the other is known as co-efficient of coupling (k)
If \(\phi\) produced by one coil completely links with the other, then the value of k is one and the coils are said to be magnetically tightly coupled.
Whereas, if \(\phi\) produced by one coil does not link at all with the other, then the value of k is zero and the coils are said to be magnetically isolated

Key Concepts

\[L_{1}=\frac{N_{1} \phi_{1}}{I_{1}} \text { and } M=\frac{N_{2} \phi_{12}}{I_{1}}=\frac{N_{2} k \phi_{1}}{I_{1}} \quad \ldots(i)\left(\because \phi_{12}=k \phi_{1}\right)\]

Or Multiplying equation (i) and (ii), we get, Or Now considering coil- 2 carrying current