Transformer Basics: Ideal Transformers & The EMF Equation

Ideal Transformer

• An ideal transformer is one which has no losses, i.e. its windings have no ohmic resistance, there is no magnetic leakage, and hence has no \(I^2R\) and core losses

• In other words, an ideal transformer consists of two purely inductive coils wound on a loss-free core

• It is impossible to realize such a transformer in practice

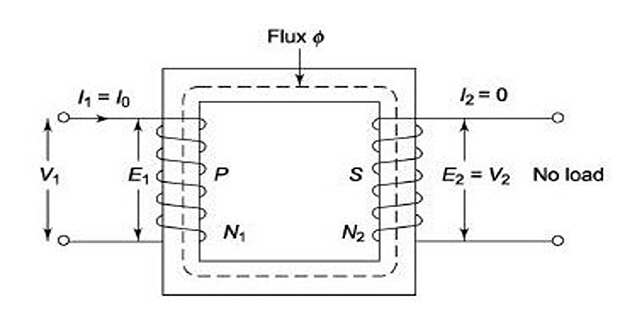
• Consider an ideal transformer whose secondary is open and primary is connected to sinusoidal alternating voltage \(V_1\)

• Potential difference cause an alternating current to flow in the primary

• Since, the primary coil is purely inductive and the secondary is open (no output) the primary draws a magnetizing current \(I_\mu\) only

• \(I_\mu\) is very small in magnitude, magnetize the core, and lags \(V_1\) by \(90^0\)

• The alternating current \(I_\mu\) produces an alternating flux \(\Phi\), which at all times is proportional to the current and is in phase with it.

  

• This changing flux is linked with both \(N_1\) and \(N_2\)

• Therefore, it produced self induced emf in the primary (\(E_1\)) which at every instant oppose \(V_1\) known as counter emf or back emf of the primary

• Similarly, there is secondary mutually induced emf (\(E_2\)), antiphase with \(V_1\)

• The magnitude of \(E_2\) is proportional to the rate of change of flux and the number of secondary turns

EMF Equation of a transformer

Let,

Voltage Transformation Ratio

\[\dfrac{E_{2}}{E_{1}}=\dfrac{N_{2}}{N_{1}}=K\] Step-Up Transformer: \[N_{2}>N_{1}\Rightarrow K>1\]

Step-Down Transformer: \[N_{2}<N_{1}\Rightarrow K<1\]

For an ideal transformer, input VA = output VA \[\begin{aligned} V_{1}I_{1} & =V_{2}I_{2}\\ \Rightarrow\dfrac{I_{2}}{I_{1}} & =\dfrac{V_{1}}{V_{2}}=\dfrac{1}{K} \end{aligned}\] Currents is in inverse proportional of the voltage transformation ratio