Tame the Currents Within: Understanding Eddy Current Loss

When a magnetic material is subjected to ac magnetic field, an emf is induced in itself according to Faraday’s laws of electro-magnetic induction.
Since the magnetic material is also conducting, these emfs circulate currents within the body
These circulating currents are known as eddy currents.
As these currents are not used for doing any useful work, therefore, these currents produce a loss (\(I^2R\) loss) called eddy current loss.
Like hysteresis loss, this also increases the temperature
The hysteresis and eddy current losses in a magnetic material are called iron losses or core losses or magnetic losses.

Eddy currents produce eddy current loss \(I^2R\), where \(I\) is the value of eddy currents and \(R\) is resistance of eddy current path.
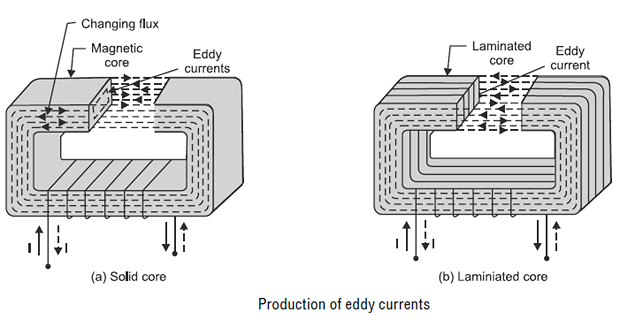
As the core is a continuous iron block of large cross-section, the magnitude of \(I\) will be very large and hence greater eddy current loss will result.

To reduce the eddy current loss, the obvious method is to reduce magnitude of eddy currents.
This can be achieved by splitting the solid core into thin sheets (called laminations) in the planes parallel to the magnetic field
Each lamination is insulated from the other by a fine layer of insulation (varnish or oxide film).
This arrangement reduces the area of each section and hence the induced emf
It also increases the resistance of eddy currents path since the area through which the currents can pass is smaller.
This loss can further be reduced by using a magnetic material having higher value of resistivity (like silicon steel).

When the affects of eddy currents (production on heat) are not utilised, the power or energy consumed by these currents is known as eddy current loss.
There are places where eddy currents are used to do some useful work e.g., in Induction heating.
In this case, an iron shaft is placed as a core of an inductive coil.
When high frequency current is passed through the coil, a large amount of heat is produced at the outer most periphery of the shaft by \(I_{\text{eddy}}\).
The amount of heat reduces considerably when we move towards the centre of the shaft.

This is because outer periphery of the shaft offers low resistance path to \(I_{\text{eddy}}\)
This process is used for surface hardening of heavy shafts like axils of automobiles.
\(I_{\text{eddy}}\) effects are also used in electrical instrument e.g., providing damping torque in permanent magnet moving coil instruments and braking torque in case of induction type energy meters.

Although it is difficult to determine the eddy current power loss from the current and resistance values.
However, experiments reveal that the eddy current power loss in a magnetic material can be expressed as: \[P_{e}=K_{e} B_{m}^{2} t^{2} f^{2} V \text { watt }\] where, \(K_{e}=\) co-efficient of eddy current, its value depends upon the nature of magnetic material; \[\begin{aligned} B_{m} &=\text { maximum value of flux density in } \mathrm{Wb} / \mathrm{m}^{2} \\ t &=\text { thickness of lamination in } \mathrm{m} \\ f&= \text{frequency of reversal of magnetic field in Hz}\\ V&= \text{volume of magnetic material in} \mathrm{m}^{3} \end{aligned}\]