Armature Reaction & Compensation

Demonstrative Video

Armature Reaction

  • Effect of magnetic field set up by armature current on the distribution of flux under the main poles

  • Effect of armature magnetic field:

    • Demagnetizes or weakens the main flux
      : leads to reduced generated voltage

    • Cross-magnetizes or distorts it
      : leads to sparking at the brushes

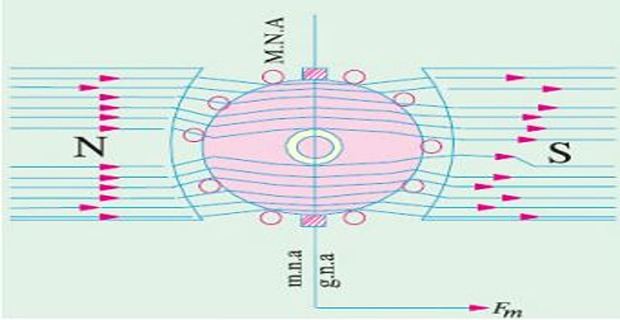
image

    Main field alone

  • The flux is distributed symmetrically w.r.t. the polar axis

  • The Magnetic Neutral Axis (MNA), axis along which no emf is produced in the armature conductors because they move parallel to the line of flux.

  • MNA axis is \(\perp\) to the flux passing through armature

  • MNA also called "axis of commutation" because reversal of current in armature conductors take place across this axis

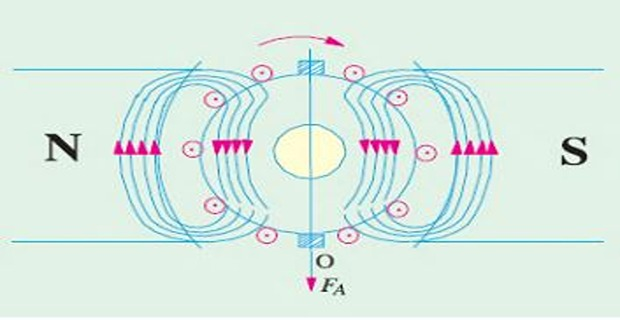
image

Armature field alone

  • Flux set up by \(I_a\) alone field coils being unexcited

  • The mmf of the armature conductors combine to send flux downwards through the armature shown by vector \(OF_A\)

Both fields together

Under actual condition, both the mmfs (main and armature) exist simultaneously

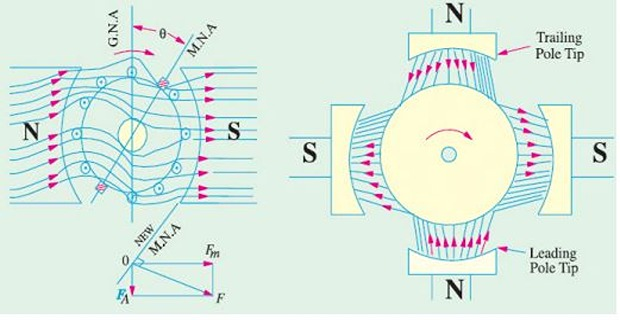
image

  • Flux through armature is no longer uniform and symmetrical rather it is distorted

  • Flux is crowded at the trailing pole tips but weakened or thinned out at the leading pole tips (the pole tip which is first met during rotation by armature conductors is known as leading pole tip and the other as trailing pole tip)

  • \(\overrightarrow{OF}=\overrightarrow{OF_{M}}+\overrightarrow{OF_{A}}\)

  • The new position of MNA, which is always \(\perp\) to resultant mmf \(OF\)

  • With the shift of MNA by \(\theta\), brush also shifts, to lie in the new position of MNA

  • Due to brush shift (forward lead), \(I_a\) redistribution occurs, earlier which were under the influence of \(N\)-pole comes under the influence of \(S\)-pole, and vice versa

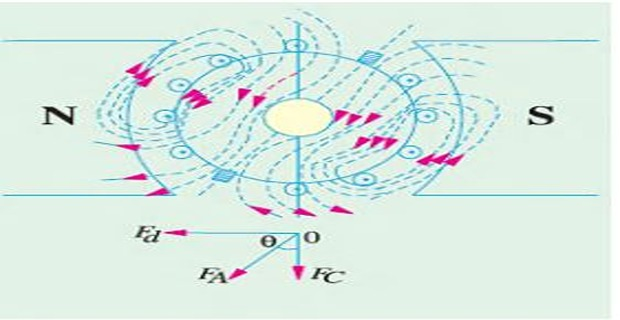
image

  • The armature mmf \(OF_A\) lie in the direction of the new position of MNA (or brush axis)

  • \(OF_A\) is not vertical but inclined by an angle \(\theta\)

  • \(OF_A\) resolved as \(OF_d\) (parallel to polar axis) and \(OF_c\) (\(\perp\) to the axis)

De-magnetizing and Cross-magnetizing

  1. Component \(OF_c\) right angle to \(OF_m\) (representing the main mmf) produces distortion in the main field and hence called the or distorting component of the armature reaction

  2. Component \(OF_d\) is in direct opposition of \(OF_m\) exerts a demagnetizing influence on the main pole flux called the or weakening component of the armature reaction

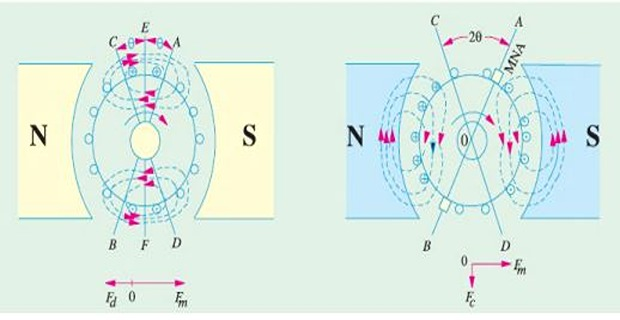
image

De-magnetizing AT per Pole

\[\begin{aligned} Z & =\mbox{total number of armature conductors}\\ I & =\mbox{current in each armature conductor}\\ & =I_{a}/2\cdots\cdots\mbox{for wave winding}\\ & =I_{a}/P\cdots\cdots\mbox{for lap winding}\\ \theta_{m} & =\mbox{forward lead in mechanical degrees} \end{aligned}\]
is and No. of armature cond. in
\[\begin{aligned} \mbox{Total no. of turns in these angles} & =\dfrac{2\theta_{m}}{360}\times Z\\ \mbox{Demagnetising amp-turns per pair of poles} & =\dfrac{2\theta_{m}}{360}\times ZI\\ AT_{d}\mbox{ per pole} & =\boxed{ZI\times\dfrac{\theta_{m}}{360}} \end{aligned}\]
As two conductors constitute one turn

Cross-magnetizing AT per Pole

Cross-magnetizing conductors lie between \(\angle AOD\) and \(BOC\)

\[\begin{aligned} \mbox{Demagnetizing conductors/pole} & =Z\dfrac{2\theta_{m}}{360}~\left(\mbox{already found}\right)\\ \mbox{Cross-magnetising conductors/pole} & =\dfrac{Z}{P}-Z\times\dfrac{2\theta_{m}}{360}\\ & =Z\left(\dfrac{1}{P}-\dfrac{2\theta_{m}}{360}\right)\\ \mbox{Cross-magnetizing amp-conductors/pole} & =ZI\left(\dfrac{1}{P}-\dfrac{2\theta_{m}}{360}\right)\\ \mbox{Cross-magnetizing amp-turns/pole} & =ZI\left(\dfrac{1}{2P}-\dfrac{2\theta_{m}}{360}\right)\\ & \left(\mbox{2 cond. = 1 turn}\right)\\ AT_{c}/\mbox{pole} & =\boxed{ZI\left(\dfrac{1}{2P}-\dfrac{\theta_{m}}{360}\right)} \end{aligned}\]
Total armature-cond./pole for both cross and demag. =
NOTE:
  1. \[\begin{aligned} \mbox{No. of extra turns/pole} & = \dfrac{AT_d}{I_{sh}} \cdots \mbox{for shunt generator} \\ & = \dfrac{AT_d}{I_{a}} \cdots \mbox{for series generator} \\ \end{aligned}\]
    For neutralizing demagnetizing effect an extra number of turns may be put on each pole
  2. \[\begin{aligned} \theta (\mbox{mechanical}) & = \dfrac{\theta (\mbox{electrical})}{\mbox{pair of poles}}\\ \theta_m & = \dfrac{\theta_e}{P/2} \end{aligned}\]
    If lead angle is given in electrical degrees, it should be converted into mechanical degrees by using

Compensating Windings

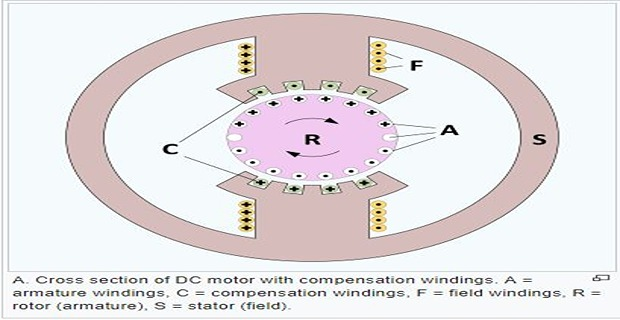
image

Embedded in pole shoes slots, connected in series with armature such that the current in them flows in opposite direction to that flowing in armature conductors directly below the pole shoes

  • Used for large dc machines subjected to large fluctuations in load, e.g. rolling mill motors and turbo-generators, etc.

  • To neutralize the cross-magnetizing effect of armature reaction

  • Absence of compensating winding result sudden shifting of flux forward and backward with every change in load

  • Shifting of flux will cause statically induced emf in the armature coils, whose magnitude depend upon the rapidity of change in load and the amount of change

  • \[\begin{aligned} Z_{c}I_{a} & =Z_{a}\left(I_{a}/A\right)\\ \Rightarrow Z_{c} & =Z_{a}/A \end{aligned}\]
    Compensating winding provides sufficient mmf to counterbalance the armature mmf

No. of Compensating Winding

\[\begin{aligned} \mbox{No. of armature cond./pole} \\ =Z/P & \\ \mbox{No. of armature turns/pole} \\ =Z/2P & \\ \mbox{No. of armature-turns immediately under one pole}\\ = \dfrac{Z}{2P}\times\dfrac{\mbox{Pole arc}}{\mbox{Pole pitch}} & \\ = 0.7\times\dfrac{Z}{2P} & \\ \mbox{No. of armature amp-turns/pole for compensating winding}\\ = 0.7\times\dfrac{Z}{2P} & \\ = 0.7\times\mbox{armature amp-turns/pole} & \end{aligned}\]