Demonstrative Video
Factors Affecting Alternator Size
Efficiency increases as power increases
1 KW \(\Rightarrow \eta = 50\%\) whereas 10 MW \(\Rightarrow \eta = 90\%\)
1000 MW and above \(\Rightarrow \eta = 99\%\)
power output per kilogram increases as power increases
1 KW weighs 20 Kg (i.e. 50 W/Kg), then, 10 MW weighing 20,000 Kg yield 500 W/Kg
Conclusion: Larger alternator weigh relatively less than smaller ones and are consequently cheaper
As size increases cooling problem (high power loss per unit surface area)
Effective cooling system (cost increases, sets upper limit)
50 MW (cold air), 50-300 MW (Hydrogen cooling), 1000 MW (hollow water-cooled conductors)
Low speed alternator are bigger than high speed alternators of the same power
Alternator on Load
\(\checkmark\) Like dc gen, as , also varies, due to the following :
voltage drop/phase \(I_aR_a\) in phase with \(I_a\)
practically negligible
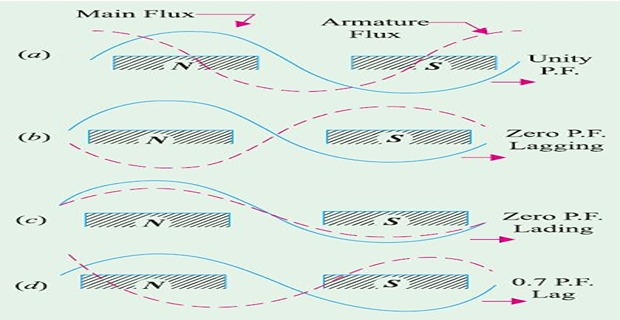
\(\Phi\) setup by \(I_a\) do not cross the air-gap but take different paths, known as
\(\Phi_L\) independent of saturation but dependent on \(I_a\)
\(\Phi_L\) sets up reactance emf which is ahead of \(I\) by \(90^{\circ}\)
of the load has a considerable effect on the armature reaction
Combined MMF wave is sinusoidal which
moves synchronously, fixed relative to the poles,
amplitude \(\propto\) load current,
position depends on p.f. of the load
, less emf
field excitation need to be increased to compensate the weakening
, more emf
field excitation need to be reduced
partly distortional and partly demagnetising
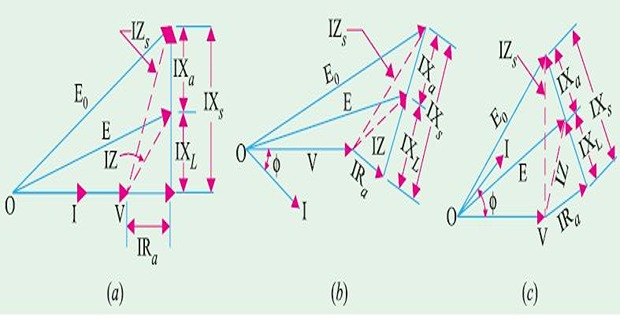
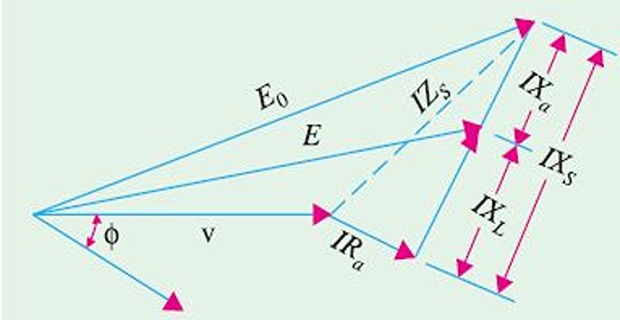
- \[X_s = X_L+X_a^{\ast}\]varies with the p.f. the load because armature reaction depends on load p.f. The ohmic value of
- \[Z_s=R_a+jX_s\]
For different loading: