Speed Control of DC Motors

Speed Control of DC Motors \[\boxed{N \propto \dfrac{E_b}{\Phi} \propto \dfrac{V-I_aR_a}{\Phi}}\] By varying:

• \(R_a\): Armature Resistance or Rheostatic Control

• \(\Phi\): Field Flux Control

• \(V\): Variation in applied voltage

Armature Resistance Control

Shunt Motor

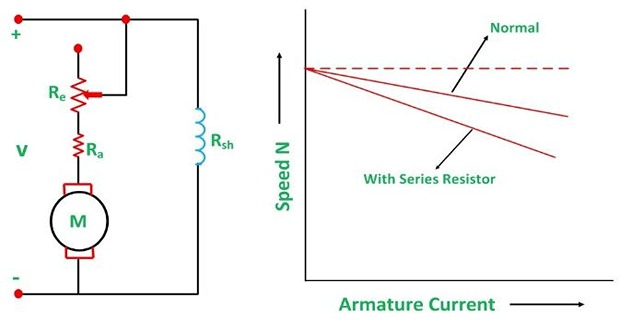
The variation in the variable resistance does not effect the flux as the field is directly connected to the supply mains.

Series Motor

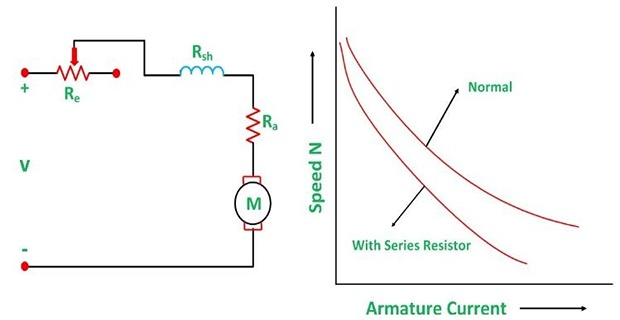
By varying \(R_a\), the \(I\) and \(\Phi\) both are affected. The voltage drop in the variable resistance \(V \downarrow\) to the armature, and as a result, the \(N \downarrow\).

When \(R_e \uparrow\), the motor runs at a lower speed. Since the variable resistance carries full armature current, it must be designed to carry continuously the full armature current.

Disadvantages of Armature Resistance Control Method

• A large amount of power is wasted in the external resistance

• Restricted to keep the speed below the normal speed of the motor and increase in the speed above normal level is not possible by this method.

• For a given value of variable resistance, the speed reduction is not constant but varies with the motor load.

• used only for small motors

Field Flux Control

Shunt Motor

\[\begin{aligned} I_{sh} & = \dfrac{V}{R_{sh}+R_c} & R_c = \mbox{shunt field regulator} \end{aligned}\] \(R_c \Rightarrow I_f \downarrow \Rightarrow \Phi \downarrow \Rightarrow N \uparrow \Rightarrow\) motor runs \(>\) normal speed

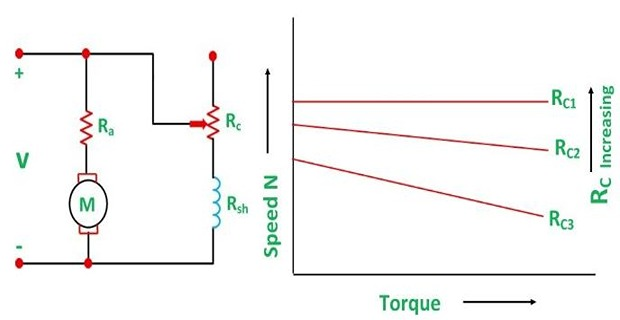
Method is used to correct the fall of speed because of load

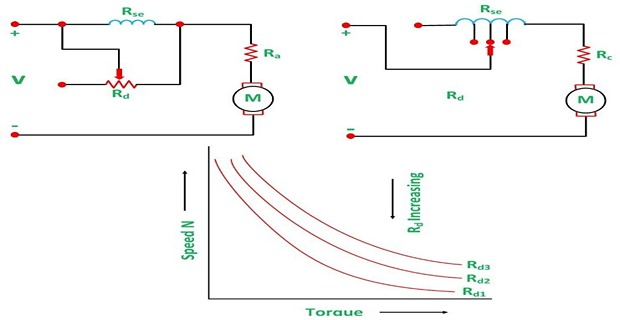
Series Motor:

: By using a Diverter (\(I_f \downarrow \Rightarrow \Phi \downarrow \Rightarrow N \uparrow\)) or Tapped field control (ampere-turns is varied by varying \(N_{se}\))

Advantages of Field Flux Control

• This method is easy and convenient.

• As the shunt field is very small, the power loss in the shunt field is also small.

1. Flux cannot be increased beyond its normal values because of the saturation of the iron

2. Therefore, speed control by flux is limited to the weakening of the field, which gives an increase in speed.

3. Applicable over only to a limited range because if the field is weakened too much, there is a loss of stability.

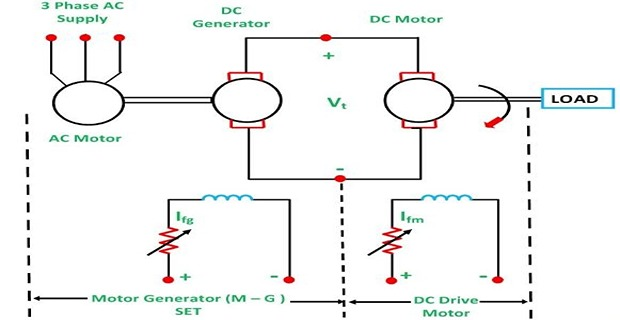
Variation in applied voltage

This speed control method is also known as Ward Leonard Method